Комментарии к задаче №4
§18. Случайные величины непрерывного типа.
Если
возможные значения случайной величины
сплошь заполняют некоторый промежуток
<a,b> R
(быть может,
и всю ось)
, то табличный
способ задания случайной величины
непригоден. Такая случайная величина
называется случайной величиной
непрерывного типа. Ее функция распределения
F(x) будет непрерывна. Напомним, что
F()
= 0 , F(+ )
= 1 , F(x)
монотонная неубывающая функция.
Производная такой функции F(x) будет
функцией неотрицательной. Она называется
плотностью распределения вероятностей
или дифференциальной функцией
распределения вероятностей. Ее обозначение
.
Часто по условию задачи задают именно плотность распределения, зная которую можно вычислить и (интегральную) функцию распределения ( по формуле Ньютона - Лейбница ):
F(x)
= F(x)
F(
)
=
Заметим, что f(x) не обязательно непрерывная функция, она допускает в отдельных точках разрывы 1-го рода.
Итак, f(x) неотрицательная кусочно-непрерывная функция, причем, согласно одному из свойств F(x),
F(+
)
=
=
1
Последнее
равенство, называемое условием нормировки
f(x), показывает, что f(x)
не любая неотрицательная функция:
площадь между графиком плотности
распределения и осью абсцисс должна
быть равна 1.(Для дискретной случайной
величины условием нормировки являлось
равенство
).
Для
непрерывных случайных величин справедливы
равенства F(b)
F(a)
= P(a
X
< b)
= P(a
< X
< b)
= P(a
< X
b)
= = P(a
X
b)
=
.
М(Х) и D(X) определяются формулами
M(X)
=
,
D(X) =
.
Вычислительная формула для D(X):
D(X)
= M(X2)
(M(X))2
=
(M(X))2.
§19. Нормальный закон распределения и его характеристики.
Нормальный (гауссовский) закон распределения задается плотностью распределения по формуле
,
x
Числа а R и > 0 называются параметрами нормального закона. Нормальный закон с такими параметрами обозначается N(a,).
При а = 0 функция f(x) четная ( f(x) = f(x) ) , ее график симметричен относительно оси OY, и поэтому среднее значение М(Х) = 0. График f(x) для закона N(a,) получается из графика f(x) для N(0,) сдвигом на а единиц вправо ( это известно из курса средней школы ), поэтому в общем случае М(Х) = а для нормального закона.
Дисперсия же вычисляется по формуле D(X) =2.
Пример. Случайная величина Х распределена по нормальному закону с плотностью вероятности
Найти А, М (Х), D(X), P(3<X<3).
Т.
к.
,
то
Показатель
экспоненты
приравняем к
,
откуда а = 2 ,=
1 . Числовой коэффициент
должен
быть равен А, следовательно,
,
M (X) = a = 2, D(X) = 2
= 1.
P
(3
< X < 3) = F(3)
F(3)
= =
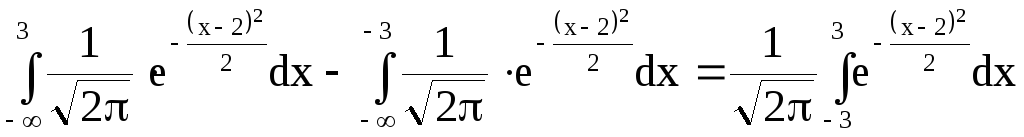
Этот интеграл не вычисляется в элементарных функциях, его численное значение можно найти по таблицам.
В большинстве учебников имеются таблицы для вычисления функций
Ф(х)
=
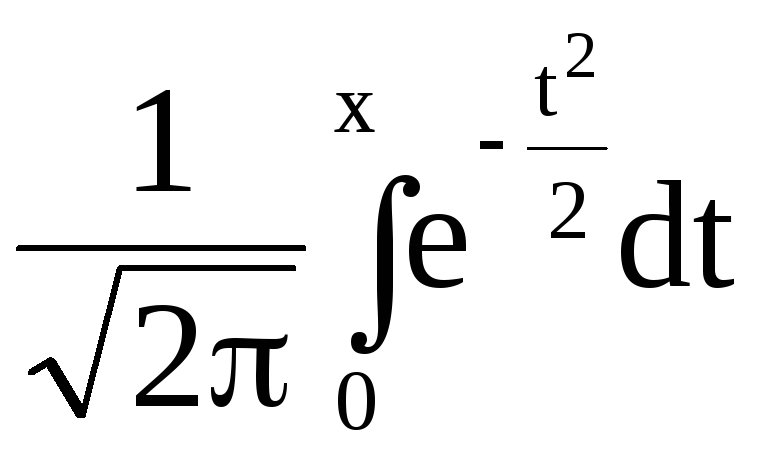или Ф1(х)
=
=
+ Ф(х)
Ф(х) нечетная функция, т.е. Ф(х) = Ф(х). В общем случае
Р(x1
< X < x2)
=
,
где а и - параметры нормального закона. Следовательно, для данного примера
P(|X| < 3) = Ф1(1) Ф1(5) = Ф(1) Ф(5) = Ф(1) + Ф(5) =
= 0,3413 + 0,5 = 0,8413.