ЧАСТЬ 1

ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ И ИХ ЭПЮРЫ

1.1. Общие положения

При нагружении твердого деформируемого тела в нем возникают силы взаимодействия между отдельными его частицами, которые называют внутренними силами. От величины и характера распределения внутренних сил зависят прочность, жесткость и устойчивость элемента конструкции, поэтому необходимо в первую очередь уметь определять эти силы.

Основным объектом всех расчетов является стержень. Под стержнем понимают тело, один размер которого значительно больше двух других.

Система внешних нагрузок и внутренних сил взаимно уравновешена, поэтому необходимо выразить внутренние силы через внешние. Для определения внутренних сил используется метод сечений. Для стержня можно применить прием мысленного рассечения его на две части плоскостью, перпендикулярной его продольной оси (рисунок 1.1, а). Затем отбрасывается одна из полученных частей и рассматривается оставшаяся. Она будет находиться в равновесии, если к ней приложить систему сил, распределенных по площади сечения. Силы, заменяющие действие отброшенной части на рассматриваемую, и есть внутренние силы в сечении.

Система внутренних сил приводится к главному вектору R и главному моменту M (рисунок 1.1, б). Главный вектор R раскладывается на три составляющие: силу N, направленную вдоль оси стержня, и силы Qx è Qy, действующие в плоскости сечения вдоль осей системы координат. Главный момент M раскладывается также на три составляющие: момент Mê, действующий в плоскости поперечного сечения относительно продольной оси z, и моменты Mx è My, действующие относительно двух взаимно перпендикулярных осей x и y, лежащих в плоскости сечения и проходящих через его центр тяжести (рисунок 1.1, в).

9

Cоставляющие главного вектора R и главного момента M называются внутренними силовыми факторами, сила N — продольной силой, силы Qx è Qy — поперечными силами, момент Mê — крутящим моментом, моменты Mx è My — изгибающими моментами.

P1

P6 P5

В общем случае в поперечном сечении возникают шесть внутренних силовых факторов, числовые значения которых определяются из шести уравнений равновесия для рассматриваемой отсеченной части стержня.

Итак, определение внутренних силовых факторов по методу сечений сводится к четырем основным операциям:

1)стержень рассекается плоскостью в некотором сечении;

2)одна из частей стержня отбрасывается;

3)действие отброшенной части заменяется внутренними силовыми факторами;

4)оставшаяся часть стержня уравновешивается, т.е. из

10

уравнений равновесия определяются значения внутренних силовых факторов в сечении.

Для наглядного представления строят эпюры — графики изменения внутренних силовых факторов по длине стержня.

В зависимости от числа действующих (не равных нулю) внутренних силовых факторов различают следующие простые виды деформации:

—центральное растяжение (сжатие): в сечении действует только продольная сила N, а все остальные внутренние силовые факторы равны нулю;

—кручение: в сечении действует только крутящий момент

Mê;

—прямой чистый изгиб: если в сечении действует только изгибающий момент Mx èëè My;

—сдвиг: в сечении действует только попречная сила Qx

èëè Qy.

При рассмотрении простых видов деформации стержней используются следующие рабочие правила определения внутренних силовых факторов.

1.Продольная сила N в сечении численно равна алгебра- ической сумме проекций всех внешних сил, действующих на отсеченную часть, на продольную ось стержня (на ось z).

2.Поперечная сила Q в сечении численно равна алгебраи- ческой сумме проекций всех внешних сил, действующих на отсеченную часть, на ось, перпендикулярную оси стержня (т.е. на ось x или y).

3.Крутящий момент Мê в сечении численно равен алгебра- ической сумме моментов всех внешних сил, действующих на отсеченную часть, относительно продольной оси стержня (оси z).

4.Изгибающий момент M в сечении стержня численно равен алгебраической сумме моментов всех внешних сил, действующих на отсеченную часть, относительно оси, проходящей через центр тяжести сечения и перпендикулярной продольной оси стержня (т.е. оси x или y).

Правила знаков для внутренних силовых факторов:

— продольная сила считается положительной, если она направлена в сторону внешней нормали к сечению и вызывает

11

растяжение отсеченной части. В противном случае она отрицательная;

—поперечная сила считается положительной, если она вызывает вращение отсеченной части стержня по часовой стрелке. В противном случае она отрицательная;

—крутящий момент считается положительным, если при взгляде на сечение со стороны внешней нормали он направлен против хода часовой стрелки. В противном случае он отрицательный;

—изгибающий момент считается положительным, если он вызывает сжатие верхних волокон в сечении горизонтального стержня. В противном случае изгибающий момент отрицательный. При построении эпюр положительный момент откладывается со стороны сжатых волокон сечения.

Общий порядок построения эпюр внутренних силовых факторов следующий.

1. Из уравнений равновесия определяют реакции опор.

Âслучае, когда имеется только одна опора в виде жесткого защемления и есть возможность все время рассматривать отсе- ченную часть со стороны свободного конца стержня, опорные реакции можно не определять.

2. Намечают на стержне силовые участки. Силовым участком считается такая часть стержня, на которой характер функций изменения внутренних силовых факторов постоянный. Границами силовых участков являются места приложения сосредоточенных сил и моментов, начало или конец распределенной нагрузки, а также места изломов оси стержня.

3. Рассматривая характерные сечения на каждом из участков, определяют значения N, Q и М. Таковыми, как правило, являются начало и конец участка при линейном изменении внутренних силовых факторов по его длине. В случае нелинейного изменения силового фактора при построении эпюры на участке

рассматривают сечение на переменном расстоянии (zi) и находят зависимость этого силового фактора от координаты z.

4. По полученным значениям строят эпюры N, Q и М. Ординаты эпюр откладывают перпендикулярно продольной оси стержня с соблюдением выбранного для каждой эпюры мас-

12

штаба. На эпюрах N и Q проставляют знаки. Значения положительных изгибающих моментов откладывают обязательно со стороны сжатых волокон, при этом знаки не ставятся. На всех эпюрах наносится штриховка обязательно перпендикулярно к продольной оси стержня.

5. Правильность построенных эпюр проверяется:

а) с помощью дифференциальных зависимостей Д. И. Журавского

б) путем проверки выполнения условий равновесия.

1.2. Растяжение (сжатие) бруса

Центральным растяжением (сжатием) называется такой вид деформации, при котором в поперечных сечениях стержня возникает только продольная сила N, а остальные внутренние силовые факторы равны нулю. Линия действия равнодействующей всех внешних сил, действующих на стержень, совпадает с его продольной осью. Следовательно, при растяжении (сжатии) строят эпюру продольной силы — ЭN.

При построении эпюры используют метод сечений. При этом необходимо иметь в виду следующие закономерности:

—в сечении, где приложена сосредоточенная внешняя сила, на эпюре продольной силы происходит скачок на вели- чину внешней силы;

—на участке стержня между сосредоточенными внешними силами продольная сила постоянная;

—на участке, где действует равномерно распределенная внешняя нагрузка, продольная сила изменяется по линейному закону.

Пример 1

Для стержня, показанного на рисунке 1.2, нагруженного сосредоточенными силами и равномерно распределенными нагруз-

13

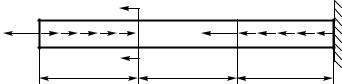
ками, построить эпюру продольной силы (в долях P). Размеры участков стержня и величины действующих сосредоточенных сил и равномерно распределенных нагрузок приведены в таблице 1.1.

Решение

1.Изображаем реальную схему задачи с учетом длин уча- стков стержня, величин и направлений действующих сил в соответствии с данными таблицы 1.1 (рисунок 1.3, а).

2.Направляем ось z вдоль оси стержня и определяем нор-

мальную реакцию в заделке RzÀ, записав уравнение равновесия стержня (рисунок 1.3, б):

Величина реакции RzÀ = –2P.

3. Эпюру продольной силы получаем методом сечений. Стержень имеет три силовых участка. Необходимо определить продольную силу в 6 сечениях, расположенных в начале и конце каждого из участков (рисунок 1.3, в).

14

15