- •4.Преобразование сигналов в нелинейных радиотехнических цепях.
- •4.1 Нелинейные элементы.
- •4.2. Способы описания характеристик нелинейных элементов
- •4.4 Бигармоноческое воздействие на нелинейный элемент
- •4.5 Влияние кубического члена вах на спектр выходного сигнала
- •4.6 Нелинейные резонансные усилители и умножители частоты
- •4.7 Получение модулированных сигналов
- •4.7.1 Принцип работы амплитудного модулятора
- •4.7.2 Получение сигнала с балансной модуляцией
- •4.8 Фазовращатели
- •4.9 Получение сигналов с угловой модуляцией
- •4.10 Функции Берга
- •4.11 Амплитудное, фазовое и частотное детектирование
- •4.12 Детектирование с использованием квадратичной аппроксимации
- •4.13 Диодный детектор ам – сигналов
4.4 Бигармоноческое воздействие на нелинейный элемент
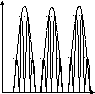
Свойство нелинейной цепи изменять спектр выходного сигнала очень ярко проявляется, если входной сигнал представляет собой сумму гармонических колебаний с разными частотами. Спектр бигармонического сигнала представлен на рис.4.5.
В системах связи бигармонический сигнал получается, когда взаимодействуют два генератора (например, генератор входного сигнала и специальный генератор с фиксированной или перестраиваемой частотой).
Пусть ВАХ нелинейного двухполюсника описывается полиномом второй степени:
![]() (4.13)
(4.13)
Тогда напряжение, приложенной к входу, помимо постоянной составляющей, содержит два гармонических колебания с различными частотами 1и2 и амплитудамиUm1 и Um2.
![]() (4.14)
(4.14)
Сигнал (4.14) называется бигармоническим. Подставив (4.14) в (4.13) будем иметь:
![]()
![]() (4.15)
(4.15)
Учитывая что
![]() ,
а
,
а
![]() получим:
получим:
![]()
![]() (4.16)
(4.16)
Спектральная диаграмма выражения (4.16) показана на рис.4.6.
4.5 Влияние кубического члена вах на спектр выходного сигнала
Если ВАХ нелинейного элемента (4.13) содержит слагаемое вида:
![]() (4.17),
(4.17),
то, подставив (4.14) в (4.13) с учетом (4.17) и проведя простейшие тригонометрические преобразования, для кубического члена получим:
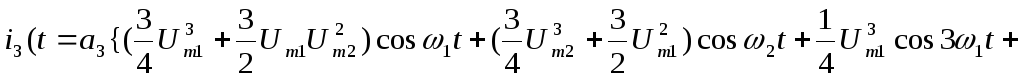
![]()
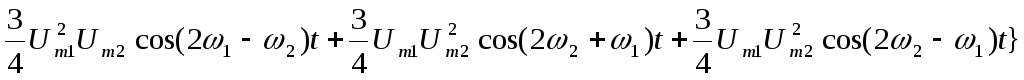
Анализ данного выражения показывает, что кубическое слагаемое несколько изменяет уровень первых гармоник сигнала, имеющих частоты и . Появляются новые спектральные составляющие с частотами3
4.6 Нелинейные резонансные усилители и умножители частоты
В технике радиопередающих
устройств широкое применение получили
резонансные усилители мощности. Их
отличительная черта – работа при больших
амплитудах входных напряжений. Рассмотрим
транзисторный усилитель с нагрузкой в
виде колебательного контура (рис.4.7). На
вход усилителя подается напряжение
вида
![]() .
.
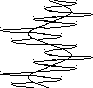
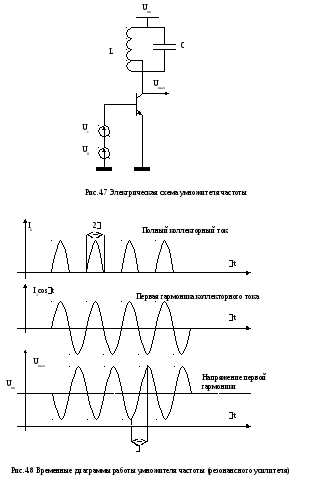
Колебательный контур настроен на частоту входного сигнала. Временные диаграммы его работы приведены на рис.4.8.
Ток в цепи коллектора имеет форму косинусоидальных импульсов с отсечкой. Эти импульсы, как это было показано ранее, обладают сложным
спектральным составом, но основную роль играет первая гармоника тока, частота которой совпадает с резонансной частотой контура.
Сопротивление контура на частотах 2 3и т.д. очень мало и таким образом высшие гармоники не дают вклад в общий сигнал.
Первая гармоника коллекторного тока создает на выходе полное напряжение с амплитудой описываемой уравнением (4.18)
![]() (4.18)
(4.18)
где
![]() - сопротивление контура на резонансной
частоте;
- сопротивление контура на резонансной
частоте;![]() - функция Берга для первой гармоники,
которая зависит от угла отсечкиколлекторного тока (функции Берга –
табулированы).
- функция Берга для первой гармоники,
которая зависит от угла отсечкиколлекторного тока (функции Берга –
табулированы).
Используя степенную аппроксимацию ВАХ биполярного транзистора (4.6) на выходе будем иметь:
![]() (4.19)
(4.19)
Если колебательный контур настроен на частоту n(n=1,2,3 …), одну из высших гармоник входного сигнала, то данное устройство может использоваться как умножитель частоты.
4.7 Получение модулированных сигналов
4.7.1 Принцип работы амплитудного модулятора
Амплитудным модулятором называется устройство, создающее на выходе сигнал вида:
![]() (4.20)
(4.20)
при подаче на входные
цепи гармонического несущего колебания
![]() и низкочастотного модулирующего сигнала
и низкочастотного модулирующего сигнала![]() .
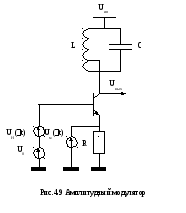
Простейшим амплитудным модулятором
служит усилитель на биполярном транзисторе
(рис.4.9).Принцип работы модулятора
поясняется диаграммой, показанной на
рис 4.10. Считается что, проходная
характеристика биполярного транзистора
аппроксимирована отрезками двух прямых.
.
Простейшим амплитудным модулятором
служит усилитель на биполярном транзисторе
(рис.4.9).Принцип работы модулятора
поясняется диаграммой, показанной на
рис 4.10. Считается что, проходная
характеристика биполярного транзистора
аппроксимирована отрезками двух прямых.
Рис.4.10 Диаграммы
поясняющие принцип работы амплитудного
модулятора
Iк
Iк t t
Uбэ t