
- •4.Преобразование сигналов в нелинейных радиотехнических цепях.
- •4.1 Нелинейные элементы.
- •4.2. Способы описания характеристик нелинейных элементов
- •4.4 Бигармоноческое воздействие на нелинейный элемент
- •4.5 Влияние кубического члена вах на спектр выходного сигнала
- •4.6 Нелинейные резонансные усилители и умножители частоты
- •4.7 Получение модулированных сигналов
- •4.7.1 Принцип работы амплитудного модулятора
- •4.7.2 Получение сигнала с балансной модуляцией
- •4.8 Фазовращатели
- •4.9 Получение сигналов с угловой модуляцией
- •4.10 Функции Берга
- •4.11 Амплитудное, фазовое и частотное детектирование
- •4.12 Детектирование с использованием квадратичной аппроксимации
- •4.13 Диодный детектор ам – сигналов
4.Преобразование сигналов в нелинейных радиотехнических цепях.
4.1 Нелинейные элементы.
Электрические цепи, содержащие линейные элементы относятся к классу линейных систем. Свойством линейных систем является принцип суперпозиции, из которого вытекает простое следствие. Гармонический сигнал, проходя через линейную систему, остается неизменным по форме. Изменяются лишь амплитуда и фаза.
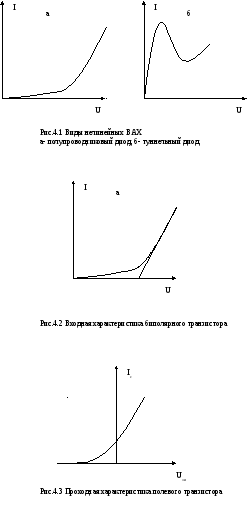
Нелинейные элементы в интегральных схемах, диоды транзисторы и т.д., имеют ВАХ нелинейного вида. Типовые примеры нелинейных ВАХ показаны на рис.4.1.
Для нелинейного элемента вводят понятие дифференциального сопротивления Rd:
![]() (4.1)
(4.1)
Иногда удобно пользоваться дифференциальной крутизной Sd:
![]() (4.2)
(4.2)
Исследование цепи с нелинейными элементами предполагает решение системы нелинейных дифференциальных уравнений, поэтому, для упрощения анализа, будем рассматривать безинерционный нелинейный элемент, т.е. элемент не обладающий реактивностями. В результате, на выходе мгновенно установится напряжение, пропорциональное входному.
4.2. Способы описания характеристик нелинейных элементов
Точную вольтамперную характеристику элементов обычно получают экспериментально. Для анализа электрических схем в ЭВМ закладывают модель элемента, ВАХ которого подчиняется некоторому закону. Данный закон в какой-то степени приближается к ВАХ реального элемента.
В радиоэлектронике чаще всего используют кусочно-линейную, степенную и показательную аппроксимацию ВАХ нелинейных элементов.
4.2.1. Кусочно-линейная аппроксимация
Кусочно-линейная аппроксимация основана на приближенной замене реальной ВАХ отрезками прямых линий с разными наклонами. Примером может служить входная характеристика биполярного транзистора
![]()
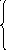
i(u)= (4.3)
![]()
Для тока коллектора вводится понятие передаточной проводимости gm:
![]() (4.4)
(4.4)
тогда для коллекторного тока будем иметь следующее выражение:
![]() (4.5)
(4.5)
где Uбэн - напряжение насыщения база-эмиттер.
4.2.2.Степенная аппроксимация
Этот способ основан на разложении нелинейной ВАХ в ряд Тейлора в окрестности рабочей точки U0
![]() (4.6)
(4.6)
где
![]()
Примером степенной
аппроксимации является
проходная характеристика полевого
транзистора,![]() ,
показанная на рис.4.3.
,
показанная на рис.4.3.
4.2.3 Показательная аппроксимация
Этот вид аппроксимации связан с представлением ВАХ нелинейных элементов с помощью экспоненциальной зависимости вида:
![]() (4.7)
(4.7)
где
I0-
ток
насыщения,
![]() при Т=300К
при Т=300К
4.3. Спектральный состав тока при гармоническом внешнем воздействии
Пусть имеется некая замкнутая электрическая цепь, содержащая источник входного сигнала, нелинейный безинерционный элемент, например диод и резистивную нагрузку.
Пусть форма входного сигнала задается гармонической функцией:
![]()
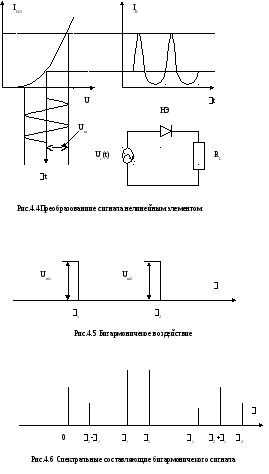
Имея ВАХ нелинейного элемента легко графически получить сигнал на нагрузке RL.Из графика на рис.4.4 видно, что форма
сигнала на выходе существенно отличается от входного сигнала, т.е. произошли его искажения. Причина искажения связана с тем, что одинаковым приращениям напряжения на нелинейном элементе отвечают разные приращения тока.
Чтобы определить состав спектральных составляющих выходного сигнала, представим зависимость выходного тока от времени следующим соотношением:
![]() (4.8)
(4.8)
где Um- максимальная амплитуда входного сигнала;U0 – напряжение в рабочей точке; =t.
Так как функция (4.8) периодическая с периодом 2, то ее можно представить в виде ряда Фурье:
![]() (4.9)
(4.9)
с коэффициентами
![]() (4.10)
(4.10)
Так как функция (4.8) четная, то разложение (4.9) будет содержать только косинусоидальные составляющие, т.е.
![]() (4.11)
(4.11)
где![]() (4.12)
(4.12)
Анализ выражений (4.11) и (4.12) показывает, что:
В спектре выходного сигнала содержится бесконечное число гармоник вида n (или n t), где n=1,2,3….
Амплитуды гармоник зависят от Um ,U0, а также от вида аппроксимации ВАХ нелинейного элемента.
