3.Случайные сигналы и шумы
3.1 Математический аппарат случайных сигналов
Раздел математики - теория вероятности, исследует случайные процессы. Отличительной чертой случайного процесса является то, что его значения (например напряжение или ток) нельзя заранее предсказать.. Поэтому, когда говорят о конкретной величине какого-нибудь случайного процесса (например напряжение на зажимах разогретого до температуры T резистора), то подразумевают его статистическую характеристику.
В теории вероятностей вводят понятия:
-функции распределения случайной величины F(x), т.е. вероятность того, что случайная величина x из множества примет значение равное или меньшее чем x0. F(x) = P(xi x0)
Для функции распределения справедливы два предельных равенства:
(3.1)
Производная от функции распределения - есть плотность вероятности:
. (3.2)
Плотность вероятности удовлетворяет условию нормировки, т.е.
(3.3)
Для случайных величин x из множества вводят понятия:
-
Математического ожидания ( m ) - среднее значение, которое может принимать случайная величина x
(3.4)
-
Дисперсии или средне - квадратичного отклонения (x2), которая характеризует меру разброса результатов испытаний относительно математического ожидания.
(3.5)
Пример 1 Равномерное распределение.
Пусть случайная величина x может принимать значения из интервала x1 x x2, причем вероятности попадания в любые внутренние интервалы равны.
Функцию распределения находят путем интегрирования плотности вероятности.
F(x)
=
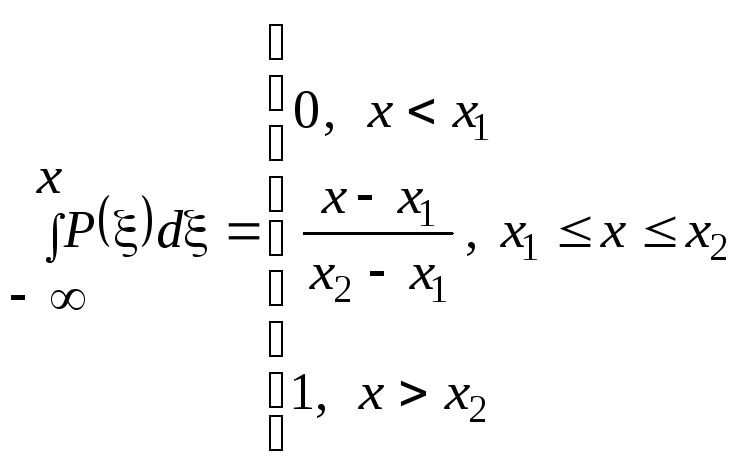
График плотности вероятности и функции распределения показан на рис.3.1.
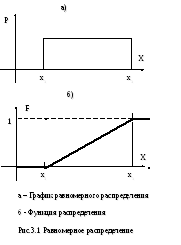
Пример 2: Гауссово (нормальное) распределение.
Плотность
вероятности гауссового распределения
(рис.3.2),
,
содержит два параметра a.
и b.
График данной функции представляет
собой колоколообразную кривую с
максимумом в точке a.
Непосредственным вычислениями можно показать, что a есть математическое ожидание, а b есть среднеквадратичное отклонение . Тогда плотность вероятности записывается в виде:
Функция распределения имеет вид:
Известный в
математике интеграл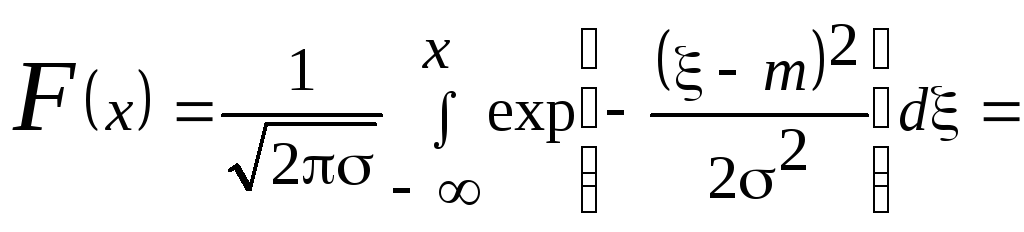
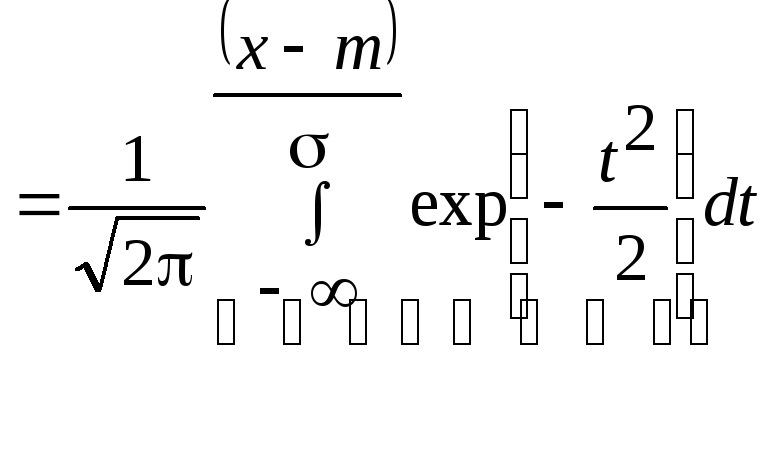
где t=(-m)
График этого распределения приведен на рис.3.2.
К случайным процессам также относятся флуктуации напряжения и тока, связанные с шумовыми явлениями в полупроводниковых приборах. Шумы определяют нижнюю границу величины электрического сигнала, который необходимо усиливать или преобразовывать с помощью полупроводниковых приборов. Поэтому необходимо знать величину и природу шумовых явлений.
3.2 Тепловой шум в резисторе ( шум Джонсона )
Причиной возникновения теплового шума является флуктуации носителей заряда в проводящих телах под действием температуры. Это могут быть резисторы или проводники в виде металлической (Al, Au, Cr, W, V) пленки, используемой в ИМС, а также пленки или объемы полупроводниковых структур. Спектр шумового напряжения теплового шума очень широк из‑за высокой плотности упаковки и высокой скорости носителей заряда.
Среднеквадратичное отклонение напряжения теплового шума резистора связано с величиной его сопротивления R выражением Джонсона -Найквиста:
, (3.6)
где R - сопротивление резистора; k = 1,38 10-23Дж/K - постоянная Больцмана, ,4kT = 1,68 10-20 Дж при T = 300 К; f - полоса пропускания, в которой измеряется шум.
Cпектральная плотность напряжения теплового шума составит:
SТ,U = 4kTR ( 3.7 )
Пример 1. При T=300 K и R=1 кОм спектральная плотность напряжения теплового шума составит SТ,U=16 10-18 [В2/Гц]. Найти чему равно шумовое напряжение.
Решение: 4 nВ/Гц1/2
Формула ( 3.6 ) имеет другой вид для среднеквадратичного отклонения тока теплового шума резистора:
(3.6а)
или для спектральной плотности шумового тока:
(3.7а)
Аналогичный расчет для R=1 кОм и T=300 К показывает, что величина шумового тока тока составит:
А/Гц1/2
Эквивалентная схема резисторов соответствующих выражениям (3.6) и (3.6а) имеют вид, показанный на рис.3.3.
Шумовые источники на эквивалентных схемах обычно заштриховывают.
