Международный тест в квадратной области. Постановка задачи

Численная схема моделирования задач космического материаловедения представляет собой сложный программный объект. В связи с этим большое значение имеет возможность проверки и тестирование численной схемы. Модельная задача в квадратной области, [11], является одной из простейших и служит общепризнанным тестом для численных схем в этой области.

Рассматривается задача 2D стационарного течения жидкости в приближении Буссинеска с числом Прандтля 0.71 в квадратной области единичной длины. На границах области обе компоненты скорости равны нулю. Горизонтальные стенки области теплоизолированы, на вертикальных стенках температура равна Т=1 и Т=0 соответственно. Задача состоит в расчете переноса тепла от горячей стенки к холодной при значениях числа Рэлея 10³, 10⁴, 10⁵ и 10⁶.

При Ra=10³ режим переноса является преимущественно теплопроводным; скорости в конвективной ячейке малы.

При Ra=10⁶ имеет место сильно развитая конвекция с большими скоростями и температурным расслоением; относительный покой жидкости в центре области и быстрое движение "пограничных слоев". В случае Ra=10⁴ и Ra=10⁵ реализуются промежуточные режимы тепломассопереноса.

Эта модельная задача хорошо отражает основные особенности задач тепломассопереноса в расплаве при росте кристаллов как в условиях микрогравитации (Ra~10³, 10⁴), так и в наземных условиях (Ra~10⁶ и выше).

При решении модельной задачи вычислялись следующие характеристики течения:

а) -функция тока в середине области

в) -максимальное в области значение функции тока;

при Ra=10³, 10⁴ =

на средней линии по х (при х=0.5)

на средней линии по z (при z=0.5).

Эти величины расположены вблизи центра области и смещаются к самой границе соответствующих пограничных слоев при увеличении числа Рэлея до Ra=10⁶

^{с) важная физическая и инженерная величина - число Нуссельта} , измеряемое на боковой стенке при х=0 (), В центре области при х=0.5 () и средняя по х величина. Можно показать, что Nu(x)=const в случае точного решения задачи.

d) локальные по z величины ипри х=0 внутри пограничного слоя. Вычисление этих величин в режиме развитой конвекции при Ra=10⁶ представляет значительные трудности и требует подробного разрешения пограничного слоя.

Тестовая задача решалась на неравномерных сетках со сравнительно небольшим числом узлов:

-31´31 и 35´35 при Ra=10³ и 10⁴,

-35´35 и 41´41 при Ra=10⁶.

Сгущение узлов сетки проводилось от центра к границам области, коэффициент геометрической прогрессии во всех вариантах был выбран Q=1.15. Расчеты проводились на двух различных сетках для каждого значения числа Рэлея, что дало возможность проследить зависимость результатов от количества узлов в пограничном слое.

Число Рейнольдса для этой задачи связано с числом Рэлея соотношением Re=(Ra/Pr)^1/2. Таким образом, числа Рэлея Ra=10³, 10⁴ и 10⁶ соответствуют числам Рейнольдса Re=37.53, 118.68 и 1186.78. При большом значении Re толщины вязкого и теплового пограничных слоев хорошо согласуются с оценочными, получаемыми по формулам . В таблицах 2 и 3 приведено примерное количество узлов в пограничных слоях для различных неравномерных сеток и чисел Рэлея Ra=10⁴, 10⁶. Там же приведено количество узлов в пограничных слоях для равномерных сеток 11´11, 21´21, 41´41 при Ra=10⁴ и 41´41, 61´61, 81´81 при Ra=10⁶, по последовательности которых в [11] экстраполяцией по Ричардсону строилось "точное" решение задачи - Bench Mark Solution (BMS).

Таблица 2.

Количество узлов в пограничных слоях для различных сеток при Ra=10⁴. Индексом 'n' отмечены неравномерные сетки.

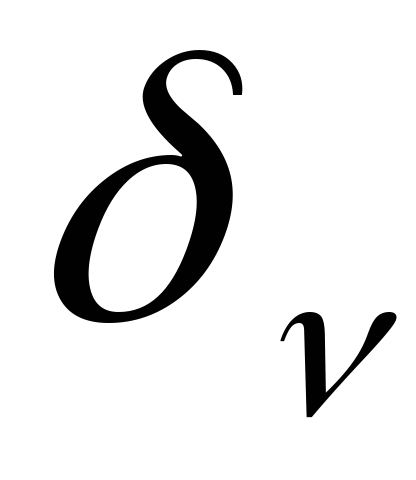	=0.092	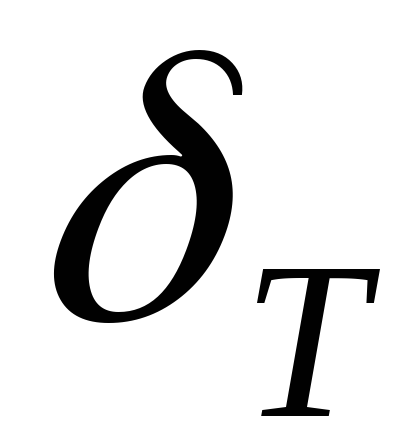=0.109
11´11	0	0
21´21	1	2
41´41	3	4
31´31n	5	6
35´35n	7	8

Таблица 3.

Количество узлов в пограничных слоях для различных сеток при Ra=10⁶.

Индексом 'n' отмечены неравномерные сетки.

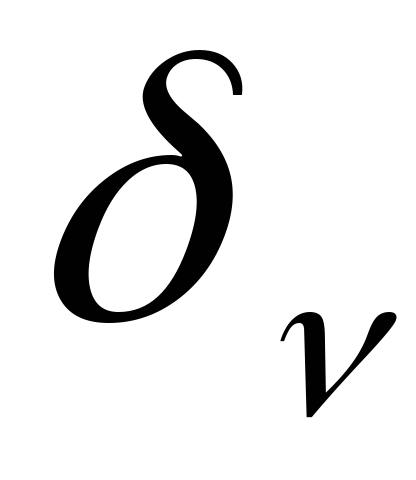	=0.029	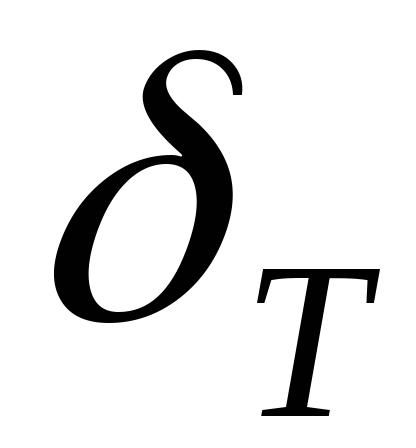=0.034
41´41	1	1
61´61	1	2
81´81	2	2
35´35n	3	3
41´41n	4	5

Несмотря на подробное разрешение пограничных слоев, общее число узлов на неравномерных сетках значительно меньше количества узлов на равномерных сетках в [11], например: 81´81/35´35»5.4. то заметно сокращает объем вычислений, стационарное решение устанавливается достаточно быстро и без подбора специальных итерационных параметров.