Дипломный проект

Спецчасть

1.1. Введение

Монокристаллы и полупроводниковые структуры широко применяются в качестве элементной базы ЭВМ, в технике связи, лазерной технике и во многих других приложениях. К однородности и структурному совершенству кристаллов предъявляются весьма высокие требования, которые непрерывно возрастают в связи с миниатюризацией всех видов электронной техники. Процессы гидромеханики и тепломассообмена, происходящие в жидкой питающей среде при кристаллизации, могут быть причиной разнообразных дефектов в кристаллах и существенно влиять на производительность и ход соответствующих технологических процессов, являясь в некотором смысле связующим звеном между условиями их протекания и структурой и свойствами получаемых кристаллов. Несмотря на то, что эти свойства в большинстве случаев хорошо изучены, физические причины, вызывающие те или иные дефекты кристаллов, исследованы в значительно меньшей степени.

Главную роль в изучении процессов роста кристаллов играет математическое моделирование этих процессов.

Разрабатываемая программа является частью системы моделирования направленной кристаллизации кристалла GaAs в условиях микрогравитации, разработанной в НИИ НЦ в отделе 261 в рамках темы " Мангут-3" между НИИ НЦ и МНТЦ Полезных Нагрузок Космических Объектов.

1.2. Постановка задачи

Программа должна реализовывать эффективный итерационный процесс, основанный на сквозной прогонке уравнения теплопроводности в криволинейных координатах. Этот итерационный процесс должен позволить одновременно вычислять смещение температурного поля на фронте кристаллизации и скорость движения фронта. Программа должна работать как часть общей Системы Моделирования Направленной Кристаллизации в условиях микрогравитации ( далее СМНК ).

Программа реализуется для двумерной модели на персональном компьютере не ниже IBM PC Pentium-100.

Программа должна быть реализована на языке программирования FORTRAN.

Должна быть предусмотрена диагностика ошибок.

2. Описание программы

1. Общие сведения.

2.1.1. Выбор языка программирования.

Исходя из того, что общая система моделирования написана на языке FORTRAN, а наша программа должна работать как часть этой системы, то для написания нашей программы будет выбран язык программирования FORTRAN.

К достоинствам этого языка можно отнести:

• язык предназначен для программирования сложных расчетных задач;

• обеспечивается высокая точность вычислений

• хорошая межплатформная переносимость

К недостаткам этого языка можно отнести слабое обеспечение структурного программирования и недостаточные возможности для эффективного процесса отладки.

В свете всего вышеперечисленного сделаем вывод, что FORTRAN в целом удовлетворяет нашим требованиям.

2. Программное обеспечение, необходимое для работы программы.

Наша программа будет работать в операционной системе MS-DOS по следующим причинам: программа реализует алгоритм, являющийся сугубо счетной задачей и требующий много времени процессора, следовательно работа в MS-DOS предпочтительнее работы в MS-Windows из-за отсутствия затрат процессорного времени на другие задачи. Ко всему прочему программа, моделирующая общую систему, тоже работает под управлением MS-DOS.

2. Функциональное предназначение.

Программа предназначена для совместного счета уравнения теплопроводности в расплаве и кристалле на центральном этапе расщепления уравнения теплопроводности, входящего в систему уравнений Навье-Стокса, описывающих физические процессы, происходящие при выращивании кристалла ( теоретические сведения об этих процессах будут рассмотрены ниже).

3. Описание логической структуры.

1. Общая постановка задачи.

В данном проекте нам предстоит построить и реализовать в виде программы часть численной схемы процессов тепломассообмена при выращивании монокристаллов.

Рассмотрим уравнения Навье-Стокса, описывающие естественную термоконвекцию расплава с малой концентрацией примеси в поле силы тяжести с постоянным ускорением . Пусть Z,и- характерный размер области, характерные плотность, температура, перепад температур и концентрации примеси в задаче, соответственно. Характерную скорость определим формулой, где- коэффициент температурного расширения расплава.

Введем безразмерные переменные

Здесь r и z - цилиндрические координаты, - вектор скорости с компонентами (u, w), t - время, p - давление, C - концентрация примеси; безразмерные переменные отмечены штрихами, которые в дальнейшем будут опущены. Числа Рейнольдса, Прандтля и Шмидта определим формулами

где v, - коэффициенты кинематической вязкости и температуропроводности расплава, D- коэффициент диффузии примеси.

Пусть рассматривается осесимметричная зона, см. рисунок; 0r0.5, 0z1.

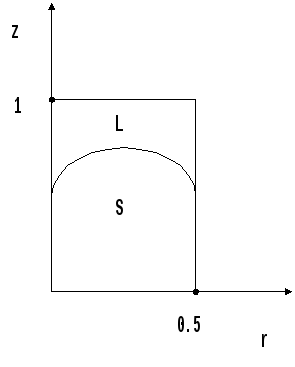
где L ( liquid ) - расплав, а S ( solid ) - кристалл.

Тогда уравнения запишутся в виде

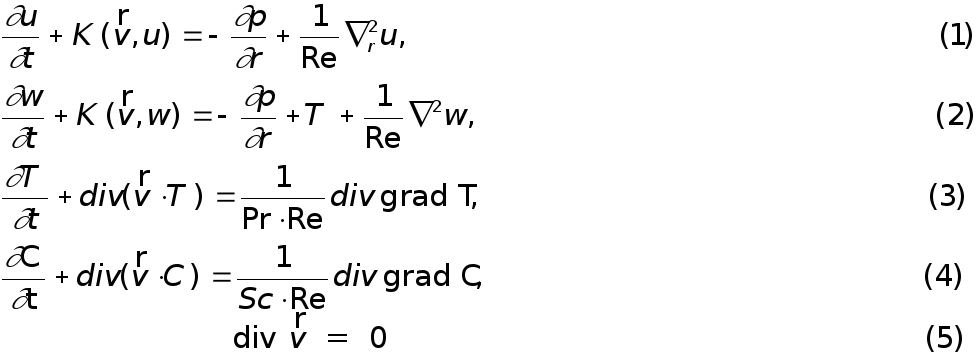
Нас будет интересовать уравнение теплопроводности (3).

Счет этого уравнения организуется методом расщепления. Сущностью этого метода является разбиение сложной физической задачи на простые подзадачи. О методе расщепления мы поговорим ниже.

2. Метод расщепления. Разбиение задачи на простые подзадачи.

Метод расщепления является одним из наиболее часто используемых методов при решении сложных дифференциальных уравнений. Этот метод заключается в разбиении основной сложной задачи на ряд простых подзадач, которые можно разрешить более простыми известными математическими методами. Эти подзадачи являются суммарной аппроксимацией исходной сложной задачи. Результаты их решения сами по себе не имеют никакого физического смысла, однако при построении расчета так, чтобы результирующие данные предыдущего уравнения были исходными данными последующего уравнения, позволяют получить решение общей сложной задачи.

Произведем разбиение нашей задачи.

Запишем дифференциальное уравнение (1)-(4) в виде

(6)

где

Через компоненты вектора обозначены все слагаемые в соответствующем уравнении, в которых отсутствуют производные по времени. Векторпредставим в удобном для нас виде

(7)

Разобьем интервал по временной координате (j, j+1) на 10 частей и определим функции в узлах с дробным индексом по времени

, n=1,...,9.

Кроме того, в точках t=t_j+(2n-1)t/20 определим промежуточные значения функций соотношением

Уравнение (6) с учетом (7) на слое (j, j+1) можно аппроксимировать со вторым порядком точности следующим образом

(8)

Схема расщепления векторного уравнения (8) имеет вид

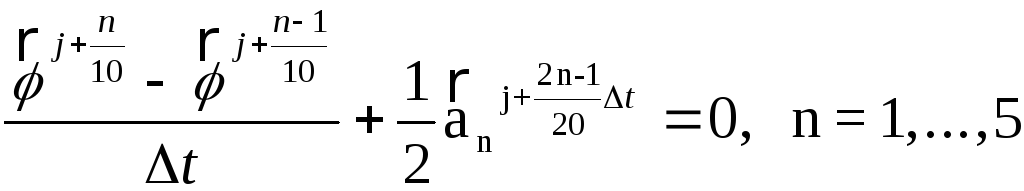(9а)

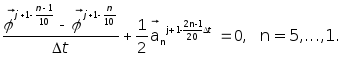(9в)

Метод расщепления состоит в последовательном (при n=1,...,5) решении уравнений (9а), затем (при n=5,...,1) решении уравнений (9в). Решения предыдущего этапа расщепления являются начальными условиями для последующего этапа. Граничные условия также подвергаются расщеплению. При сложении всех уравнений (9), а также промежуточных граничных условий получается уравнение (8) и суммарные граничные условия.

Этапы расщепления с считаются на слое по времени два раза, образуя схему симметричного расщепления, [9]. Эти этапы рассчитываются методом прогонки. Этап расщепления сявляется центральным. Это позволяет считать его на слое по времени один раз, но на интервале двойной длины.

Уравнения, полученные при расщеплении уравнения теплопроводности в более подробном виде выписаны в таблицу.

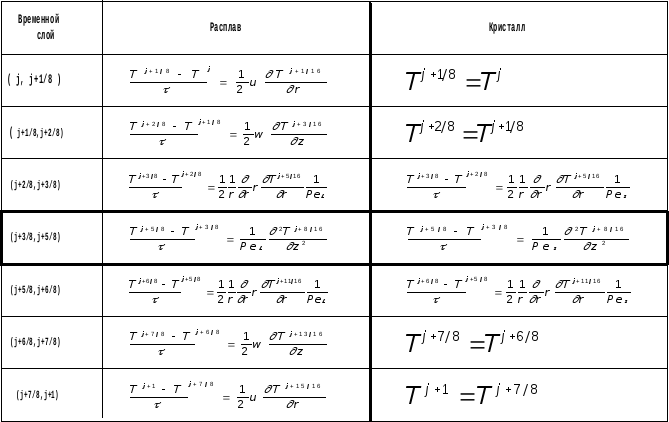
3. Организация совместного счета центрального этапа расщепления.

Организация совместного счета центрального этапа расщепления (j+3/8,j+5/8) и является основной задачей нашей программы.

Счет будет организован при помощи эффективного итерационного алгоритма, основанного на методе Ньютона, методе встречной прогонки и некоторых математических преобразований.

Рассмотрим одномерный случай.

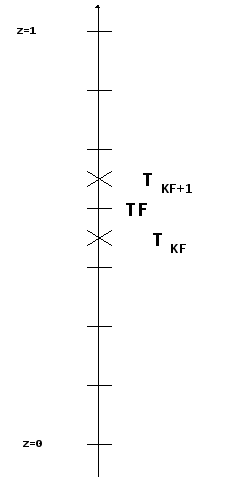
Значения функции ( температура ) определены в полуцелых узлах сетки, значение функции на фронте кристаллизации ( TF ) определено в целом узле.

Значения функции в полуцелых узлах определяются из уравнения, полученного для центрального этапа расщепления. Значение функции на фронте кристаллизации определяется из условия Стефана для фронта кристаллизации:

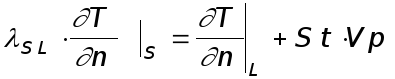
где - отношение теплопроводностей в расплаве и кристалле;

n - вектор нормали к фронту кристаллизации;

St - коэффициент обезразмеривания Стефана;

Vр - скорость роста кристалла.

У нас появляется две неизвестные величины - TF и Vp. Чтобы избавиться от одной из них, надо выразить одну неизвестную величину через другую.

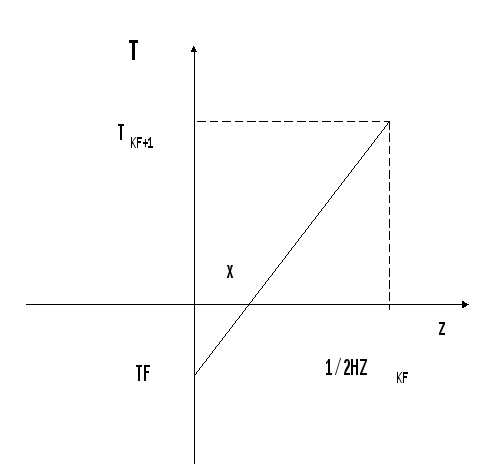
Выразим TF через Vp из следующих соображений. За шаг по времени t фронт кристаллизации сдвигается на некоторую величину. Если мы обезразмерили температуру так, чтобы на фронте кристаллизации она была равна нулю, то теперь она в этой же точке будет немного меньше нуля, а фронт сдвигается на некоторую величину x. Очевидно, что х = Vp*t. Так как шаг по времени чрезвычайно мал, то TF и x очень маленькие величины.

Из подобия треугольников имеем:

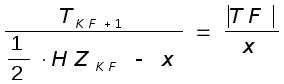
откуда

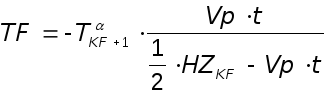
Итак, сформулирована дополнительная связь между TF и Vp.

При подстановке этого соотношения в условие Стефана на фронте кристаллизации, после математических преобразований получим:

где AS и BS - коэффициенты, а S(v)

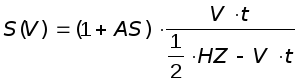
Построим итерационный процесс, основанный на методе Ньютона и методе встречной прогонки.

По методу Ньютона выразим S(V) через значение Vp на предыдущем шаге и приращение за текущий шаг.

где

V^S - значение скорости роста на предыдущем шаге;

V^S+1 - значение скорости роста на текущем шаге.

После математических преобразований, которые здесь приведены не будут, получим окончательную формулу связи скорости на предыдущем и текущем шаге итерации.

Алгоритм нашего итерационного процесса будет следующим:

на первом шаге итерации за скорость роста принимаем скорость роста на предыдущем шаге. Для быстрой сходимости метода Ньютона необходимо хорошее начальное приближение, что достигается малыми величинами t и TF. Затем при помощи алгоритма встречной прогонки рассчитывается температурное поле в расплаве и кристалле. Затем пересчитывается новое значение скорости роста из соображений, которые были описаны выше. Условием выхода из итерационного процесса служит достижение нами нужной нам точности в определении скорости роста.

Перенос итерационного процесса на двумерный случай.

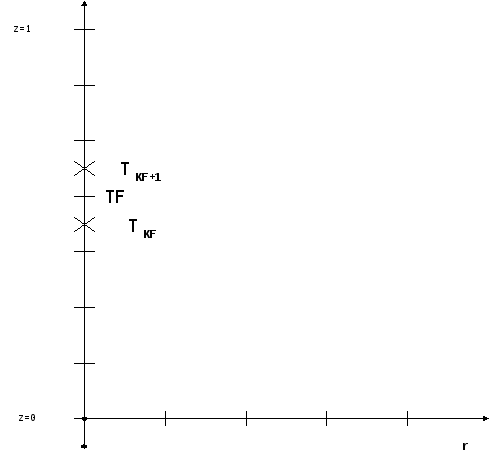
Для двумерного случая алгоритм итерационного процесса не претерпевает никаких изменений - по координате r вычисляется одномерная задача для каждого фиксированного r. Теперь становится ясно, для чего нам требовалась быстрая сходимость итерационного процесса - если бы процесс сходился медленно, то нам не хватило бы быстродействия процессора, чтобы добиться приемлемого времени расчета этой задачи.

Ниже будет подробно рассмотрен метод встречной прогонки.

4. Метод встречной прогонки.

Рассмотрим задачу

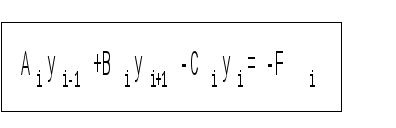
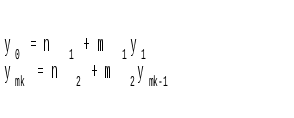
Надо указать способ решения этой системы. Идея заключается в сведении разностного уравнения второго порядка к трем разностным уравнениям первого порядка, вообще говоря, нелинейным. Предположим, что имеет место рекуррентное соотношение

y_i = Al_i+1y_i+1 + BE_i+1 с неопределенными коэффициентами Al и BE. Подставляя соотношение в исходное уравнение находятся формулы для AL и BE.

Метод встречной прогонки является комбинацией методов левой и правой прогонки. Его прогоночные коэффициенты вычисляются по формулам

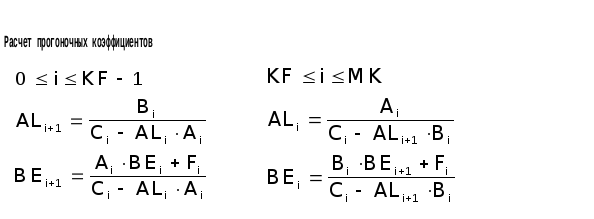
Прогонки сходятся в центральном узле i₀, который в нашем случае является фронтом кристаллизации.

Матрица встречной прогонки имеет трехдиагональный вид:

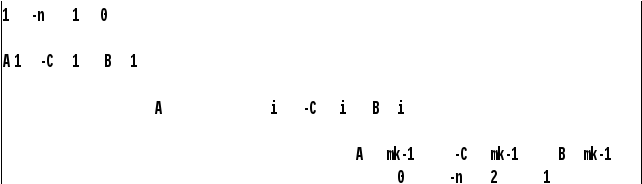
Сначала рассчитываются все A, B, C, F. Затем по рекуррентным формулам рассчитываются прогоночные коэффициенты AL и BE. В обратной последовательности рассчитываются значения функции.

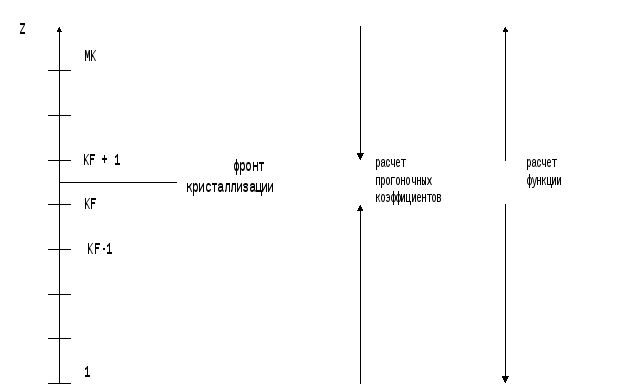
5. Структура программы. Функции ее составных частей.

1. Общая структура программы

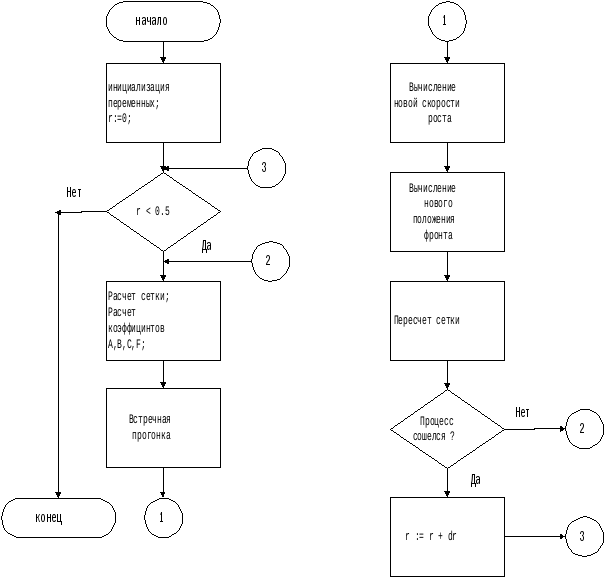
Наша программа реализует расчет перемещения фронта кристаллизации вдоль оси z и температурное поле в расплаве и кристалле за один шаг по времени. Расчет производится для двумерного случая, причем цилиндрическая координата r изменяется в пределах 0<r<0.5 ( все величины обезразмерены ). В цикле по r с шагом dr производится расчет итерационного процесса, позволяющего определить новое положение фронта ( теоретические аспекты этой проблемы были рассмотрены выше ).