3.4Метод наименьших квадратов.

В методе наименьших квадратов коэффициенты a(i) и b(i) , определяют таким образом чтобы сумма квадратов погрешностей приближения была минимальна:

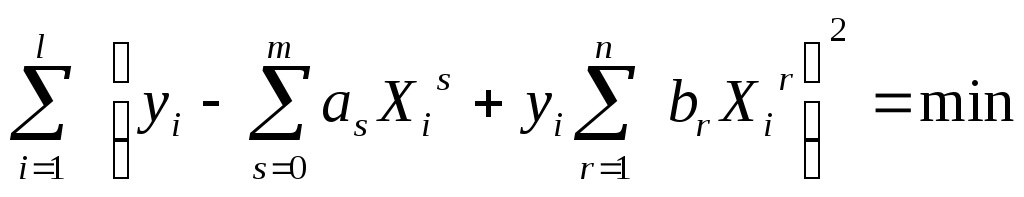(10)

где l- число точек в которых заданы значения аргумента и функции ; A b0 =1.

Дифференцируя выражение (10) по параметру aq, получают m+1 уравнений :

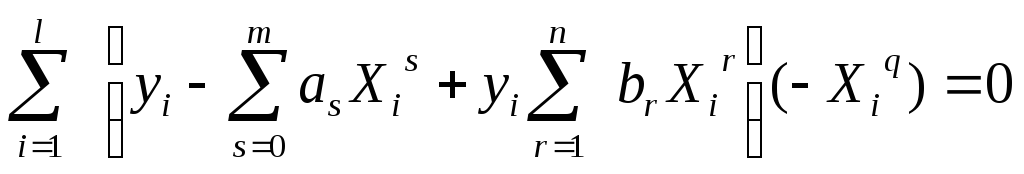(11)

где q=1,2,  m .

Дифференцируя выражение (10) по параметру br, получают n уравнений:

(12)

Решением системы уравнений (11) и (12) является m+n+1 параметр. Далее параметры уточняются с помощью весовой функции :

(13)

Выражение (10) на втором шаге принимает вид

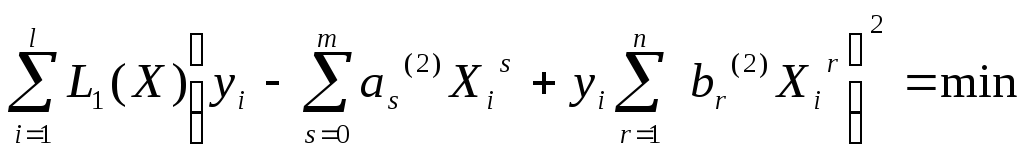(14)

где L(x) - определяется формулой (13) при значениях

параметров , найденных после первого шага.

На К-ом шаге итерационного процесса получают

(15)

Процесс вычислений считают законченным если значениясовпадают со значениямис заданной точностью.

Исследования показали , что метод итерационного веса обеспечивает нахождение минимума. При этом нулевая итерация не является минимальным среднеквадратичным приближением, но имеет более равномерное приближение.

Отметим , что методы равных площадей , степенных полиномов, интерполяции и наименьших квадратов требуют или разбиения интервала [a;b] на ряд интервалов или задания значений аргументов при которых погрешности аппроксимации равны нулю.

Современные вычислительные средства позволяют выполнять данные операции пользователю ЭВМ в диалоговом режиме , визуально контролировать характеристики получаемых приближений в виде графиков или таблиц , и производить изменения вводимых параметров с целью получения требуемых характеристик.

4. Нахождение аппроксимирующей рациональной дроби.

Аппроксимация функции

Z = F(x)y (16)

умножающей рациональной дробью

(17)

при m  n является эффективным средством моделирования зависимости (16).

При этом методическая погрешность аппроксимации в меньшей степени зависит от выбранного критерия аппроксимации и в большей степени - от числа независимых коэффициентов Ai и Bi, которые однозначно определяют количество узлов аппроксимации.

Следовательно, для достижения максимальной точности необходимо использовать рациональную дробь с максимальным количеством коэффициентов.

В этом плане заслуживает особого внимания реализация функций неумножающей рациональной дробью вида :

Z(x) = Z(0) + F1(x) (18)

где Z(0) - начальное значение функции при x=0;

(19)

Если при этом в качестве первого узла аппроксимации выбрать точку x1 = 0, то A0 всегда будет равно нулю, поэтому F1(x) можно представить в виде

F1(x) = f(x)  x (20)

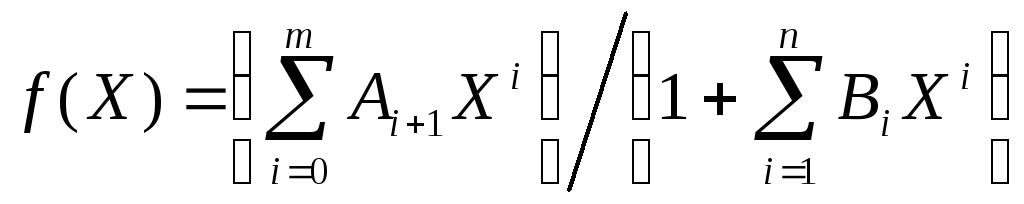где

mn (21)

Положим Z(0) = 0, тогда

Z(x) = f(x)  x (22)

Сопоставляя выражения (16) и (22) ,в связи с изложенным можно сделать следующие выводы.

Во-первых , число независимых коэффициентов в неумножающей рациональной дроби (19) на единицу больше , чем в умножающей (17) , следовательно , методическая погрешность аппроксимации должна быть почти на порядок меньше.

Во-вторых, оба преобразователя реализуются на одинаковом количестве линейных преобразователях , число которых n.

Таким образом, при сохранении оборудования можно иметь значительно меньшую методическую погрешность аппроксимации.

К разновидностям аппроксимации при помощи неумножающих рациональных дробей относятся следующие зависимости:

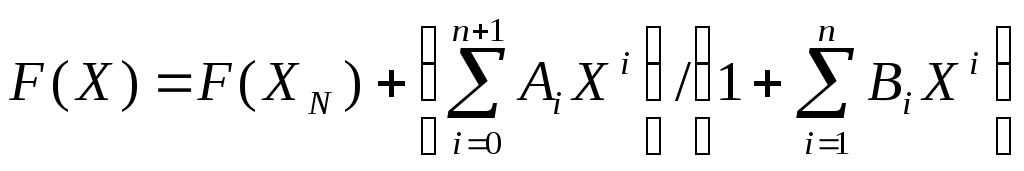
(23)

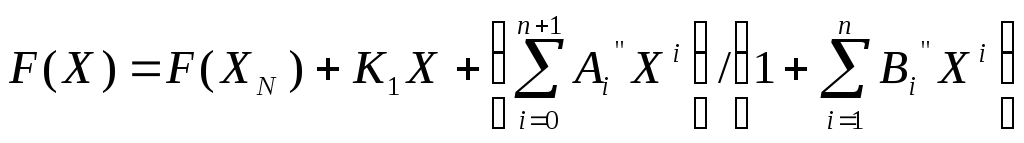
(24)

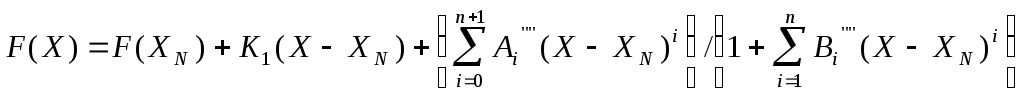
(25)

где F(XN) есть F(X) при XN ;

(26)

Из формул (23)- (26) нетрудно видеть, что коэффициенты Ai,Aiи Bi, Bi однозначно выражаются через коэффициенты Ai и Bi (23) и константы F(XN) K1 , следовательно методические погрешности для данных вариантов аппроксимации будут одинаковы.

Учитывая все вышесказанное , было принято решение использовать для аппроксимации тригонометрических функций в БТП нашего лабораторного стенда грубо-точную дробно-рациональную аппроксимацию неумножающей рациональной дробью (24).

Для расчета весовых коэффициентов и констант была использована программа аппроксимации функции неумножающими рациональными дробями APWBX2.SAV.

Программа позволяет пользователю выбрать из экранного меню тип аппроксимируемой функции, порядок n аппроксимирующей рациональной дроби и диапазон изменения X (XN , XK) , кроме того установить свое значение K1 и выбрать узлы аппроксимации в диалоговом режиме, это позволяет добиться такого распределения ошибки аппроксимации, которое будет соответствовать заданному требованию, например, наилучшего равномерного приближения.

В качестве критерия аппроксимации выбран метод интерполяции , так как первый узел аппроксимации должен быть расположен в точке x=XN . При выполнении программы на экран(печать) выводятся коэффициенты аппроксимирующей рациональной дроби Ai и Bi и результаты статической обработки которые включают в себя методическую ошибку аппроксимации в 45 точках, среднее значение ошибки аппроксимации  , максимальное значение ошибки m = Di max, дисперсию.

(27)

(28)

где i - величина отклонения текущего значения методической ошибки Di от среднего  .

В процессе многократного моделирования и анализа порядков рациональной дроби , вычисляемых коэффициентов и результатов статической обработки были получены следующие результаты :

• для аппроксимации синусной функции целесообразно использовать дробно-рациональную аппроксимацию функции SIN (/2) X , где Х  0;1 ;

• для обеспечения высокой точности (методическая погрешность максимальная м  = 0,001 ) достаточно второго порядка рациональной дроби (n=2);

Функция SIN(/2)X аппроксимируется формулой (29):

Максимальная методическая погрешность достигается при Х=0.542442 и составляет здесь 0.0011 от всей шкалы.