3.1 Интерполяционный метод.

В качестве критерия аппроксимации заданной функции f(x) рациональной дробью gn(x) принимается совпадение значений f(xk) и gn(xk) в узлах аппроксимации Xk  [a;b] , то есть

(3)

Определитель этой системы отличен от нуля , поэтому система (3) имеет единственное решение a0*,a1*, … am*; b1*… bn*.

Отсюда

(4)

где являются рациональной интерполяцией функцийf(x) на отрезке [a;b].

Отметим ,что при интерполяционном методе количество узлов аппроксимации Xk и уравнений в системе (3) совпадает и определяется числом коэффициентов a(i) и b(i) .

В общем случае неизвестно ни расположение узлов аппроксимации Xk , ни порядок рациональной дроби. Поэтому задача определения gn*(x) решается методом проб, исходя из допустимой сложности функционального преобразователя , требований по технической реализации, вероятного диапазона и допустимой погрешности.

3.2 Метод равных площадей.

Метод равных площадей может быть использован при поиске приближений в виде дроби (1) для ФП 1/1 .

Принимая b0=1 и разбивая интервал изменения аргумента [a;b] па ряд участков можно получить систему из m+n+1 линейных уравнений для однозначного определения коэффициентов a(i) и b(i):

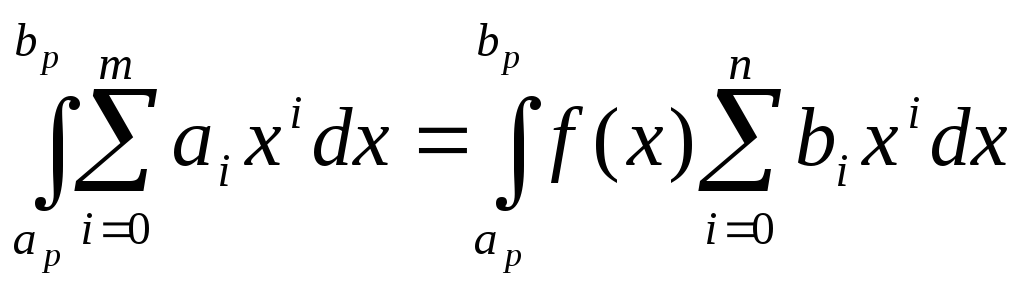(5)

где

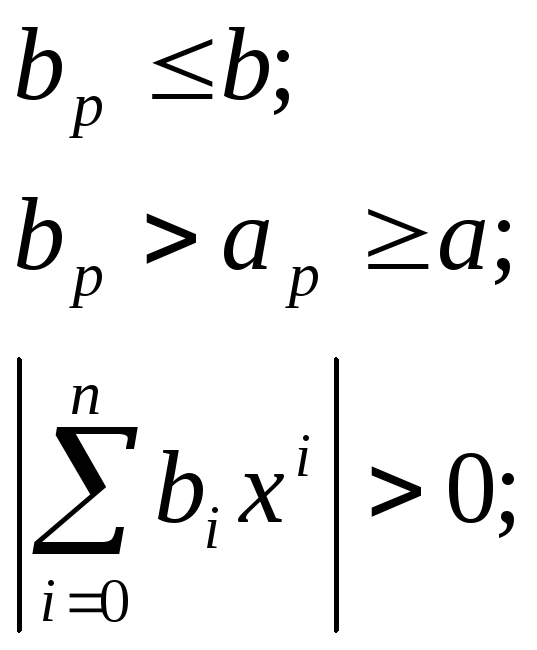
-аппроксимируемая функция.

Разбиение заданного отрезка [a;b] на поддиапазоны чаще всего равномерно. Однако если оговариваются требования повышения точности при определенных значениях аргумента, то интервалы разбиения в данном диапазоне аргумента уменьшаются.

Исследования показали , что максимальная ошибка аппроксимации имеет место на концах диапазона и быстро, в пределах x = 1 , спадает до минимума , значение которого меньше по сравнению с аппроксимацией по методу наименьших квадратов.

3.3 Метод степенных полиномов.

Если исходная функция задана степенным полиномом или известно ее разложение в ряд Тейлора ,то целесообразно использовать метод степенных полиномов ,который позволяет получить хорошее приближение функции рациональной дробью.

Достоинством метода является относительно простой алгоритм и возможность оценить предельную приведенную погрешность аппроксимации в зависимости от порядка рациональной дроби. Для функции одной переменной исходный полином имеет вид

(6)

где =m+n m=n+1 или m=n

Тогда приближение функции

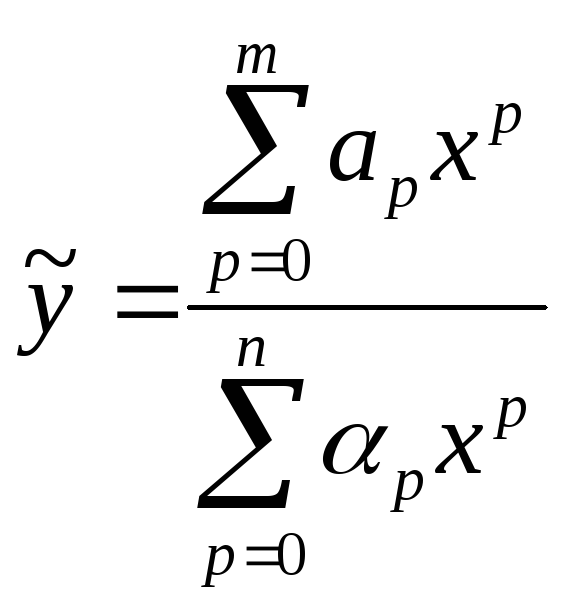
(7)

где

(8)

=p . если p < n ; =n, если p  n.

Погрешность приближенияy составит

(9)

где .

Минимизация далее осуществляется методом равных площадей. Для расчета коэффициентов p составляют систему из n линейных уравнений, для чего задается или n точек пересечения кривых (6) и (7) или область изменения аргумента разбивается на n участков, для каждого из которых площади , ограниченные кривыми (6) и (7) должны быть равны друг другу.

Недостатком метода степенных полиномов является неравномерность распределения ошибки аппроксимации , которая возрастает с увеличением аргумента.