5.2 Проверка устойчивости дрфп.

При анализе устойчивости замкнутых математических моделей рассматривают характер уравновешивания системы без учета инерционности элементов (принципиальная устойчивость безъинерционной системы) и влияние инерционности элементов на процесс уравновешивания системы (реальная устойчивости).

При исследовании реальной устойчивости , используя линеаризацию по малым отклонениям , составляют в символической форме линеаризованные уравнения динамики, принимая что усилители и множительные устройства являются инерционными звеньями. Выражают приращение искомой величины , находят характеристическое уравнение и проверяют не содержит ли оно корней с положительной вещественной частью , для чего можно воспользоваться критерий Гурвица. Для последовательного ДРФП условиями сходимости и устойчивости являются [5]:

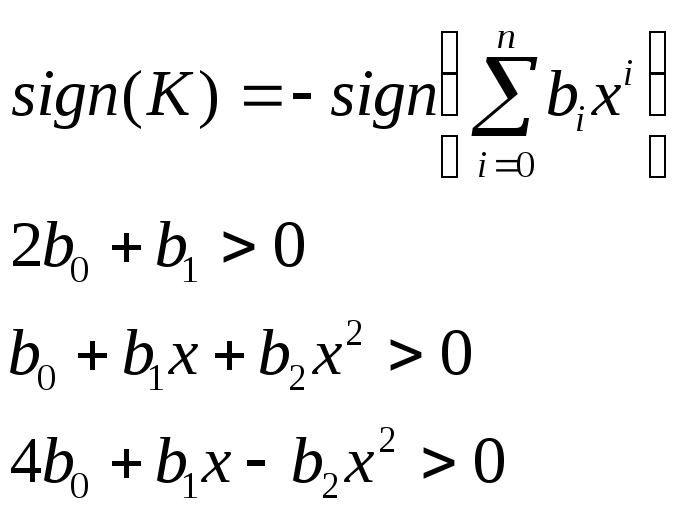
(34)

где b0,b1,b2 – коэффициенты полинома (2);

• n=2 n- порядок полинома

• sign(k) – знак коэффициента усиления усилителя , реализующего функцию сумматора обратных связей ( на рис.2- инвертирующий трехвходовый сумматор 1)

sign(k)<0.

Проверим выполнение неравенств системы (34).

Дано:

b0 = 1; b1 = - 0.071086 ; b2 = 0.166104; n =2 ; sign(k)<0 ;

тогда система запишется :

2*1-0.071086X > 0

1. 0.071086X + 0.166104X^2 >0

4*1 - 0.071086X - 0.166104X^2>2

при x[0;1]

Первое неравенство выполняется при X < 28.1,

Второе - при любых значениях;

Третье – при X[-5 ; 4.6]

(диапазоны представления Х – приближенные).

Таким образом неравенства выполняются при Х[0;1], поэтому синтезируемый ДРФП является устойчивой системой.

5.3 Разработка структурной схемы блнлсф.

БЛНЛСФ предназначен для реализации зависимостей (30), (31), (32), причем желательно чтобы преобразователь отвечал следующим требованиям:

- минимальные аппаратурные затраты;

• высокая точность;

• использование одного источника опорного напряжения;

• простота настройки;

Было синтезировано несколько схем БЛНЛСФ. В результате их оценки по вышеперечисленным параметрам выбрана структурная схема представленная на рис.3

БЛНЛСФ состоит из следующих блоков:

1. Блок управления (БУ);

2. Блок формирования сигнала (БФС);

3. Блок преобразования сигнала (БПС).

1. Блок управления

БУ состоит из набора переключателей (тумблеров -16шт.) и

кнопок Reset и “|| Загр.” .

12 тумблеров служат для ввода кода ,управляющего

напряжением на выходе БЛНЛСФ.

13-отвечает за инверсию(спад).

14-идет на БУИ (управляет инверсией для формированием

sin(cos)).

15-отвечает за формирование сигнала SIN или COS .

16-(статика/динамика),т.е переключая тумблер мы можем

посмотреть работу БТП в статике или динамике.

1.2 Блок формирования сигнала

БФС состоит из 16-ти разрядного счетчика(2 азряда не

задействованы), управляющей логики (3 элемента И-НЕ, 3

элемента исключающее ИЛИ),12 элементов

” Исключа Ющее ИЛИ “использующееся для

инверсии(спада) сигнала (к одному из входов подключается

13* разряд , а ко второму один из выходов счетчика).

1.3 Блок преобразования сигнала

БПС состоит из 12-ти разрядного ЦАПа с ОУ на выходе.

Пользователь с помощью тумблеров задает код и

необходимый режим работы(SIN или COS,

статика/динамика). Код поступает на счетные входы

счетчика , где с приходом тактовых импульсов начинается

прямой счет (т.е идет линейное нарастание).

Достигая максимального значения счетчик обнуляется ,в это

время 13-ыйразряд меняет значение с <0> на <1> и

следующий (2-ой) цикл счета поступает на ЦАП с

инверсией (т.е идет линейный спад).

По окончании 2-ого цикла ,что соответствует интервалу 0- PI/2 происходит переключение 14-ого разряда c <0> на <1>, который идет на БУИ и переводит функцию из 1-ой четверти в 4-ую.

На протяжении остального периода (pi/2—2pi) 14 разряд не меняет своего значения. По окончании 2-ого цикла 13-ый разряд меняет значение с 1 на 0 и во время 3-его цикла идет прямой счет, т.е идет линейное нарастание.

По окончании 3-ого цикла 13-ый разряд переключается с 0 на 1 и следующий (4-ый) цикл счета поступает на ЦАП с инверсией(т.е идет линейный спад). Описанная работа блока относится к случаю если тумблер находится в положении SIN (15 разряд установлен в 0 ).

На рисунке 3.1 показан случай для SIN .

Вслучае , если тумблер находится в положении COS (15 разряд установлен в 1 ):13-ый разряд устанавливается в 1. идет линейный спад .

По окончании 1-ого цикла 13-ый разряд меняет значение с <1> на <0> и следующий (2-ой) цикл счета поступает на ЦАП без инверсии (т.е идет линейное нарастание).

В начале 2-ого цикла ,что соответствует интервалу 0- PI/2 происходит переключение 14-ого разряда c <0> на <1> (в момент pi/2), который идет на БУИ и переводит функцию из 1-ой четверти в 4-ую. На протяжении периода (pi/2—3/2pi) 14 разряд не меняет своего значения. По окончании 2-ого цикла 13-ый разряд меняет значение с 0 на 1 и во время 3-его цикла идет линейный спад. По окончании 3-ого цикла 13-ый разряд переключается с 1 на 0 и следующий (4-ый) цикл счета поступает на ЦАП без инверсии (т.е идет линейное нарастание).

На рисунке 3.2 показан случай для COS .

Таким образом , в дальнейшем обработав соответствующим образом выходной сигнал с БЛНЛСФ, мы можем получить функции синуса и косинуса, а также им обратные функции, то есть арксинус и арккосинус.