
Lek_1-5_Cher
.pdfТема 1.
Общая характеристика неразрушающего контроля. Физические основы
Общая характеристика неразрушающего контроля. Физические основы Контроль методами вихревых токов Физический смысл обобщенных параметров в теории метода вихревых токов
Накладной датчик с витками круглой формы над плоским тонким листом Накладной датчик с витками прямоугольной формы
Экранный датчик с тонким листом между катушками Проходной датчик с цилиндрической тонкостенной трубой Тонкостенная труба прямоугольного профиля в проходном датчике.
Массивное изделие. Сильно выраженный скин-эффект. Индукционный датчик в переходном режиме Выводы Вопросы для самоконтроля:
Развитие современного производства в значительной мере определяется состоянием методов и средств измерения и контроля. При высоких требованиях к качеству продукции и ее надежности наиболее перспективными оказываются неразрушающие методы контроля, так как они дают возможность контролировать все 100% выпускаемых изделий или материалов.
Среди методов, позволяющих производить такой бесконтактный высокопроизводительный контроль качества продукции, важное место занимает метод вихревых токов (МВТ).
Известно, что при внесении проводящего тела в электромагнитное поле искажается первоначальная картина последнего, а в самом теле наводятся вихревые токи. Распределение вихревых токов и возмущенного поля зависит от электрофизических параметров тела, его геометрической формы и размеров, наличия разного рода дефектов (трещин, раковин и т. п.). Существо контроля качества материалов и изделий с помощью МВТ заключается в том, что при известном характере указанной выше зависимости можно, измеряя возмущенное поле или величину реакции, испытываемой источником поля, судить о свойствах исследуемого образца. МВТ широко применяется для неразрушающей дефектоскопии, бесконтактного измерения электропроводности металлов и полупроводников, измерения толщин листов, проводящих и непроводящих покрытий, диаметров прутков и труб, измерения вибраций и в ряде других областей контроля и измерений.
|
Метод вихревых токов как метод контроля качества материалов и изделий стал |
|||||||
активно развиваться в |
последние 10— 15 лет. |
За |
это |
время появилось большое |
||||
количество публикаций, |
посвященных его теории, расчету основных узлов |
|||||||
приборов |
и |
методике |
проведения |
экспериментальных |
исследований. |
Учитывая |
||
относительно |
небольшую длительность активного |
развития МВТ, можно понять, |
||||||
почему к |
настоящему |
времени еще |
не установилась |
терминология |
МВТ, а ряд |
|||
достаточно общих вопросов этого метода еще окончательно не решен. |
|
|||||||
Контроль методами вихревых токов
При контроле методами вихревых токов (МВТ) используют зависимость амплитуды, фазы, траекторий, переходных характеристик и спектра частот токов, возбуждаемых в изделии, от его формы и размеров, физико-механических свойств и сплошности материала, расстояния до датчика, частоты и скорости перемещений, в том числе вибрации.
Соответственно этому различают четыре области применения МВТ.
Рисунок 1
Области применения МВТ
Для контроля все изделие или его часть помещают в поле датчика. Вихревые токи (ВТ) возбуждают переменным магнитным потоком Ф0. Информацию о свойствах изделия датчик получает через магнитный поток Фв, созданный ВТ с плотностью δ.

Рисунок 2
Линии напряженности магнитных полей H0, Hв и плотности вихревых токов δ при контроле накладным (а) и проходным (б) датчиками
По виду зависимости сигнала датчика от времени различают четыре метода контроля ВТ: основной гармоники, высших гармоник, переходных характеристик (импульсный), многопараметровый.
Рисунок 3
Классификация методов вихревых токов
Физический смысл обобщенных параметров в теории метода вихревых токов
Задачи теории вихревых токов, как правило, математически сложны даже при простейших формах датчиков и изделий.
Всвязи с этим представляется целесообразным проанализировать физический смысл обобщенных параметров в теории метода вихревых токов на основе решения ряда задач по единой методике, выявить общие закономерности и различия.
Влитературе показано, что закономерности, выражающие зависимость вносимых сопротивлений от электроповодности контролируемого материала и частоты питающего тока, при малых и больших значениях обощенных параметров для проходного и накладного типов датчиков с витками круглой формы в первом приближении одинаковы. Однако неясен вопрос о связи обощенных параметров для двух случаев питания датчиков: синусоидальным и импульсным токами. Весьма важно знать, почему в обобщенные параметры для накладного датчика входит диаметр датчика, а в аналогичные параметры для проходного датчика – диаметр изделия.
Общие положения и определения
Рассматриваемые задачи относятся к теории электромагнитного поля. Однако строгая постановка и решение очень сильно математизируют и тем самым формализуют задачу и результаты, так что маскируется ее физический смысл.
Более привычными и понятными кажутся задачи теории цепей. Поэтому попытаемся решить ряд задач метода вихревых токов в основном в понятиях и методами теории цепей. Такая постановка задачи не нова, однако решение ее неизвестно.
Однокатушечные датчики с изделием в терминологии теории цепей можно представить схемой, показанной на фиг.1а, двухкатушечные датчики – схемой, изображенной на фиг.1б, где
 – индуктивность токовой (возбуждающей) катушки, в которой имеется ток
– индуктивность токовой (возбуждающей) катушки, в которой имеется ток  ;
;
 - индуктивность эквивалентного контура вихревых токов, активное сопротивление которого обозначено
- индуктивность эквивалентного контура вихревых токов, активное сопротивление которого обозначено  ;
;
 - взаимная индуктивность токовой катушки эквивалентного контура вихревых
- взаимная индуктивность токовой катушки эквивалентного контура вихревых
токов;
 - индуктивность измерительной катушки датчика;
- индуктивность измерительной катушки датчика;  - взаимная индуктивность контура вихревых токов и измерительной катушки
- взаимная индуктивность контура вихревых токов и измерительной катушки

Рисунок 4
Эквивалентные схемы замещения:
А. однокатушечный датчик-изделие;
Б. двухкатушечный датчик-изделеие
Под двухкатушечными датчиками следует понимать любые накладные проходные, экранные и другие датчики, имеющие отдельную ненагруженную измерительную катушку.
Все поставленные задачи решаются в системе единиц СИ. ЭДС на контуре вихревых токов  обусловлена суммой из потокосцепления
обусловлена суммой из потокосцепления  , созданного токовой
, созданного токовой
катушкой, и потока  , созданного вихревым током
, созданного вихревым током  :
:
(1)
Поскольку ЭДС на элементе  равна падению напряжения на элементе
равна падению напряжения на элементе  , можно записать:
, можно записать:
(2)
Питание датчиков синусоидальным током
В символической форме равенство (1) с учетом формулы (2) и определений коэффициентов собственной и взаимной индуктивностей можно записать в виде
(3)
где  - круговая частота изменения тока. Отсюда:
- круговая частота изменения тока. Отсюда:
(4)
ЭДС, наведенная вихревыми токами на измерительную катушку датчика:
(5)
Обычно рассматривает вносимое напряжение  .
.
Учитывая, что соотношение  есть не что иное как постоянная времени контура вихревых токов и обозначая ее
есть не что иное как постоянная времени контура вихревых токов и обозначая ее  , можно записать:
, можно записать:
(6)
Для сокращения записей в дальнейшем введем обозначение для функции, определяющей влияние параметров изделия:

(7)
Учитывая, что для однокатушечного (параметрического) датчика |
, |
получаем:
(6а)
Иногда удобнее иметь формулы, содержащие коэффициенты связи, а не взаимные индуктивности:
(8)
где  - коэффициент связи возбуждающей катушки с контуром вихревых токов;
- коэффициент связи возбуждающей катушки с контуром вихревых токов;  - коэффициент связи измерительной катушки с контуром вихревых токов. Для однокатушечного датчика
- коэффициент связи измерительной катушки с контуром вихревых токов. Для однокатушечного датчика  . Разделив оба выражения (8) на
. Разделив оба выражения (8) на
,
соответственно получим:
(9)
В общем случае все величины, входящие в последние выражения, зависят от частоты, параметров среды, взаимного расположения датчика и изделия и их геометрии.
О полученных выражениях можно сказать, что фаза вносимых напряжения и сопротивления зависит от отношения индуктивного сопротивления контура вихревых токов к его активному сопротивлению или, что то же самое, от постоянной времени этого контура, умноженной на частоту.
Более детальный расчет относительных вносимых напряжения и сопротивления выполнен для ряда конкретных случаев.
Накладной датчик с витками круглой формы над плоским тонким листом
Взаимное расположение датчика и листа показано на фиг.2. Лист понимается тонким в таком смысле, что распределение поля по его толщине можно считать равномерным. Причин для появления неравномерности распределения поля по толщине листа две: геометрическое спадание поля, определяемое средним диаметром датчика  ,
,
и спадание, обусловленное скин-эффектом, определяемое так называемой глубиной проникновения плоской волны:
(10)
где 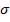 и
и  - соответственно электропроводность и магнитная проницаемость материала листа.
- соответственно электропроводность и магнитная проницаемость материала листа.

Рисунок 5
Накладной датчик над листом
Математическая запись сформулированных условий для толщины  листа имеет
листа имеет
вид
(11)
При этих условиях формула для величины активного сопротивления контура вихревых токов имеет вид
(12)
где  ,
,  и
и  - соответственно средний диаметр, ширина и длина контура вихревых
- соответственно средний диаметр, ширина и длина контура вихревых
токов.
Для величины индуктивности воспользуемся формулой из справочника:
|
|
(13) |
На основе физических соображений можно считать, что |
, как правило, лежит в |
|
пределах |
. Для этих значений функция |
. |
Теперь можно записать выражение для постоянной времени контура вихревых
токов
(14)
Этой формулой можно пользоваться, но для того, чтобы лучше просматривался физический смысл, преобразуем ее с учетом предыдущих ограничений на  . Тогда
. Тогда
получим
(15)
где  - площадь, охватываемая средним контуром вихревых токов. В другом виде:
- площадь, охватываемая средним контуром вихревых токов. В другом виде:
(16)
Поскольку формулы приближенные и смысл их заключается не в точности, причем в формулах (15) и (16) численные коэффициенты равными средним их значениям: 0,6 и 0,15 соответственно. Теперь с учетом выражения (9) можно записать
(17)
Эта формула совпадает с полученной ранее, несколько отличаясь только числовым коэффициентом.
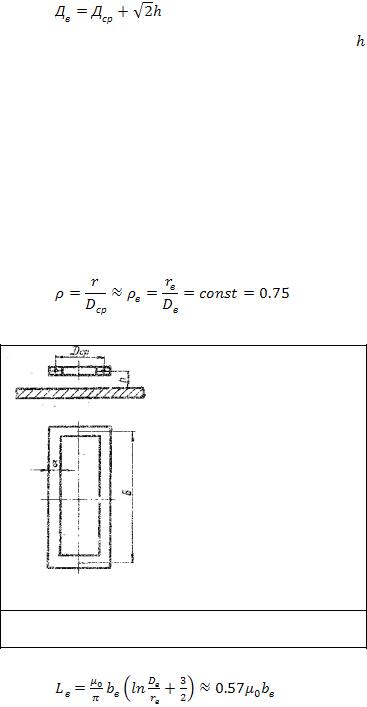
Вносимое активное сопротивление достигает максимума при равенстве активного и индуктивного сопротивлений контура вихревых токов, т.е. когда  или
или  .
.
Существенными особенностями полученных формул от известных ранее является следующее.
В качестве обобщенного параметра используется физически ясная величина – отношение индуктивного сопротивления контура вихревых токов к его активному сопротивлению.
Диаметр датчика заменен средним диаметром контура вихревых токов или отношением площади, охваченной средним контуром вихревых токов, к его длине. Последнее особенно важно. Расчеты показывают что с достаточной для практики точностью можно считать
(18)
Таким образом, с увеличением высоты |
датчика над листом увеличивается |
средний диаметр контура вихревых токов, а также обобщенный параметр  вносимого
вносимого
сопротивления. Все это приводит к тому, что годограф зазора представляет собой не прямую, а кривую с выпуклостью, направленной в сторону мнимой оси. Ясное понимание физических явлений, лежащих в основе причин, вызывающих те или иные эффекты, поможет устранить или использовать последние.
Накладной датчик с витками прямоугольной формы
Рассмотрим некоторые особенности расчета накладного датчика с витками прямоугольной формы, причем такого, у которого короткие стороны значительно меньше длинных, т.е.  (рис.6). Считаем, что ширина намотки
(рис.6). Считаем, что ширина намотки  и, следовательно,
и, следовательно, 
значительно больше толщины листа  . Будем считать, что
. Будем считать, что
Рисунок 6
Накладной датчик с витками прямоугольной формы над листом
Для расчета индуктивности контура вихревых токов подходит формула (3):
(19)
Для активного сопротивления контура вихревых токов можно записать

(20)
По аналогии с предыдущим находим:
(21)
Сравнивая последнее выражение с выражениями (15) и (16), полученными для накладного датчика с круглыми витками, видимо, что принципиальной разницы между ними нет. Вместо диаметра теперь необходимо использовать величину меньшей стороны прямоугольника вихревых токов. Даже числовые коэффициенты отличаются незначительно.
Однако следует учесть, что расчет здесь делался приближенно и только для датчика с весьма большим соотношением сторон.
Экранный датчик с тонким листом между катушками
Напряжение на измерительной катушке экранного датчика
, где |
(22) |
для тонкого диста |
|
|
(23) |
При больших значениях величиной |
(23) можно пренебречь. |
Тогда |
|
|
(24) |
Но очевидно, что  , откуда
, откуда
(25)
Теперь
, |
(26) |
(27)
Таким образом, видим, что зависимость вносимого напряжения для накладных и экранных датчиков от обобщенного параметра одна и та же при контроле тонких листов. Полное напряжение на измерительной катушке экранного датчика 
, |
(28) |
|
(29) |
Проходной датчик с цилиндрической тонкостенной трубой
Ограничимся рассмотрением однокатушечных датчиков. Взаимное положение катушки датчика и трубы приведено на фиг.4.
Диаметр трубы обозначен Д, толщина стенки Т, причем
Электропроводность материала трубы – |
, магнитная проницаемость |

Рисунок 7
Труба в проходном датчике
Для тонкостенных катушек можно пользоваться формулой (30):
(30)
Для контура вихревых токов  и
и
(31)
Активное сопротивление контура вихревых токов в данном случае
(32)
Теперь находим для проходного датчика:
(33)
Для длинного солениода:
(34)
Теперь ясно, почему с увеличением зазора за счет уменьшения диаметра образца фаза вносимого сопротивления (или напряжения) приближается к фазе тока, в то время как в случае накладного датчика при увеличении зазора вектор вносимого сопротивления поворачивается к мнимой оси.
Сравнивая формулу (34) с аналогичными для рассмотренных ранее накладных и экранных датчиков, видим, что в принципиальной части они идентичны. Несколько отличны только числовые коэффициенты.
Для погружного датчика полученные формулы справедливы.
Тонкостенная труба прямоугольного профиля в проходном датчике.
Рассмотрим случай довольно длинного соленоида. Тогда контур вихревых токов представляет собой соленоид длиной  , практически равный длине датчика
, практически равный длине датчика  .
.
Если  и
и  – соответственно короткая и длинная стороны периметра трубы, то активное сопротивление контура вихревых токов
– соответственно короткая и длинная стороны периметра трубы, то активное сопротивление контура вихревых токов
, |
(35) |
индуктивность этого контура
(36)
