
lektsii_sopromat_11-17
.pdf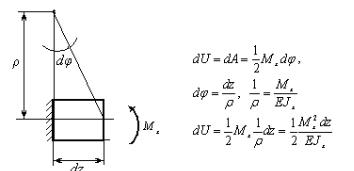
Оглавление |
|
Лекция 11............................................................................................................................................................. |
1 |
Лекция 12............................................................................................................................................................. |
9 |
Лекция 13........................................................................................................................................................... |
18 |
Лекция 14........................................................................................................................................................... |
21 |
Лекция 15........................................................................................................................................................... |
30 |
Лекция 16............................................................................................................................................................ |
39 |
|
Лекция 11. |
|
Перемещения при изгибе стержней |
|
Потенциальная энергия деформации |
При статическом нагружении упругого стержня происходит превращение работы внешних нагрузок в потенциальную энергию деформации стержня. Статическое нагружение – это нагружение, при котором нагрузка возрастает постепенно, так что ускорениями элементов конструкции можно пренебречь. При этих условиях деформация конструкции не будет сопровождаться изменением кинетической энергии системы, и будет иметь место лишь преобразование потенциальной энергии из одного вида в другой. Пренебрегая различными потерями ( электрическими, тепловыми и другими) будем считать, что вся работа внешних сил переходит в потенциальную энергию деформации балки.
При изгибе, как правило, изгибающий момент – это функция дифференцируема до второго порядка и имеющая скачки в некоторых сечениях, поэтому потенциальная энергия всей балки вычисляется как
|
|
|
|
1 l |
M x2 dz |
|
|
|
||||||
|
|
U |
|
|
|
|
|
|
. |
|
||||
|
2 |
E J |
x |
|||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|||
При поперечном изгибе потенциальная энергия определяется изгибаю- |
||||||||||||||
щим моментом M x и поперечной силой Qy |
|
|
|
|
|
|
|
|
||||||
|
1 l |
M x2 dz |
1 |
|
l |
|
Qy2 dz |
|||||||
U |
|
|
|
|
|
|
|
|
|
|
. |
|||
2 |
E J |
x |
2 |
GF |
||||||||||
|
0 |
|
|
|
|
|
0 |
|
|
|
||||
Поправочный коэффициент β зависит от формы поперечного сечения
балки

В большинстве случаев применяются балки, для которых h/L << 1, при этом 1
Оценим порядок значений потенциальных энергий от изгибающего момента и от поперечной силы на примере.
Вычислим потенциальную энергию от изгибающего момента
M x (z) P z
|
|
|
l |
|
2 |
|
|
2 |
|
j |
2 |
3 |
|
U M x |
|
1 |
|
M x |
dz |
P |
|
|
|
z 2 dz |
2P |
l |
|
2 |
|
2E bh |
3 |
/12 |
|
3 |
|||||||
|
|
0 |
EJ |
x |
|
|
0 |
Ebh |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
Вычислим потенциальную энергию от поперечной силы Qy (z) P
|
|
|
l |
2 |
|
|
|
|
|
|
|
2 |
|
j |
2 |
|
|
UQy |
|
1 |
|
Qx |
dz |
P |
|
|
dz |
P |
l |
. |
|||||
2 |
GF |
2G bh |
|
|
|||||||||||||
|
|
0 |
|
|
|
|
|
0 |
2Gbh |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Видно, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U M |
x |
|
l 2 |
|
|
|
|
|||||
|
|
|
|
|
|
U |
Q |
y |
|
h2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
То есть при l/h > 10 при поперечном изгибе потенциальной энергией от поперечной силы можно пренебречь.
Теорема Кастильано
Частная производная от потенциальной энергии системы по обобщенной силе ( силе или моменту) равна обобщенному перемещению (линейному перемещению или углу поворота) точки приложения обобщенной силы по ее направлению:
|
U |
|
|
l |
M x2 (z)dz |
|
||
u p |
|
|
|
|
|
|
|
, |
P |
P |
2 E J |
x |
|||||
|
k |
|
k 0 |
|
|
|
||
или
|
|
U |
|
|
l |
M x2 (z)dz |
|
p |
|
|
|
|
|
|
. |
M xk |
|
|
|||||
|
|
|
M xk 0 |
2 E J x |
|||
Здесь Pk , M xk - соответственно сила или момент, приложенные в точке k .

Таким образом, теорема Кастильано позволяет вычислить перемещение или угол поворота в одной точке, а именно в той точке, где приложены внешняя сила или момент.
Пример 1. Вычислить прогиб конца консоли.
.
|
1 |
l |
M x2 dz |
|
U |
|
|
|
|
2 |
E J |
x |
||
|
|
0 |
|
|
UP
|
1 |
l |
(P z)2 d z |
|
|
P2 l 3 |
||||||
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
E J |
x |
|
|
6E J |
x |
|||||
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
P2l 3 |
|
|
|
|
Pl 3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
6EJ x |
|
|
|
3E J x |
|
||
|
P |
|
|
|
|
|||||||
Вычислим прогиб балки, если сила приложена в середине балки
|
|
1 l / 2 M x2 dz |
|
|
1 l / 2 |
(P z)2 d z |
|
P2 l 3 |
|
||||||||||||
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
E J |
x |
|
2 |
|
E J |
x |
48E J |
x |
|||||||||
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|||||||||
|
U |
|
|
|
|
|
P |
2l 3 |
|
|
Pl 3 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
P |
|
|
P |
|
|
|
|
|
|
|
|
|
24E J x |
|
|
|
||||
|
|
|
|
48EJ x |
|
|
|
|
|
||||||||||||
Пример 2. Вычислить угол поворота конца консоли.
|
1 |
l |
M x2 dz |
|
|
1 l M 2 d z |
|
M 2 l |
|
|
||||||||||
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||
2 |
E J |
x |
2 |
|
E J |
x |
2E J |
|
||||||||||||
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
x |
|||||
|
U |
|
|
M 2l 3 |
|
|
|
M l |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
M |
|
M |
|
|
|
|
|
|
|
E J x |
|
|
|
|
|||||
|
|
2EJ x |
|
|
|
|
|
|
|
|||||||||||
Интеграл Максвелла-Мора
Интеграл Максвелла-Мора позволяет вычислить перемещение или угол поворота в одной, произвольно расположенной точке балки.
Выведем формулу для вычисления обобщенного перемещения ( линейного перемещения или угла поворота) в случае чистого изгиба (см. рис.).
1. В точке k, в которой необходимо определить перемещение, приложим единичную силу Pk . При этом считаем, что внешняя нагрузка отсут-
ствует. Вычислим работу Akk силы на ее собственном перемещении kk и соответствующую этой нагрузке потенциальную энергию системы U kk .
Akk |
1 |
Pk |
kk , |
U kk |
M k2 dz |
|
2 |
2EJ |
x |
||||
|
|
|
|
|
|
|
Здесь Mk - эпюра изгибающего момента во всей системе от действия силы Pk .. 2. Не снимая силы Pk , приложим внешнюю нагрузку. Вычислим работу
внешней нагрузки App и потенциальную энергию в системе U pp на ее собственных перемещениях pp .
App |
1 |
Pвн |
pp . |
U pp |
M p2 dz |
. |
|
|
|
|
|||||
2 |
2EJ |
x |
|||||
|
|
|
|
|
|
|
|
Здесь Mр- эпюра изгибающего момента во всей системе от действия все внешней нагрузки.
3. При этом сила Pk совершает работу Akp на перемещении
Akp Pk kp .
Здесь kp перемещение балки в точке k от действия всей внешней нагрузки.
4. Полная работа внешних нагрузок и силы Pk должна быть равна полной потенциальной энергии накопленной системой
|
|
|
|
|
|
|
A A A |
|
|
A |
1 |
P |
|
|
|
1 |
P P |
|
, |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
kk |
|
pp |
|
|
|
kp |
|
|
2 |
|
|
k |
|
|
kk |
|
|
2 |
|
вн |
kk |
|
kp |
|
||||||
|
|
U |
1 l |
(M p M k )2 |
dz |
|
1 l |
M p2 dz |
|
j |
M p M k dz |
|
|
1 l |
M k2 |
dz |
App Akp Akk |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
E J |
x |
|
2 |
EJ |
x |
|
|
|
|
EJ |
x |
|
|
|
|
2 |
|
|
EJ |
x |
||||||||||||||||||
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||||||
Отсюда следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
M |
p |
M |
k |
dz |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
Pk kp |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EJ x |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Представим эпюру изгибающего момента от действия усилия в виде |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M k Pk |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
k , |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1. |
||||||||||||||||||||||||||||||||||
где |
M |
k эпюра изгибающего момента от действия усилия |
Pk |
||||||||||||||||||||||||||||||||||||
|
|
Окончательно получим выражение, которое называется интегралом |
|||||||||||||||||||||||||||||||||||||
Максвелла Мора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
M |
k |
dz |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kp |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EJ x |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Итак, чтобы определить перемещение (или угол поворота) в точке k нужно знать эпюру изгибающего момента в системе от внешнего воздействия и эпюру изгибающего момента в системе от действия пробной силы (или момента), приложенной в точке k.
В самом общем виде при учете всех внутренних силовых факторов интеграл Максвелла – Мора имеет вид
|
l |
|
|
|
|
|
|
l |
|
|
|
l |
|
|
|
|
|
|
l |
|
|
|
|
|
l |
|
|
|
l |
|
|
|
|
|
|
|
M |
M |
dz |
M y M y dz |
M |
M |
dz |
N |
N |
dz |
Qy Qy dz |
Q |
Q |
dz |
|
||||||||||||||||||||
k |
|
x |
|
|
|
x |
|
+ |
|
|
|
+ |
z |
|
|
|
z |
|
+ |
z |
|
|
z |
|
+βy |
|
|
|
+ βx |
x |
|
x |
|
. |
|
EJ |
x |
|
EJ |
x |
GJ |
|
|
E F |
|
G F |
G F |
||||||||||||||||||||||||
|
0 |
|
0 |
0 |
|
0 |
|
0 |
0 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Вычисление интеграла Максвелл-Мора
1. Если эпюры имеют простой аналитический вид, то интеграл вычисляется аналитическим методом.
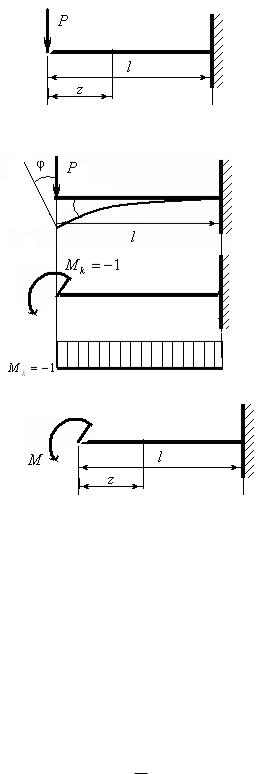
Пример 3. Вычислить перемещение и угол поворота конца консоли по интегралу МаксвеллаМора и сравнить вычисления по теореме Кастильяно.
1.1. Вычисляем вертикальное перемещение конца балки
Из рисунка видно:
M x (z) P z , |
|
|
|
||||||
|
M |
x (z) 1z . |
|
||||||
l |
|
|
|
|
|
|
|
l |
Pl 3 |
M x M x dz |
|
|
|
1 |
|||||
|
|
|
|
|
|
|
( Pz)( z) dz |
|
|
EJ |
|
EJ |
3 E J |
||||||
0 |
|
|
|
0 |
|||||
|
|
|
|
|
|
|
|
||
1.2. Вычисляем угол поворота конца балки
Из рисунка видно: M x (z) P z , |
|
|
|||||||||
|
M |
x (z) 1 . |
|||||||||
l |
|
|
|
|
|
l |
Pl 2 |
||||
M x M x dz |
|
1 |
|||||||||
|
|
|
|
|
|
( P z)( 1) dz |
|
|
|
|
|
EJ |
EJ |
2E J |
|||||||||
0 |
|
0 |
|||||||||
|
|
|
|
|
|
|
|
|
|||
1.3. Вычисляем угол поворота конца балки, нагруженной моментом
Из рисунка видно: M x (z) M ,
|
|
|
|
|
|
|
|
||
|
M |
x (z) 1 . |
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
l |
|
|
|
M x M x dz |
|
1 |
M l |
||||
|
|
|
|
|
|
|
|
( M )( 1) dz |
|
|
|
EJ |
EJ |
E J |
|||||
0 |
|
0 |
|||||||
|
|
|
|
|
|
||||
2. Если эпюры имеют сложный характер, то вычисление интеграла производится приближенным методам. Здесь используется приближенная формула Симпсона
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M x M x dz |
|
l |
|
|
|
|
|
|
|
|
|
|
||||
|
|
M x |
(0) M x |
(0) |
4M x (l / 2) M x (l / 2) M x (l) M x (l) |
|||||||||||
EJ |
6E J |
|||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Формула Симпсона применима при выполнении условий:
1.Ось балки должна быть прямолинейной.
2.Жесткость балки EJx на рассматриваемой длине должна быть постоян-
ной.
3. Грузовая эпюра Мр должна быть монотонно изменяющейся функцией. 4. Эпюра M x должна быть линейной функцией.
Если эти условия не выполняются на всей длине балки, то ее длина разбивается на несколько участков, в пределах которых указанные ограничения выполняются.
Пример 4 Вычислить вертикальное перемещение в середине балки и угол поворота балки в левой опоре.

Значения эпюр в точках z=l/4, z=l/4 равны:
M x (l / 4) |
3 |
ql 2 |
, M x (l / 2) |
1 |
ql 2 |
|||||
32 |
8 |
|||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
k (l / 2) l / 4 , |
|||||||
|
M |
k (l / 4) l / 8 , |
|
M |
||||||
M (l / 2) 1/ 2
Вычислим перемещение в центре балки
k
k
|
l |
M x M x dz |
|
|
2 l |
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
l |
|
l |
|
|
|
l |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M x (0) M x |
(0) 4M x ( ) M x ( |
|
) M x ( |
|
) M x ( |
) |
|||||||||||||||||||||
|
|
|
|
|
|
6E J |
|
|
|
||||||||||||||||||||||||||
|
0 |
|
EJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
4 |
|
2 |
|
|
|
2 |
|
||||||
2 |
l |
(0 4 |
|
3 |
ql 2 |
|
1 |
|
1 |
ql 2 |
|
l |
) |
5 ql 4 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
6 E J |
|
|
32 |
|
|
|
8 |
|
8 |
|
|
|
4 |
|
384 E J |
|
|
|
|
|
|
|
|
|
||||||||
Вычислим угол поворота левого конца балки
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
M x |
M dz |
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
M x (0) M (0) 4M x (l / 2) M (l / 2) M x (l) M (l) |
||||||||||||||||||||
|
EJ |
|
6E J |
|||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
l |
(0 1 4 |
1 |
ql 2 |
|
1 |
0) |
ql 2 |
. |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
6 E J |
|
|
|
|
8 |
|
|
2 |
|
|
24 E J |
||||||||
Метод начальных параметров
Этот метод, в отличии рассмотренных выше, позволяет определить функцию прогиба на всей длине балки.
Выше было показано, что мерой деформации при прямом чистом изгибе является кривизна нейтрального слоя
1 |
|
M x |
. |
(11.1) |
|
|
|||
|
E J x |
|
||
Кривизна не всегда удобный параметр при расчетах балок на изгиб. Удобнее пользоваться вертикальным смещением (прогибом) v и углом поворота υ сечений балки. Угол поворота связан с прогибом приблизительным выражением
dd vz .
При предположении, что h/l = << 1, приведенным выражением для кривизны можно пользоваться и в случае прямого поперечного изгиба.
Из дифференциальной геометрии известно выражение кривизны в прямоугольных декартовых координатах
1 |
|
|
|
1 |
|
|
|
|
|
d 2 v |
. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
3 |
|
|
dz 2 |
|
|
|
dv |
2 2 |
||||||||
|
|
|
|
|
|
||||||
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||||||
|
|
|
dz |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||

|
|
|
|
|
d v |
2 |
|
|
|
|||||
Если v |
max |
/ l 1 , то величиной |
|
|
|
|
|
|
можно пренебречь, поэтому вы- |
|||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
d z |
|
|
|
|
|||||
ражение для кривизны упрощается |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
|
d 2 v |
. |
(11.2) |
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
d z 2 |
|
|||||||
Подставив выражение (11.2) в (11.1), получим дифференциальное уравне- |
||||||||||||||
ние прямого изгиба балки |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
d 2 v |
|
M x |
. |
|
|||||||
|
|
|
d z 2 |
|
|
|||||||||
|
|
|
|
|
|
EJ x |
|
|||||||
Считаем, что EJ x const в пределах рассматриваемого участка.
Сущность метода начальных параметров состоит в том, что для каждой нагрузи (сосредоточенных изгибающих моментов, сосредоточенных усилий, равномерно распределенной нагрузки) общий интеграл дифференциального уравнения упругой линии (*) строится как набор частных решений, соответствующих каждой из упомянутых нагрузок. При этом в качестве произвольных постоянных выбираются прогиб v(0) v0 , угол поворота (0) 0 , изгибающий
момент M (0) M 0 , поперечная сила Qy (0) Q0 в начале координат.
Если выражение для прогиба v(z) известно, то внутренние силовые факторы ( изгибающий момент и поперечная сила) равны
|
|
M |
|
(z) EJ |
|
|
d 2 v |
, |
Q |
|
(z) |
dM x |
|
EJ |
|
|
d 3v |
, |
q |
|
dQx |
EJ |
|
|
d 4 v |
. |
|||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
x |
|
|
dz 2 |
|
|
y |
|
|
|
dz |
|
|
|
|
|
x |
|
|
dz3 |
|
|
|
|
dz |
|
|
|
x |
|
|
dz 4 |
|||||||||
Эти выражения справедливы и при z = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
M |
|
(0) M |
|
|
EJ |
|
|
d 2 v |
| |
|
, Q |
|
|
(0) |
Q |
EJ |
|
|
d 3v |
| |
|
, q q |
|
EJ |
|
|
d 4 v |
| |
|
|
|
||||||||||||||||||
|
x |
|
0 |
|
|
x |
|
dz 2 |
|
0 |
|
|
y |
|
|
|
0 |
|
|
|
x |
|
dz3 |
|
|
|
0 |
|
|
|
|
0 |
|
|
x |
|
dz 4 |
|
0 |
|
|||||||||
Функцию прогиба представим в виде ряда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
v(z) a |
0 |
a z a |
z 2 a |
z3 a |
z 4 |
.. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Константы определим из значений функции прогиба и ее производных в |
|||||||||||||||||||||||||||||||||||||||||||||||||
начале участка (при z = 0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Вычислим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dv(z) |
a 2a |
z 3a |
z 2 |
4a |
z 3 .. ., |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz |
|
|
|
|
|
1 |
|
2 |
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
полагая z = 0, получим dvdz |0 a1 .
Последовательно дифференцируя выражение для прогиба, определим значения всех последующих констант
a2 |
1 |
|
d 2 v |
|0 |
, a3 |
1 |
|
1 |
|
d 3v |
|
|0 |
1 |
|
d 3v |
|
, и так далее |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2 dz 2 |
|
|
|
|
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
2 |
|
3 dz 3 |
|
|
dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Таким образом, выражение для прогиба будет иметь вид |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dv |
z d 2 v |
|
|
|
z 2 |
|
d 3 z |
|
|
z3 |
|
|
|
d 4 v |
|
z 4 |
|||||||||||||||||
|
|
|
|
|
v(z) v(O) |
|
|0 |
|
|
|
|
|0 |
|
|
|
|
|
|
|0 |
|
|
|
|0 |
|
|
... . |
||||||||||||||||||
|
|
|
|
|
dz |
1! |
dz 2 |
2! |
dz3 |
3! |
dz 4 |
4! |
||||||||||||||||||||||||||||||||
Используя выражения (*), получим окончательно |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
M |
0 |
|
|
z 2 |
Q |
|
z3 |
|
|
q |
0 |
|
z 4 |
|
|
|
||||||||||
|
|
|
|
|
v(z) v0 0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
... |
|||||||||||||||||
|
|
|
|
|
|
|
|
EJ x |
|
|
|
|
|
|
|
EJ x |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1! |
|
|
|
|
|
2! |
|
|
EJ x |
3! |
|
|
4! |
|
|
|
||||||||||||||
Это выражение справедливо, если на рассматриваемом участке все функции непрерывны. Если это не так, то вся длина разбивается на несколько интервалов, на каждом из которых выполняются условия непрерывности. При

этом в начале каждого k – го интервала учитываются возможные скачки перемещений v(a j ) , углов наклона (a j ) , изгибающих моментов M (a j ) , попе-
речных сил Q(a j ) и интенсивности распределенной нагрузки скачки могут входить и опорные реакции (усилия и моменты).
q(a j ) . В эти
|
|
|
z |
|
|
M |
|
|
z |
2 |
|
|
|
|
Q0 |
|
z |
3 |
|
|
|
q0 |
|
z |
4 |
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|||
vk (z) v0 |
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
v(a j ) |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
EJ x |
|
|
|
EJ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
1! |
|
2! |
|
|
|
3! |
|
|
EJ x |
4! |
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
k 1 |
(z a |
|
) |
|
|
k 1 |
M |
(a |
|
) |
|
(z a |
|
)2 |
|
k 1 |
Q |
|
|
(z a |
|
)3 |
k 1 |
q(a |
|
) |
|
(z a |
|
)4 |
|
|||||||||||
(a j ) |
|
j |
|
|
|
|
|
x |
|
|
j |
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
y |
|
|
j |
|
|
|
j |
|
|
|
j |
|
... |
|||
1! |
|
|
|
EJ x |
|
|
|
|
2! |
|
|
|
EJ x |
3! |
|
|
EJ x |
|
|
4! |
|
|
||||||||||||||||||||
j 1 |
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
j 1 |
|
|
|
j 1 |
|
|
|
|
|
|
||||||||||||||||||
Если часть начальных параметров неизвестна, то они определяются из граничных условий.
Пример 5. Построить эпюры прогиба балки, углов наклона, изгибающих моментов, поперечной силы.
Из уравнений статики определим опорные реакции: A Q0 |
qa , |
B 5qa . |
На рисунке показаны начальные параметры на левом конце балки и скачки внутренних силовых факторов в начале всех последующих интервалов
Составим выражение для прогиба балки на всех участках.
v(z) v0 |
0 |
z |
M z 2 |
|
Q z3 |
|
M (z a / 2)2 |
| |
2 ( |
P (z a)3 |
|
q (z a)4 |
B (z 2a)3 |
||
0 |
0 |
|
|
|
) |3 |
|4 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2EJ |
|
6EJ |
|
2EJ |
|
|
6EJ |
|
24 EJ |
6EJ |
||

Значение начального угла наклона 0 |
неизвестно. Для его определения восполь- |
|||||||||||||||||||||||||||||||||||||||
зуемся граничным условием на правой опоре: v(2a) 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
v(2a) 0 |
2a |
|
Q (2a)3 |
|
M (2a a / 2)2 |
|
2 ( |
P (2a a)3 |
|
q (2a a) |
4 |
) |3 0 . |
|
|||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
6EJ |
|
|
|
|
2EJ |
|
|
|
|
|
|
|
|
6EJ |
|
|
|
|
|
24 EJ |
|
|
|
|
|
|
|||||||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1.396 |
qa 4 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Определим последовательно выражения для углов наклона, изгибающего |
|
|||||||||||||||||||||||||||||||||||||||
момента, поперечной силы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
Q z 2 |
|
|
M (z a / 2) |
|
|
|
|
P (z a)2 |
q (z a)3 |
|
B (z 2a)2 |
|
||||||||||||||||||||||||
(z) (((( 0 |
|
|
0 |
|
|
) |1 |
|
|
|
|
|
|
|
) |2 |
( |
|
|
|
|
|
|
|
|
|
|
|
|
)) |3 |
|
|
|
|
) | |
|
||||||
|
|
|
|
|
|
|
EJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|||||||||||||||
|
|
|
|
2EJ |
|
|
|
|
|
|
|
|
|
|
|
3EJ |
6 EJ |
|
|
|
3EJ |
|
||||||||||||||||||
|
|
(z) EJ |
|
d 2 v |
Q z M | |
|
(P |
(z a) |
q (z a)2 |
|
|
B (z 2a) | |
|
|
|
|||||||||||||||||||||||||
M |
x |
|
|
|
|
2 |
|
|
|
) | |
3 |
4 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
dz 2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Qy (z) EJ d 3v Q0 (P q (z a)) |3 B |4 dz3
По этим выражения построены эпюры
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.67 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V(z) |
0.67 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0.33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(z) |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
|
0.33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0.67 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.67 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0.25 |
0.5 |
0.75 |
1 |
1.25 |
1.5 |
1.75 |
2 |
2.25 |
2.5 |
2.75 |
3 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
Вопросы к лекции.
1.Потенциальная энергия при изгибе стержней.
2.Вычисление перемещений. Формула Кастилиано.
3.Вычисление перемещений. Формула Максвелла-Мора.
4.Вычисление интеграла Максвелл-Мора.
5.Вычисление перемещений методом начальных параметров.
Лекция 12.
Статически неопределимые задачи при изгибе стержней
Стержневая система называется статически определимой, если все внутренние силовые факторы можно найти из независимых уравнений статики. В противном случае система называется статически неопределимой. Степенью статической неопределѐнности называется разность n между числом неизвестных внутренних силовых факторов, опорных реакций и числом независимых уравнений статики.
Статически неопределимые системы имеют лишние связи. Число лишних связей называется степенью статической неопределимости.

Способы определения степени статической неопределенности
1. Отбрасывание лишних связей. Применяется для простых систем. Степень статической неопределимости равна числу связей, которые необходимо отбросить, чтобы получить статически определимую систему.
На рисунке приведѐна статически неопределимая балка, у которой число внешних неизвестных реакций в опорах равно пяти, а независимых уравнений равновесия можно составить только три. Отбрасывая две опоры и заменяя их неизвестными усилиями Х1, Х2, получим статически определимую систему.
2. Метод замкнутых контуров. Замкнутый плоский контур имеет три лишние связи
Простой шарнир в замкнутом контуре обращает изгибающий момент в этом сечении в нуль, то есть позволяет составить дополнительное уравнение, снижая, таким образом, на единицу степень статической неопределимости. Если в шарнире сходятся m шарниров, то можно составить kш = (m-1) условий.
Степень статической неопределимости определяется по формуле
n3 C kш(i) .
i 1N
где C - количество замкнутых контуров, N - число узлов с шарнирами, kш(i ) - кратность i - го шарнира.
При подсчете числа контуров и шарниров необходимо учитывать опорные стержни и присоединяющие их шарниры, и опорную поверхность.
Пример 1. Определить степень статической неопределимости
