
lektsii_sopromat_1-5
.pdfФедеральное государственное бюджетное образовательное учреждение высшего профессионального образования
Национальный исследовательский университет «МЭИ»
ЭЛЕКТРОННЫЙ УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС
ЛЕКЦИИ
дисциплины базовой части профессионального цикла Б.3.12
«Прикладная механика»
Направление подготовки 140400 Электроэнергетика и электротехника….
Профиль Динамика и прочность машин, приборов и аппаратуры
Автор:
Доцент кафедры ДПМ _________________ Ю.П. Самсонов
Москва |
2012 |
НИУ «МЭИ» |
|
Оглавление |
Лекция 1 |
...............................................................................................................................................................1 |
Лекция 2............................................................................................................................................................... |
7 |
Лекция 3............................................................................................................................................................. |
16 |
Лекция 4............................................................................................................................................................. |
26 |
Лекция 5............................................................................................................................................................. |
34 |
Лекция 1
Модели прочностной надежности. Статические уравнения равновесия
Литература
1.Феодосьев И.И. Сопротивление материалов. М.: Наука, 1999. 592 с.
2.Феодосьев В.И. Избранные задачи и вопросы по сопротивления материалов.М.: Наука-Физматлит, 1998. 375 с.
3.Биргер И.А., Мавлютов Р.Р. Сопротивление материалов. М.: Наука, 1986.560 с.
4.Окопный Ю.А., Радин В.П., Чирков В.П. Механика материалов и констркций М.: Мишиностроение, 2002. 436 с.
5.Писаренко Г.С., Яковлев А.П., Матвеев В.В. Справочник по сопротивлению материалов. Киев: Наукова думка, 1988. 725 с.
6.ИцковичГ.М., Минин Л.С., Винокуров А.И. Руководство к решению задач по сопротивлению материалов. М.: Высшая школа, 1999. 590 с.
7.Окопный Ю.А., Радин В.П., Хроматов В.Е., Чирков В.П. Механика материалов и констркций. Сборник задач. М.: Мишиностроение, 2004. 413 с.
7.Алмаметов Ф.З., Арсеньев С.И., Курицын Н.А., Мишин А.М. Расчетные
икурсовые работы по сопротивлению материалов. М.: Высшая школа,
2003. 360 с.
8. Справочник по проектированию линий электропередач. Под ред. М.А. Реут, С.С. Рокотян. М. Энергия, 1980, 296 с.
Основные понятия
Сопротивление материалов – наука о прочности, жесткости и надежности элементов инженерных конструкций. Основные понятия сопротивления материалов опираются на законы и теоремы общей механики и в первую очередь на законы статики.
В отличие от теоретической механики сопротивление материалов рассматривает задачи, где наиболее существенными являются свойства деформируемых тел, а законы движения тела, как жесткого целого, не только отступают на второй план, но в ряде случаев являются попросту несущественными.
Расчет конструкции состоит в правильном описании самой конструкции, в правильном учете внешних воздействий, в назначении таких геометрических размеров конструкции, чтобы обеспечивалась ее работоспособность.
Введем основные понятия, принимаемые при изучении дисциплины.

Надежность – это свойство конструкции (или модели) выполнять заданные функции, сохраняя свои эксплуатационные показатели в определенных пределах в течение заданного промежутка времени (наработки). Как правило, надежность связывается с определенным сроком службы. Под сроком службы понимается время работы конструкции под нагрузкой или число циклов нагружения. Допустимый срок службы изделия называется ресурсом. В ряде случаев в связи с коррозией и старением материала изделия ресурс может ограничиваться календарным временем хранения или эксплуатации.
Прочностная надежность – это отсутствие отказов, связанных с разрушением или недопустимыми деформациями элементов конструкции. Отказ – это нарушение работоспособности. Прочностная надежность включает в себя: прочность, жесткость и устойчивость.
Прочность – это способность конструкции не разрушаться под действием заданных нагрузок.
Жесткость – способность конструкции сохранять форму и размеры под действие нагрузок.
Устойчивость – это способность конструкции сохранять первоначальное состояние равновесия или заданный режим работы.
Деформирование – свойство конструкции изменять свои геометрические размеры и форму под действием внешних сил.
Модели прочностной надежности
Моделью называется совокупность представлений, зависимостей, условий, ограничений, описывающих процесс работы конструкции.
Модель – это отражение объективной реальности. Модели имеют разную природу, структуру, язык и форму представления. Наиболее часто используются математические модели, которые отображают реальность м помощью установления зависимостей между параметрами конструкции в виде уравнений (алгебраических, интегральных, дифференциальных и так далее).
Для определения критериев прочностной надежности вводят модели материала, формы, нагружения и разрушения.
На рис.1.1 приведена структура модели прочностной надежности.
Рис.1.1. Структура модели прочностной надежности элементов конструкций
Модели материалов.

В качестве материалов машиностроительных конструкций используются в основном металлы и сплавы, а так же пластмассы, керамика, разнообразные конструкционные материалы.
1.Физическая модель. Для описания поведения материалов под действием нагрузок рассматривается модель материала в виде кристаллической решетки атомов. Такие модели используются для изучения влияния несовершенств кристаллической решетки на прочность, но они не дают оценки механических свойств реальных материалов.
2.Инженерно-физическая модель – это представление материала как совокупность зерен с различной ориентированной кристаллической структурой. Такие модели позволяют объяснить ряд особенностей поведения материала в малом объеме, но не могут служить для оценки прочности всего материала.
3.Инженерные модели – это модели сплошной среды, наделенной свойствами сплошности, однородности и изотропности. Свойство сплошности позволяет рассматривать материал как непрерывную среду и применять методы математического анализа. Однородность – это независимость свойств материала от величины выделенного объема (или одинаковость свойств во всех точках). Изотропность – это одинаковость свойств материала во всех направления. Если свойства материала различны в разных направлениях, то материал называется анизотропным (дерево, фанера, ткань).
Далее будем считать материал как сплошное, однородное деформируемое тело, то есть изменяющее свою форму и размеры под действием внешних нагрузок.
Модель материала наделяют свойствами упругости, пластичности и ползу-
чести
Упругостью называется свойство тела восстанавливать свою форму после снятия внешних нагрузок.
Пластичностью называется свойство тела сохранять после прекращения действия нагрузки полностью или частично полученную при нагружении, деформацию.
Ползучестью называется свойство тела увеличивать деформацию при постоянных внешних нагрузках.
Модели формы
Геометрическая форма элементов конструкций очень разнообразна и разной сложности, поэтому находят применение разные модели формы (рис 1.2.).
Рис.1.2. Основные модели формы в моделях прочностной надежности: а) брус, б) пластина, в) оболочка
1.Брус – это модель формы, одно измерение которой много больше двух других. В зависимости от вида деформирования бруса различают: стержень – это брус, работающий на растяжение; балка – это брус, работающий на изгиб; вал – это брус, работающий на кручение.
2.Оболочка (пластина) – это модель формы, одно измерение которой много меньше двух других.
3.Массивное тело – это модель формы, все три измерения которой имеют, одинаковы порядок длины.
Следует отметить, что выбор той или иной формы определяет степень сложности задачи. Так для бруса все характеристики являются функциями одной переменной; для оболочки – функциями двух переменных; для массивного тела
–функциями трех переменных. В нашем курсе мы ограничимся рассмотрением элементов конструкций, форма которых принимается в виде бруса.
Модели нагружения
Модели нагружения схематизируют внешние нагрузки по величине, характеру распределения (сосредоточенная или распределенная), а также воздействие внешних полей и сред.
Внешние силы, действующие на элемент конструкции, подразделяются на три группы: 1) сосредоточенные силы, 2) распределенные силы, 3) объемные или массовые силы.
Сосредоточенные силы — силы, действующие на небольших участках поверхности детали (давление шарика в подшипнике, давление колеса на рельсы).
Распределенные силы приложены на значительных участках поверхности (снеговая нагрузка, подъемная сила на крыло самолета, давление жидкости и газа на стенки сосуда и т.д).
Объемные или массовые силы приложены каждой частице материала (силы тяжести, электромагнитные силы, силы инерции).
Модели нагружения должны учитывать воздействие полей и сред (температура, коррозия, нейтронное поле).
Модели разрушения
Модели разрушения представляют собой уравнения, связывающие параметры работоспособности элемента конструкции в момент разрушения с параметрами, обеспечивающими прочность. Эти уравнения (условия) называют условиями прочности. Наиболее употребительны следующие модели разрушения:
1.статическое разрушение,
2.длительное статическое разрушение,
3.малоцикловое разрушение,
4.усталостное разрушение.
При малом числе циклов (N<102) развиваются значительные пластические деформации (статическое разрушение), при большом числе циклов (N>105) пластические деформации отсутствуют (усталостное разрушение). В промежуточной области (102<N<105) разрушение носит смешанный характер (малоцикловое

разрушение). Если на элемент конструкции действует высокая температура (для алюминиевых сплавов свыше 200 С0, для стальных и титановых сплавов свыше 400 С0, для жаропрочных сплавов свыше 600 С0), но в этом случае рассматривается так называемая длительная прочность материала.
Конечной целью, которая достигается с помощью моделей, является определение запасов прочности
n Pпред 1.
Pмакс
Здесь Pпред – предельное значение вычисляемого параметра (определяется
по моделям материала и моделям разрушения);
Pмакс – это наибольшее значение вычисляемого параметра в рабочих условиях (определяется по моделям формы и по моделям нагружения).
Уравнения равновесия. Внутренние силовые факторы
Деформации рассматриваемого тела (элементов конструкции) возникают от приложения внешней силы. При этом изменяются расстояния между частицами тела, что в свою очередь приводит к изменению сил взаимного притяжения между ними. Отсюда, как следствие, возникают внутренние усилия.
Известно, что различают силы внешние и силы внутренние. Внешние усилия (нагрузки) – это количественная мера взаимодействия двух различных тел. К ним относятся и реакции в связях. Внутренние усилия – это количественная мера взаимодействия двух частей одного тела, расположенных по разные стороны сечения и вызванные действием внешних усилий. Очевидно, что силы относятся к внешним или к внутренним силам в зависимости от очертания границ объекта.
Рис. 1.3. Силы внешние и внутренние
Если рассматривать объект, ограниченный контуром S1, то силы R1, R2 являются внутренними, если же рассматривать объект, ограниченный контуром S2, то силы R1, R2 являются внешними. При этом реакции связей определяются из известных уравнений статики равновесия твердого тела:
I |
|
J |
|
|
I |
|
|
|
J |
|
|
|
прz Pr |
прz |
Rj |
0 , momz |
M r |
momz |
Rj 0 |
||||
r i |
|
j 1 |
|
|
r i |
|
|
|
j 1 |
|
|
I |
|
J |
|
|
I |
|
|
|
J |
|
|
прx |
Pr прx |
Rj |
0 , momx |
M r |
|
momx |
Rj |
0 |
|||
r i |
|
j 1 |
|
|
r i |
|
|
|
j 1 |
|
|

I |
|
J |
|
I |
|
J |
|
|
|
прy |
Pr |
прy |
Rj |
0 , momy |
M r |
momy |
Rj |
0 |
(1.1) |
r i |
|
j 1 |
|
r i |
|
j 1 |
|
|
|
Здесь I – множество внешних активных сил, J – множество опорных реак-
ций.
Заметим, что система уравнений (1) позволяет определить не более шести опорных реакций . Если реакций опор более шести, то исходная система называется статически неопределимой и для вычисления всех опорных реакций необходимо привлечение дополнительных уравнений. Такая ситуация будет рассмотрена позднее.
Мысленное разрежем брус на две части произвольным сечением А (рис.1.4).
Рис. 1.4. . Метод сечений.
В сечении имеются какие-то внутренние силы, удерживающие систему от разрушения. В общем случае все внутренние силы, распределенные по сечению
по некоторому пока неизвестному закону, приводятся к двум векторам: главному |
||||
вектору сил |
|
и главному моменту вектора сил |
|
, приведенные к какой-либо |
R |
L |
|||
точке поперечного сечения (чаще всего к точке, совпадающей с центром тяжести сечения). Каждый из этих векторов можно разложить на составляющие по осям выбранной системы координат. Шесть компонент этих векторов называются внутренними силовыми факторами. Компоненты главного вектора сил принято обозначать Nz Qx Qy и они имеют следующие названия. Nz – продольная сила,
Qx, Qy – поперечные силы вдоль соответствующих осей координат. Компоненты главного момента вектора сил принято обозначать Mz, Mx, My и они имеют следующие названия: Mz – крутящий момент, Mx, My – изгибающие моменты относительно соответствующих осей координат (см. рис.1.5).
Рис.1.5. Внутренние силовые в сечении бруса
Составим уравнения статики отсеченной части
I |
|
Nz |
0 , |
I |
|
Qx |
прz |
Pr |
прx |
Pr |
|||
r i |
|
|
|
r i |
|
|
I |
|
|
|
I |
|
|
momz M r M z |
0 , momx M r |
|||||
r i |
|
|
|
r i |
|
|
I
0 , прy Pr Qy 0
r i
I
M x 0 , momy M r M y 0 . (1.2)
r i
Здесь r=(i, i+1, ,I) – множество всех активных усилий, расположенных в пределах рассматриваемой отсеченной части конструкции. Из этих уравнений определяются значения внутренних силовых факторов в рассматриваемом сечении. Подобную процедуру можно проделать во многих сечения и выявить изменение внутренних силовых факторов от какого-либо параметра (например, от координаты длины рассматриваемого элемента конструкции). Такие зависимости называются эпюрами внутренних силовых факторов.
Вопросы к лекции.
1.Основные понятия о работоспособности конструкции.
2.Что такое модели прочностной надежности.
3.Основные модели прочностной надежности.
4. Уравнения равновесия статики.
5.Что такое внутренние силовые факторы.
Лекция 2
Понятие о напряжениях. Напряженное состояние в точке.
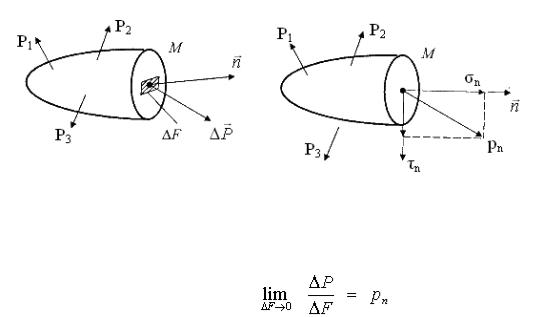
Как отмечалось выше, внутренние силы, действующие в некотором сечении со стороны отброшенной части тела, можно привести к главному вектору и главному моменту. Рассмотрим в сечении точку М, к которой приведены главный вектор внутренних сил и главный момент этих сил. Проведем из этой точки
единичный вектор нормали n . В окрестности этой точки выделим малую пло-
щадку F. Главный вектор внутренних сил, действующих на этой площадке,
обозначим P (рис. 2.1).
Рис.2.1. К определению нормального и касательного напряжений
При уменьшении размеров площадки соответственно уменьшаются главный вектор и главный момент внутренних сил. В пределе при F 0 получим
Введенный таким образом вектор рп называется вектором напряжений в точке. Этот вектор зависит не только от действующих на тело внешних сил и координат рассматриваемой точки, но и от ориентации в пространстве площадки
F, характеризуемой вектором n . Совокупность всех векторов напряжений в точ-
ке М для всевозможных направлений вектора n определяет напряженное состояние в этой точке.

В общем случае направление вектора напряжений рп не совпадает с
направлением вектора нормали n .Проекция вектора рп на направление вектора
n называется нормальным напряжением σn, а проекция на плоскость, проходя-
щую через точку М и ортогональную вектору n – касательным напряжением τn. Деформации тела характеризуются изменением взаимного расположения точек тела до и после деформации. Рассмотрим, например, точку М и близкую к
ней точку N, расстояние между которыми в недеформированном состоянии вдоль направления вектора s обозначим через s (рис. 2.2).
Рис.2.2. К определению линейной деформации
В деформированном состоянии точки М и N переместятся в новое положение (точки М' и N’), расстояние между которыми обозначим через s'. Предел отношения
называется относительной линейной деформацией в точке М в направлении вектора s. Рассматривая три взаимно перпендикулярных направления, например, вдоль координатных осей Ох, Оу и Oz, получим три компоненты относительных линейных деформаций x , y , z , характеризующих изменение объема тела в про-
цессе деформирования.
Для описания деформаций, связанных с изменением формы тела, рассмотрим точку А и две близкие к ней точки B и C, расположенные в недеформированном состоянии в направлении двух взаимно ортогональных векторов s и r (рис. 3). В деформированном состоянии положение точек обозначим через B’ C'. Деформация сдвига
sr 1sr 2sr
Рис. 2.3. К определению угловой деформации в точке

Здесь 1sr , 2 sr – углы поворота отрезков AB и AC относительно первона-
чальных направлений.
Если заданы три взаимно ортогональных вектора, направленных вдоль координатных осей, то имеются три угловые деформации xy , xz , yz , которые
вместе с тремя линейными деформациями x , y , z полностью определяют деформированное состояние в точке.
Напряженное состояние в точке. Тензор напряжений
Совокупность всех возможных пар векторов п, рп в точке определяет напряженное состояние в данной точке. Однако для полного описания напряженного состояния в точке нет необходимости задавать бесконечное множество направлений вектора п, достаточно определить векторы напряжений на трех взаимно перпендикулярных элементарных площадках. Напряжения на произвольно ориентированных площадках могут быть выражены через эти три вектора напряжений.
Проведем через точку М три взаимно перпендикулярных плоскости с векторами нормалей, направления которых совпадают с направлениями координатных осей. Элементарные площадки образуем дополнительными сечениями, параллельными исходным плоскостям и отстоящими от них на бесконечно малые расстояния dx, dy, dz. В результате в окрестности точки М получим бесконечно малый параллелепипед, поверхность которого образована элементарными площадками dFx=dydz, dFy==dxdz, dFz= dxdy. Векторы напряжений рх, р , pz, действующие на элементарных площадках, показаны на рис. 4.
Рис. 2.4. Равновесие бесконечно-малого параллелепипеда
Разложим каждый вектор напряжений на составляющие вдоль координатных осей (рис. 2.5). На каждой площадке действует одно нормальное напряжение( σx ,или σy, или σz) и два касательных напряжения, нижние индексы в обозначениях которых указывают: первый указывает направление действия напряжения, второй – направление вектора нормали к площадке.
