Lek_11-15_Cher
.pdf
Тема11.
Контроль цилиндрических отверстий с помощью ВН ПВТ с ОП
Контроль цилиндрических отверстий с помощью ВН ПВТ с ОП
Вопросы для самоконтроля
ОК - однородный и изотропный
Соленоид создает ОП 
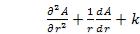– для области 2
– для области 1
Для A из области 1:
1.
2.
– ГУ
Ограниченность.
Неизвестны C1, D1
1.
2.
Вихревые токи
Для расходящейся волны глубина проникновения меньше, чем у плоской или как для цилиндра в соленоиде сходящейся, т.к. расходуется энергия на увеличивающийся фронт расходящейся волны, при x>>1 все 3 кривые сливаются.
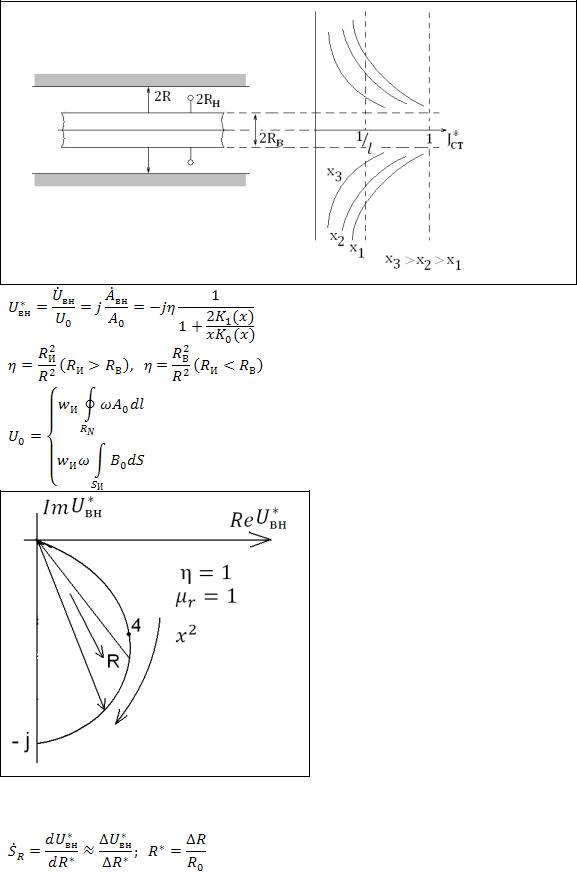
Для немагнитного объекта По линии полуокружности идет проводимость
Уменьшение R увеличивает коэффициент заполнения и 
Тема 12.
Контроль труб внутренними проходными преобразователями с однородным полем
Контроль труб внутренними проходными преобразователями с однородным полем
Зона контроля внутреннего проходного ВТП с однородным полем
Вопросы для самоконтроля
2R1, 2R2 – размеры трубы
Уравнение как для полости и ГУ как для полости + ГУ при r=R1 и ограниченность при 
.
Годографы:
Для тонкостенных труб раздельный контроль невозможен
Uм область |
. Где возм. Разделений |
и T(R1) |
При |
, разделить R, T, невозможно. |
|
Влияют одинаково |
|
|
Чувствительность |
|
|
ведет себя также как чувствительность |
для внешнего радиуса наружного |
|
проходного преобраз. |
|
|
Для трубы:
Наружный ПВТП SнаружR больше
Внутренний ПВТП SвнутрR больше Экранный ПВТП 
больше у других ПВТП.
Зона контроля внутреннего проходного ВТП с однородным полем
– от всех ВТ
Тема13.
Внутренний ПВТП с неоднородным полем
Внутренний ПВТП с неоднородным полем
Вопросы для самоконтроля
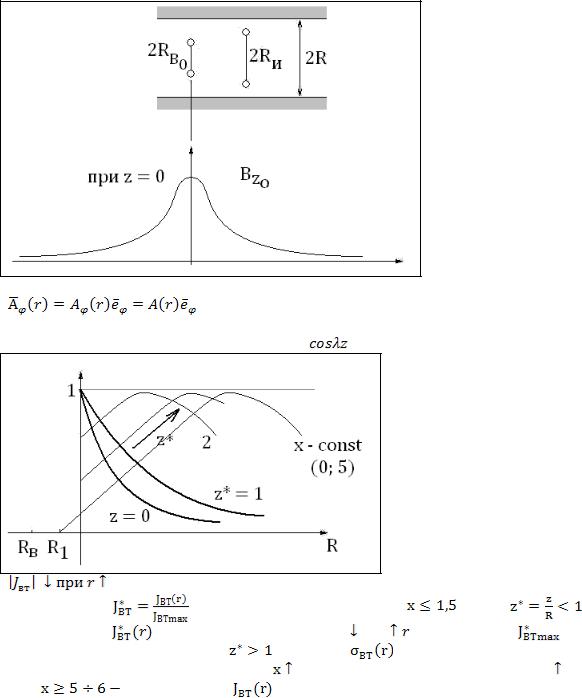
Неоднородность для наружного и внутреннего ВТП проявляется по-разному
Уравнение то же, что и наружный ПВТ, ГУ те же Используем преобразование Фурье с ядром
Распределение |
при разных z, и x = const. Если |
то для |
||
распределение |
имеет стандартный вид, т.е. при |
|
регулярно, т.е. |
|
при r = R (на поверхности). Для |
максимум |
имеет место в |
||
подповерхностных слоях (r > R). Если |
, то зона стандартного распределения и |
|||
при |
распределение |
стандартно при всех z. |
||
Годографы 