- •1. Обозначения
- •2. Модуль (абсолютная величина) действительного числа
- •4. Предел функции
- •5. Бесконечно малые функции и их свойства
- •6. Эквивалентные бесконечно малые. Таблица эквивалентных бесконечно малых
- •7. Бесконечно большие функции и их связь с бесконечно малыми
- •1. Односторонние пределы
- •2. Непрерывность функции в точке
- •3. Производная функции в точке, ее геометрический и механический смысл
- •4. Арифметические действия над производными
- •5. Производная сложной и обратной функций и функции, заданной параметрически
- •6. Производные простейших элементарных функций
- •1. Логарифмическая производная
- •2. Производные и дифференциалы высших порядков
- •3. Формула Тейлора с остаточными членами в форме Пеано и Лагранжа
- •4. Применения формулы Тейлора
- •5. Правило Лопиталя
- •1. Свойства функций, непрерывных на отрезке
- •2. Монотонность функции
- •2. Локальный экстремум
- •3. Выпуклость, вогнутость, точки перегиба
- •4. Исследование функций с помощью высших производных
- •1. Первообразная и неопределенный интеграл
- •2. Замена переменной в неопределенном интеграле
- •3. Интегрирования по частям в неопределенном интеграле
- •4.Выделение полного квадрата
- •5. Определенный интеграл, его свойства и геометрический смысл
- •1. Интеграл с переменным верхним пределом
- •2. Формула Ньютона-Лейбница
- •3. Замена переменных и интегрирование по частям в определенном интеграле
- •4. Интегрирование дробно-рациональных функций
- •4. Интегрирование тригонометрических выражений
- •Лекция 7. Несобственные интегралы первого рода. Приложения интегралов: вычисление площадей, длин дуг и объёмов тел
- •1.Несобственные интегралы
- •2. Вычисление площадей плоских фигур
- •3. Вычисление длины дуги
- •4. Вычисление объёмов тел
1. Первообразная и неопределенный интеграл
Ниже
в качестве
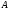 берется любой из промежутков:
берется любой из промежутков: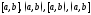 (концы
(концы и
и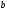 могут быть бесконечными).
могут быть бесконечными).
Определение
1. Говорят,
что функция
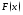 являетсяпервообразной
для функции
являетсяпервообразной
для функции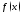 на множестве
на множестве
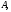 если
если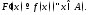 Разыскание всех первообразных функции
Разыскание всех первообразных функции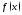 называетсяинтегрированием
называетсяинтегрированием
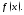
Например,
функция
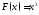 является первообразной для
является первообразной для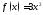 на всей оси
на всей оси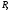 так как
так как
Теорема
1(об
общем виде всех первообразных данной
функции).
Пусть
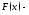 фиксированная
первообразная функции
фиксированная
первообразная функции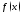 (на множестве
(на множестве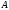 ).
Тогда множество всех первообразных
функции
).
Тогда множество всех первообразных
функции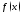 (на множестве
(на множестве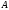 )
описывается формулой
)
описывается формулой
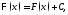
где
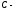 произвольная постоянная.
произвольная постоянная.
Доказательство
вытекает
из того, что если
 и
и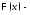 две первообразные функции
две первообразные функции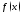 ,
то
,
то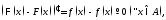 а, значит, разность
а, значит, разность является
постоянной величиной на множестве
является
постоянной величиной на множестве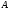 ,
т.е.
,
т.е.
Определение
2. Совокупность
всех первообразных функции
 (на множестве
(на множестве
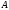 )
называется неопределенным
интегралом на
)
называется неопределенным
интегралом на
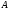 этой функции.
Обозначение:
этой функции.
Обозначение: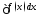 При этом сама функция
При этом сама функция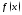 называетсяподынтегральной
функцией и
если интеграл от нее существует, то
говорят, что
называетсяподынтегральной
функцией и
если интеграл от нее существует, то
говорят, что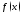 интегрируема
на
интегрируема
на
 .
.
Из
теоремы 1 вытекает, что
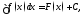 где
где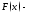 фиксированная
первообразная функции
фиксированная
первообразная функции
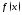 (на множестве
(на множестве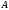 ),
а
),
а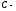 произвольная постоянная.
Отметим, что равенство
произвольная постоянная.
Отметим, что равенство
 равносильно равенству
равносильно равенству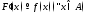 .
Таким образом, для доказательства того,
что некоторая функция
.
Таким образом, для доказательства того,
что некоторая функция является
неопределенным интегралом от функции
является
неопределенным интегралом от функции
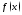 надо продифференцировать ее по
надо продифференцировать ее по если при этом будет получена подынтегральная
функция
если при этом будет получена подынтегральная
функция ,
то равенство
,
то равенство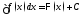 будет истинным.Используя этот факт,
легко докажем следующие формулы.
будет истинным.Используя этот факт,
легко докажем следующие формулы.
Таблица
неопределенных интегралов (ниже везде
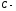 произвольная
постоянная)
произвольная
постоянная)
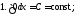

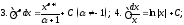
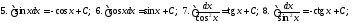
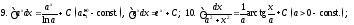
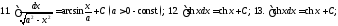
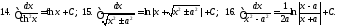
Докажем,
например, формулу 10. Дифференцируем
правую часть равенства 10 по
 :
:
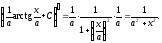
Получена подынтегральная функция левой части 10. Значит, равенство 10 верно. Точно так же доказываются остальные формулы этой таблицы.
Свойства неопределенного интеграла (везде ниже предполагается, что интегралы от соответствующих функций существуют):
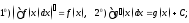
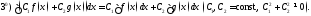
Свойство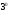 называют свойствомлинейности
интеграла. Первые два свойства
показывают, что операции дифференцирования
и интегрирования взаимно обратны.
называют свойствомлинейности
интеграла. Первые два свойства
показывают, что операции дифференцирования
и интегрирования взаимно обратны.
Немного
позже будет установлено, что всякая
непрерывная на промежутке
 функция
функция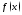 интегрируема на этом промежутке.
интегрируема на этом промежутке.
2. Замена переменной в неопределенном интеграле
Перейдем к формулировке теоремы о замене переменной в неопределенном интеграле, которая часто используется при вычислении интегралов. Здесь имеются в виду два утверждения1:
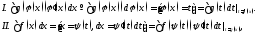
где
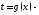 функция, обратная к функции
функция, обратная к функции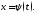
Теорема
2.
а) Пусть выполнены условия: 1) функция
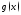 непрерывна в своей области определения
непрерывна в своей области определения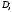 б) функция
б) функция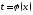 непрерывно дифференцируема на множестве
непрерывно дифференцируема на множестве таком, что
таком, что
 Тогда для всех
Тогда для всех
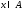 имеет место равенство
имеет место равенство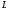
б) Пусть
выполнены условия: 1) функция
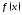 непрерывна в своей области определения
непрерывна в своей области определения
2) функции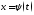 и
и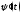 непрерывны на множестве
непрерывны на множестве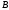 таком, что
таком, что
3)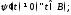 4) функция
4) функция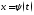 имеет на множестве
имеет на множестве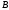 обратную
функцию
обратную
функцию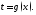 Тогда для всех
Тогда для всех
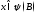 имеет место равенство
имеет место равенство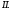
Замечание
1. Преобразования в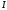 часто называютпроцедурой введения
множителя под знак дифференциала.Формулу
часто называютпроцедурой введения
множителя под знак дифференциала.Формулу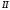 удобно применять в тех случаях, когда
функция
удобно применять в тех случаях, когда
функция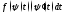 легче интегрируется, чем исходная
функция
легче интегрируется, чем исходная
функция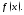 Её применяют, например, при вычислении
интегралов от иррациональностей вида
Её применяют, например, при вычислении
интегралов от иррациональностей вида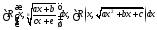 (здесь
(здесь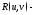 рациональная
функция). В первом случае делается
замена
рациональная
функция). В первом случае делается
замена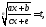 во втором случае подбирают такую замену
во втором случае подбирают такую замену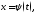 чтобы исчезла иррациональность. Например,
чтобы исчезла иррациональность. Например,
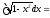
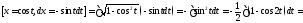
=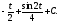 Далее
надо вернуться к старой переменной с
помощью обратной функции
Далее
надо вернуться к старой переменной с
помощью обратной функции и получить ответ:
и получить ответ: