
- •1. Обозначения
- •2. Модуль (абсолютная величина) действительного числа
- •4. Предел функции
- •5. Бесконечно малые функции и их свойства
- •6. Эквивалентные бесконечно малые. Таблица эквивалентных бесконечно малых
- •7. Бесконечно большие функции и их связь с бесконечно малыми
- •1. Односторонние пределы
- •2. Непрерывность функции в точке
- •3. Производная функции в точке, ее геометрический и механический смысл
- •4. Арифметические действия над производными
- •5. Производная сложной и обратной функций и функции, заданной параметрически
- •6. Производные простейших элементарных функций
- •1. Логарифмическая производная
- •2. Производные и дифференциалы высших порядков
- •3. Формула Тейлора с остаточными членами в форме Пеано и Лагранжа
- •4. Применения формулы Тейлора
- •5. Правило Лопиталя
- •1. Свойства функций, непрерывных на отрезке
- •2. Монотонность функции
- •2. Локальный экстремум
- •3. Выпуклость, вогнутость, точки перегиба
- •4. Исследование функций с помощью высших производных
- •1. Первообразная и неопределенный интеграл
- •2. Замена переменной в неопределенном интеграле
- •3. Интегрирования по частям в неопределенном интеграле
- •4.Выделение полного квадрата
- •5. Определенный интеграл, его свойства и геометрический смысл
- •1. Интеграл с переменным верхним пределом
- •2. Формула Ньютона-Лейбница
- •3. Замена переменных и интегрирование по частям в определенном интеграле
- •4. Интегрирование дробно-рациональных функций
- •4. Интегрирование тригонометрических выражений
- •Лекция 7. Несобственные интегралы первого рода. Приложения интегралов: вычисление площадей, длин дуг и объёмов тел
- •1.Несобственные интегралы
- •2. Вычисление площадей плоских фигур
- •3. Вычисление длины дуги
- •4. Вычисление объёмов тел
4. Интегрирование тригонометрических выражений
Интегралы
типа
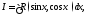 где
где дробно-рациональная
функция пе-
дробно-рациональная
функция пе-
ременных
 и
и ,
сводятся к интегрированию рациональной
функции одной переменной
,
сводятся к интегрированию рациональной
функции одной переменной
с
помощью универсальной
подстановки
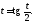 Действительно, тогда
Действительно, тогда
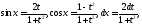
поэтому
 где
где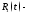 дробно-рациональная функция одной
переменной. К последнему интегралу
можно уже применить алгоритм разложения
на простейшие дроби и свести дело к
интегрированию простейших дробей типа
дробно-рациональная функция одной
переменной. К последнему интегралу
можно уже применить алгоритм разложения
на простейшие дроби и свести дело к
интегрированию простейших дробей типа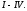 Однако не всегда удобно пользоваться
универсальной подстановкой, так как
она часто приводит к громоздким выкладкам.
Иногда удобнопользоваться
частными типами подстановок, которые
мы приводим ниже.
Однако не всегда удобно пользоваться
универсальной подстановкой, так как
она часто приводит к громоздким выкладкам.
Иногда удобнопользоваться
частными типами подстановок, которые
мы приводим ниже.
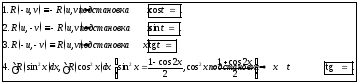 И,
наконец, интегралы типа
И,
наконец, интегралы типа
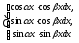
преобразуются в интегралы от синусов и косинусов с помощью формул тригонометрии:
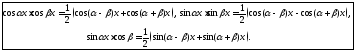
Вычислим, например, интегралы:
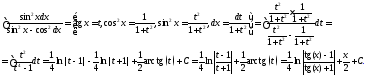
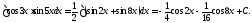
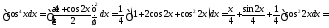
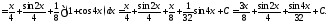
Лекция 7. Несобственные интегралы первого рода. Приложения интегралов: вычисление площадей, длин дуг и объёмов тел
Ранее
рассматривались интегралы
 с конечными пределами
с конечными пределами и от ограниченных функций
и от ограниченных функций Если хотя бы одно из этих ограничений
нарушается, то указанный
Если хотя бы одно из этих ограничений
нарушается, то указанный
интеграл будет несобственным. Такие интегралы часто встречаются в приложениях, поэтому перейдем к их изучению.
1.Несобственные интегралы
Сначала рассмотрим интегралы с бесконечными пределами.
Определение
1. Пусть
функция
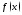 интегрируема на любом отрезке
интегрируема на любом отрезке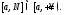 Тогда если существует конечный предел
Тогда если существует конечный предел то говорят, что интеграл
то говорят, что интеграл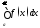 сходится.
При этом пишут
сходится.
При этом пишут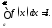 Если же указанный предел не существует
или равен бесконечности, то говорят,
что интеграл
Если же указанный предел не существует
или равен бесконечности, то говорят,
что интеграл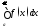 расходится.
расходится.
Аналогично определяются интегралы


(
здесь
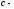 произвольная
конечная точка). Эти интегралы называютнесобственными
интегралами первого рода.
Их геометрический смысл ясен из рис.
11, где площадь
произвольная
конечная точка). Эти интегралы называютнесобственными
интегралами первого рода.
Их геометрический смысл ясен из рис.
11, где площадь
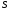
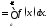 Теперь рассмотрим интегралы от
неограниченных функций.
Теперь рассмотрим интегралы от
неограниченных функций.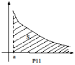
Определение
2. Если
функция
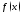 не ограничена в окрестности точки
не ограничена в окрестности точки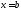 (ее
называютособой
точкой
) и является интегрируемой на любом
отрезке
(ее
называютособой
точкой
) и является интегрируемой на любом
отрезке
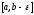
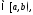 то по определению полагают
то по определению полагают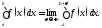 Если этот предел существует и конечен,
то говорят, что интеграл
Если этот предел существует и конечен,
то говорят, что интеграл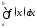 второго
рода
сходится. В противном случае он называется
расходящимся. Аналогичный смысл имеют
интегралы (второго рода)
второго
рода
сходится. В противном случае он называется
расходящимся. Аналогичный смысл имеют
интегралы (второго рода)
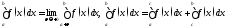 ,
,
где
в первом случае точка
 является особой, а во втором случае
точка
является особой, а во втором случае
точка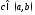 является особой. Поскольку заменой
переменной
является особой. Поскольку заменой
переменной интеграл второго рода
интеграл второго рода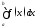
( особая
точка) сводится к интегралу первого
рода, то будем изучать только интегралы
с бесконечным верхним пределом. Сначала
покажем, чтоэталонный
интеграл
особая
точка) сводится к интегралу первого
рода, то будем изучать только интегралы
с бесконечным верхним пределом. Сначала
покажем, чтоэталонный
интеграл

Действительно, имеем
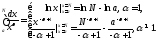
Переходя
здесь к пределу при
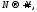 получаем наше утверждение. С помощью
эталонного интеграла можно исследовать
сходимость других несобственных
интегралов.
получаем наше утверждение. С помощью
эталонного интеграла можно исследовать
сходимость других несобственных
интегралов.
Теорема
сравнения 1. Пусть
функции
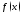 и
и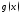 интегрируемы на произвольном отрезке
интегрируемы на произвольном отрезке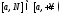 и имеют место неравенства
и имеют место неравенства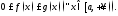 Тогда если сходится интеграл
Тогда если сходится интеграл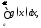 то и сходится интеграл
то и сходится интеграл Если же интеграл
Если же интеграл расходится, то и расходится интеграл
расходится, то и расходится интеграл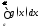
Теорема
сравнения 2.
Пусть функции
 и
и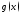 положительны
и
интегрируемы на произвольном отрезке
положительны
и
интегрируемы на произвольном отрезке
 Пусть, кроме того, существует предел
Пусть, кроме того, существует предел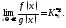 Тогда интегралы
Тогда интегралы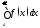 и
и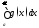 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Замечание 1. При применении этих теорем часто используется таблица эквивалентных бесконечно малых:
Если
 при
при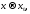 то при
то при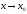 верны
следующие соотношения:
верны
следующие соотношения:
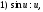
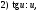

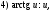
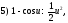
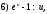
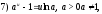
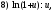
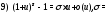 const.
const.
Например,
интеграл
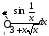 сходится, так как
сходится, так как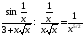 и интеграл
и интеграл сходится (см. эталонный интеграл(
сходится (см. эталонный интеграл( ) и теорему сравнения 2).
) и теорему сравнения 2).
Отметим,
что теоремы сравнения верны лишь для
неотрицательных подынтегральных
функций. Если эти функции не являются
знакопостоянными, то вводят понятие
абсолютной сходимости: говорят, что
интеграл
 сходится абсолютно,
если сходится интеграл
сходится абсолютно,
если сходится интеграл
 Если последний интеграл расходится, а
сам интеграл
Если последний интеграл расходится, а
сам интеграл сходится, то его называютусловно
сходящимся интегралом.
Нетрудно показать,
что
из сходимости интеграла
сходится, то его называютусловно
сходящимся интегралом.
Нетрудно показать,
что
из сходимости интеграла
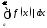 вытекает обычная сходимость интеграла
вытекает обычная сходимость интеграла
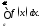 Обратное, вообще говоря, неверно. Можно
показать, например, что интеграл
Обратное, вообще говоря, неверно. Можно
показать, например, что интеграл
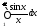 сходится,
а интеграл
сходится,
а интеграл
 расходится. Тем не менее, при исследовании
сходимости интегралов от знакопеременных
функций изучают сначала их абсолютную
сходимость (здесь можно применить
теоремы сравнения), а затем – условную
сходимость.
расходится. Тем не менее, при исследовании
сходимости интегралов от знакопеременных
функций изучают сначала их абсолютную
сходимость (здесь можно применить
теоремы сравнения), а затем – условную
сходимость.
Например,
рассмотрим интеграл
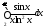 .
Здесь подынтегральная функция изменяет
знак на полуинтервале
.
Здесь подынтегральная функция изменяет
знак на полуинтервале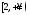 ,
поэтому применить к нему теоремы
сравнения нельзя. Рассмотрим “модульный”
интеграл
,
поэтому применить к нему теоремы
сравнения нельзя. Рассмотрим “модульный”
интеграл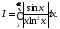 Здесь подынтегральная функция
неотрицательна, и поэтому к этому
интегралу можно применить теорему
сравнения 1:
Здесь подынтегральная функция
неотрицательна, и поэтому к этому
интегралу можно применить теорему
сравнения 1:
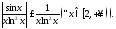
Так
как интеграл
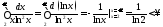 сходится, то и интеграл
сходится, то и интеграл также сходится, а, значит, исходный
интеграл
также сходится, а, значит, исходный
интеграл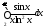 сходится
абсолютно.
сходится
абсолютно.
