2. Вычисление площадей плоских фигур

Из геометрического смысла определенного интеграла вытекает следующее утверждение.

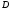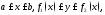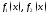Теорема 1. Если фигура задана неравенствамигде функциинепрерывны на отрезке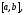то площадь этой фигуры вычисляется по

формуле 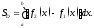Если фигура ограничена линиями 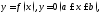причем функциязнакопеременна и непрерывна на отрезке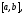то её площадь равна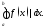

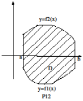
Действительно, фигуру можно перенести параллельно оси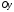вверх и тогда она будет сверху и снизу ограничена линиями

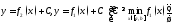
Поэтому

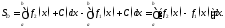
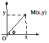
Переходя к вычислению площади в полярных координатах, напомним, что любая точка

на плоскости вполне однозначно определяется своим полярным радиусом

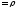и полярным углом 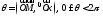(считаем, что началу координат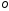соответствует радиуси любой фиксированный полярный угол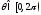). Поэтому любую кривую на плоскости можно задать уравнением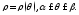Переход от декартовых координат точки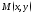к полярным осуществляется по формулам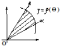

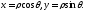
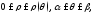Теорема 2. Пусть фигура задана в полярных координатах неравенствамипричем функциянепрерывна на отрезке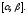Тогда площадь этой фигуры вычисляется по формуле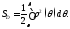Если фигура описывается неравенствами

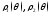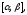причем функции непрерывны на отрезкето её площадь вычисляется по формуле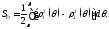

Площади фигур с замкнутой границей удобно вычислять, если граница задана в параметрической форме.

Теорема 3. Пусть фигура 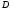имеет границу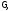заданную параметрически уравнениями

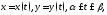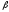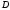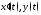причем при возрастании параметра откобход границысовершается так, что сама областьостается слева от наблюдателя. Если при этом функциинепрерывны на отрезке, то площадь этой фигуры вычисляется по формуле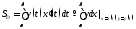

3. Вычисление длины дуги

Пусть на плоскости задана некоторая незамкнутая кривая(см. рис. Р16). Произведем разбиение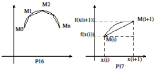

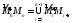
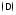
этой дуги на частичные дуги 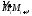в каждую из которых впишем хорду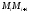. Тогда получим ломанную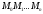, вписанную в дугу. Пусть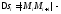длина хорды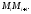

Определение 3. За длину дуги 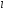кривойпринимают предел, к которому стремится периметр ломанной, вписанной в эту дугу, при стремлении длины максимального звена этой ломанной к нулю, т. е.Если криваязамкнутая, то разбивают ее двумя несовпадающими точками на две незамкнутые кривые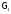ии тогда

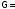дл.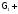дл.дл.

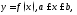Теорема 4. Если дуга задана уравнениемгде функция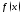непрерывно дифференцируема на отрезк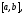ето ее длина вычисляется по формуле

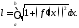
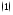
Доказательство. Произведем разбиение 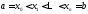отрезка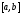на частичные отрезки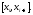Это разбиение порождает разбиениедугичастичные дугиПо определению 3 имеем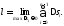Длина хорды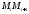равна (см. рис. Р17) величине

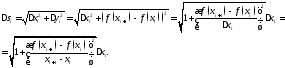
По теореме Лагранжа существует точка такая, что

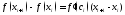
поэтому 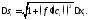Учитывая это, получаем, что

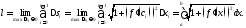
Теорема доказана.

Замечание 2. Величина 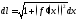называетсядифференциалом дуги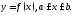Учитывая, что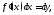её можно записать в виде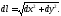Мы получили теорему Пифагора для криволинейного треугольника с катетами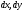и “гипотенузой”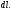Теперь формулу (1) для вычисления длины дуги можно записать кратко так: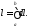Эта форма записи длины дуги особенно удобна, если дугазадана параметрически или в полярной форме. Из нее можно получить следующие утверждения.

Теорема 5. Если дуга задана параметрически уравнениями 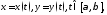где функции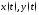непрерывно дифференцируемы на отрезк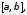ето ее длина вычисляется по формуле

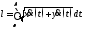
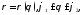Если дуга задана в полярных координатах уравнениемгде функция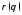непрерывно дифференцируема на отрезке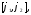то её длина вычисляется по формуле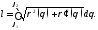

Действительно, если задана в параметрической форме, то

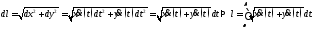
Рекомендуем получить формулу длины дуги в полярных координатах самостоятельно.

Например, если дуга задана уравнениемто её длина равна