
- •1. Обозначения
- •2. Модуль (абсолютная величина) действительного числа
- •4. Предел функции
- •5. Бесконечно малые функции и их свойства
- •6. Эквивалентные бесконечно малые. Таблица эквивалентных бесконечно малых
- •7. Бесконечно большие функции и их связь с бесконечно малыми
- •1. Односторонние пределы
- •2. Непрерывность функции в точке
- •3. Производная функции в точке, ее геометрический и механический смысл
- •4. Арифметические действия над производными
- •5. Производная сложной и обратной функций и функции, заданной параметрически
- •6. Производные простейших элементарных функций
- •1. Логарифмическая производная
- •2. Производные и дифференциалы высших порядков
- •3. Формула Тейлора с остаточными членами в форме Пеано и Лагранжа
- •4. Применения формулы Тейлора
- •5. Правило Лопиталя
- •1. Свойства функций, непрерывных на отрезке
- •2. Монотонность функции
- •2. Локальный экстремум
- •3. Выпуклость, вогнутость, точки перегиба
- •4. Исследование функций с помощью высших производных
- •1. Первообразная и неопределенный интеграл
- •2. Замена переменной в неопределенном интеграле
- •3. Интегрирования по частям в неопределенном интеграле
- •4.Выделение полного квадрата
- •5. Определенный интеграл, его свойства и геометрический смысл
- •1. Интеграл с переменным верхним пределом
- •2. Формула Ньютона-Лейбница
- •3. Замена переменных и интегрирование по частям в определенном интеграле
- •4. Интегрирование дробно-рациональных функций
- •4. Интегрирование тригонометрических выражений
- •Лекция 7. Несобственные интегралы первого рода. Приложения интегралов: вычисление площадей, длин дуг и объёмов тел
- •1.Несобственные интегралы
- •2. Вычисление площадей плоских фигур
- •3. Вычисление длины дуги
- •4. Вычисление объёмов тел
1. Односторонние пределы
Дадим их кратко.
Определение
1. Левый
предел
функции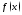 в точке
в точке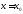 (обозначение:
(обозначение: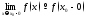 ):
):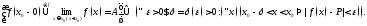
Правый
предел
функции в точке
в точке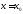 (обозначение:
(обозначение: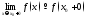 ):
):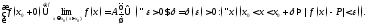 Очевидно следующее свойство:
Очевидно следующее свойство:
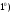 Для
существования обычного предела
Для
существования обычного предела
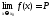 необходимо и достаточно, чтобы существовали
односторонние пределы
необходимо и достаточно, чтобы существовали
односторонние пределы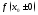 и чтобы имело место равенство
и чтобы имело место равенство
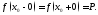
2. Непрерывность функции в точке
Пусть
функция
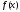 определена в точке
определена в точке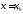 и некоторой ее окрестности.
и некоторой ее окрестности.
Определение
2.
Функция
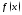 называетсянепрерывной
в точке
называетсянепрерывной
в точке
 если
если
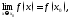 т.е.
если
т.е.
если
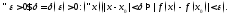
Функция
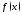 называетсянепрерывной
слева (справа) в точке
называетсянепрерывной
слева (справа) в точке
 если
если
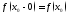 (соответственно
(соответственно
 ).
).
Функция
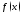 называетсянепрерывной
на множестве
называетсянепрерывной
на множестве
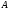 если она непрерывна в каждой точке
если она непрерывна в каждой точке
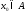 этого множества.
этого множества.
Очевидны следующие высказывания.
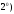 (
(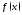 непрерывна
в точке
непрерывна
в точке
 )
)
 Для
того чтобы функция
Для
того чтобы функция
 была непрерывна в точке
была непрерывна в точке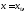 необходимо
и достаточно, чтобы она была непрерывна
слева и справа в точке
необходимо
и достаточно, чтобы она была непрерывна
слева и справа в точке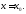
Нетрудно
показать, что
сумма, разность и произведение двух
функций, непрерывных в точке
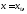 также являются непрерывными в этой
точке функциями.
Частное
также являются непрерывными в этой
точке функциями.
Частное
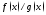 двух непрерывных в точке
двух непрерывных в точке функций непрерывно в этой точке, если
функций непрерывно в этой точке, если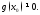
С непрерывными функциями связаны следующие два важных утверждения.
Теорема
1.
Пусть
сложная функция
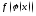 определена в некоторой проколотой
окрестности точки
определена в некоторой проколотой
окрестности точки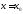 и пусть выполнены условия:
и пусть выполнены условия:
а)
существует

б)
функция
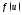 непрерывна в точке
непрерывна в точке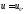
Тогда
существует предел
 и имеет место равенство
и имеет место равенство
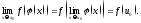
Теорема
2.
Пусть
сложная функция
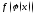 определена в точке
определена в точке и некоторой ее окрестности и пусть
выполнены условия:
и некоторой ее окрестности и пусть
выполнены условия:
а)
функция
 непрерывна в точке
непрерывна в точке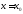 ,
,
б)
функция
 непрерывна в соответствующей точке
непрерывна в соответствующей точке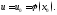
Тогда
сложная функция
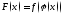 непрерывна в точке
непрерывна в точке
Теорему 1 называют теоремой о переходе к пределу под знаком непрерывной функции, а теорему 2– теоремой о непрерывности сложной функции.
Пример
1. Найти предел
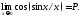
Решение.
Так как существует
 а функция
а функция непрерывна в точке
непрерывна в точке то по теореме 1 имеем
то по теореме 1 имеем

Определение 3.Функции вида
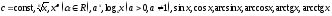
называются простейшими элементарными функциями. Всякая функция, полученная из простейших элементарных функций путем применения к ним конечного числа операций сложения, вычитания, умножения, деления и взятия функций от функций (т.е. образования сложных функций) называется элементарной функцией (общего вида).
Имеет место следующая замечательная теорема.
Теорема
3.
Всякая
элементарная функция
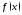 непрерывна в любой внутренней точке
своей области определения
непрерывна в любой внутренней точке
своей области определения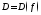 .
.
Напомним,
что точка
 называетсявнутренней
точкой множества
называетсявнутренней
точкой множества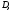 если она входит в
если она входит в
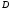 вместе с некоторой своей окрестностью
вместе с некоторой своей окрестностью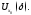
Например,
функция
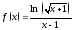 непрерывна на множестве
непрерывна на множестве так как это множество является областью
определения функции
так как это множество является областью
определения функции и все точки этого множества – внутренние.
и все точки этого множества – внутренние.
Если
хотя бы одно из условий определения 2
не выполнено, то функция
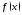 является
является
разрывной
в точке
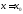 .
Различают два типа разрывов:
.
Различают два типа разрывов:
Точка –
точка
разрыва I
рода:
а) существуют
–
точка
разрыва I
рода:
а) существуют и конечные односторонние пределы
и конечные односторонние пределы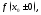 но либо они не совпадают, либо хотя бы
один из них не равен значению
но либо они не совпадают, либо хотя бы
один из них не равен значению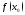 ;
;
б)
существуют конечные односторонние
пределы
 но
но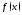 не определена в точке
не определена в точке
Точка –
точка
разрыва II
рода:
либо не существует хотя бы один из
односторонних пределов
–
точка
разрыва II
рода:
либо не существует хотя бы один из
односторонних пределов
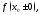 либо
хотя бы один из них равен бесконечности.
либо
хотя бы один из них равен бесконечности.
Например,
точка
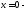 точка разрываI
рода для функций
точка разрываI
рода для функций
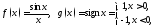
а
для функции
 она является точкой разрываII
рода.
она является точкой разрываII
рода.
Если
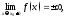 то
прямая
то
прямая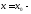 вертикальная
асимптота для функции
вертикальная
асимптота для функции Прямая
Прямая
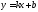 называется наклонной (горизонтальной
при
называется наклонной (горизонтальной
при )
асимптотой
функции
)
асимптотой
функции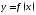 ,если
,если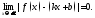 Нетрудно
показать, что если существуют конечные
пределы
Нетрудно
показать, что если существуют конечные
пределы

то
прямая
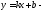 асимптота
кривой
асимптота
кривой
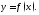 Таким
образом, асимптоты функции
Таким
образом, асимптоты функции
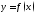 могут
возникнуть при подходе
могут
возникнуть при подходе
 к точкам разрыва
к точкам разрыва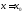 второго
рода этой функции либо на бесконечности.
второго
рода этой функции либо на бесконечности.
