4. Вычисление объёмов тел

С помощью определенного интеграла можно вычислять и объёмы тел. Дадим соответствующие формулы.

Теорема 6. Пусть тело заключено между плоскостямииаплощадь его поперечного сечения плоскостьюЕсли функциянепрерывна на отрезкето объём телавычисляется по формуле

Замечание 3. Если тело получено вращением криволинейной трапеции

вокруг оси , то объём этого тела вычисляется по формуле

Действительно, в этом случае поперечное сечение является кругом радиуса поэтомуАналогично вычисляется объём тела, полученного вращением вокруг осикриволинейной трапеции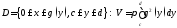(конечно, в выписанных формулах дляпредполагается, что функцииинепрерывны на соответствующих отрезках).

1Здесь и всюду далее с тем, чтобы не прерывать выкладки, в квадратных скобках будем указывать соответствующие замены переменных или формулы, необходимые для преобразований исходных выражений.

2На рис. Р6: – это трапеция ограниченная сверху кривой снизу– осью , с боков– прямыми и

71