19.Уравнение прямой в пространстве.

20 Вопрос: Кривые II порядка.

21 Вопрос: Поверхности II порядка. Уравнения поверхностей второго порядка

Эллипсоид a, b, c — полуоси
Сфера (частный случай эллипсоида)
Однополостный гиперболоид c — действительная полуось, a и b — мнимые полуоси
Двуполостный гиперболоид c — действительная полуось, a и b — мнимые полуоси
Конус Вершина конуса в начале координат, направляющая кривая — эллипс с полуосями а и b, плоскость которого находится на расстоянии с от начала координат
Эллиптический параболоид
Гиперболический параболоид
Эллиптический цилиндр a и b — полуоси
Гиперболический цилиндр
Параболический цилиндр p — фокальный параметр

22 Вопрос: Действия с матрицами. Определители второго и третьего порядка.

Определение. Матрицей размера называется прямоугольная таблица из чисел, где,,

,

состоящая из строк истолбцов.

Определение. Суммой матрициразмераназывается матрицатого же размера, каждый элемент которой равен сумме соответствующих элементов матрицА и В: ,,.

Определение. Произведением αА матрицы на число α называется матрица, элементы которой.

Пример 7. Вычислить 3А+2В, если

, .

Решение. Вычислим ,. Тогда.

Определение. Произведением АВ матрицы размерана матрицуразмераназывается матрицаразмера, элемент которой, стоящий в i-ой строке и j-ом столбце, равен сумме произведений соответствующих элементов i-ой строки матрицы А и j-ого столбца матрицы В:

,

.

Так как строки и столбцы матриц участвуют в произведении АВ неравноправно, то АВ≠ВА.

Пример 8. Вычислить .

Решение. Умножим элементы первой строки первой матрицы на соответствующие элементы первого столбца второй матрицы и сложим все произведения. Полученный элемент поставим в первую строку и первый столбец матрицы-произведения. Далее вычислим остальные элементы произведения матриц.

.

Матрицу называют единичной. Легко проверить, что, если, конечно, число столбцов матрицыА равно числу строк матрицы Е, и ЕА=А.

Если матрица А имеет одинаковое число строк и столбцов, то ее называют квадратной.

Определение. Определителем квадратной матрицы А называется определитель, составленный из ее элементов.

Обозначают определитель матрицы А либо det A (от слова детерминант, т.е. определитель), либо |A|, либо D.

Определение. Квадратная матрица А называется невырожденной, если ее определитель отличен от нуля. В противном случае матрицу называют вырожденной.

Определение. Матрица такая, что, называется обратной матрицеА.

Если А – невырожденная матрица, то существует и при этом единственная матрица, обратная к матрице А. При этом 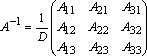, где- алгебраические дополнения к элементам исходной матрицы.

Замечание. Следует обратить внимание на то, что алгебраические дополнения к элементам строк матрицы А располагают в столбцах с теми же номерами, что и строки данной матрицы А.

Пример 9. Найти матрицу, обратную к матрице .

Решение. Вычислим 

Найдем алгебраические дополнения соответствующих элементов матрицы А:

, ,

 ,

, ,

 ,

, ,

.

Имеем .

22.2 Определители 2 и 3 порядка.

Определителем называется число, записанное в виде квадратной таблицы:

 .

 

Таблица ограничивается слева и справа вертикальными линиями,  -называется элементами определителя ( -номер строки,  -номер столбца).

Главная диагональ определителя содержит элементы  , противоположная диагональ называется побочной.

Порядком определителя называется число строк (столбцов) квадратной таблицы.

Определитель II порядка вычисляется по формуле:

 

Определитель III порядка можно вычислить по правилу Сарруса:

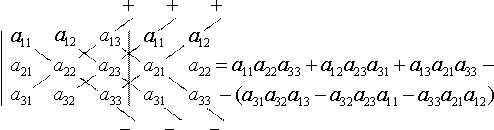
Основные свойства определителей:

1.1. Значение определителя не изменится, если:

- строки заменить на столбцы, такое действие называется транспонирование, т.е. действия, выполняемые со строками, справедливы и для столбцов;

- все элементы одной строки умножить на какое-либо число и прибавить к соответствующим элементам другой строки.

Такие действия с элементами определителя называются элементарными преобразованиями.

1.2. Определитель меняет знак на противоположный, если две каких-либо строки поменять местами.

1.3. Определитель равен нулю, если:

- все элементы какой-либо строки равны нулю;

- соответствующие элементы каких-либо двух строк равны;

- соответствующие элементы каких-либо двух строк пропорциональны.

2. Алгебраическое дополнение и минор.  Элементарные преобразования.  Вычисление определителей n-го порядка (n >4)

Минором  к элементу  называется определитель, полученный из исходного, вычеркиванием  -й  строки и  -го столбца.

Таким образом, порядок минора меньше порядка исходного определителя на единицу.

Алгебраическое дополнение  – минор  с соответствующим знаком, т.е.

 .

Вычисление определителей n-го порядка выполняется по формуле:

т.е. определитель представляется в виде разложения по элементам  -й строки.

Пример

Вычислить определитель IV порядка: