1 Вопрос: Предел функции в точке. Геометрический смысл. Односторонние пределы.

1.1. Предел функции. Геометрический смысл.

Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Выясним, в чём заключается геометрический смысл предела функции в точке. Построим график функции  и отметим на нём точки  и .

Предел функции  в точке  существует и равен , если для любой -окрестности точки  можно указать такую -окрестность точки , что для любого  из этой -окрестности значение  будет находится в -окрестности точки .

Отметим, что по определению предела функции в точке для существования предела при не важно, какое значение принимает функция в самой точке . Можно привести примеры, когда функция не определена при или принимает значение, отличное от . Тем не менее, предел может быть равен .

1.2. Односторонние пределы

В   определении   предела   функции считается, что х стремится к x₀ любым способом: оставаясь меньшим, чем x₀ (слева от х₀), большим, чем х_о (справа от х_о), или колеблясь около точки x₀.

Бывают случаи, когда способ приближения аргумента х к х_о существенно влияет на значение придела  функции. Поэтому вводят понятия односторонних пределов.

Число А₁ называется пределом функции у=ƒ(х) слева в точке х_о, если для любого число ε>0 существует число δ=δ(ε)> 0 такое, что при х є (х₀-δ;x_o), выполняется неравенство |ƒ(х)-А|<ε. Предел слева записывают так: limƒ(х)=А при х–>х₀-0 или коротко: ƒ(х_о-0)=А₁ (обозначение Дирихле) (см. рис. 111).

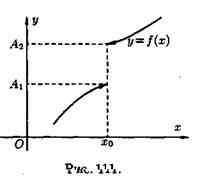
Аналогично определяется предел функции справа, запишем его с помощью символов:

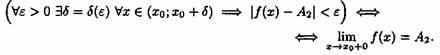
Коротко предел справа обозначают ƒ(х_о+0)=А.

Пределы функции слева и справа называются односторонними пределами. Очевидно, если существует  , то существуют и оба односторонних предела, причем А=А₁=А₂.

Справедливо и обратное утверждение: если существуют оба предела ƒ(х₀-0) и ƒ(х₀+0) и они равны, то существует предел  и А=ƒ(х₀-0).

Если же А₁А₂, то этот придел не существует.

2 Вопрос: Бесконечно малые функции и их свойства. Эквивалентные бесконечно малые. Бесконечно большие функции. Вертикальные асимптоты графика функции.

2.1. Бесконечно малые и их свойства.

Функция α(х) называется бесконечно малой при   , если ,  

т. е. для любого числа ε > 0 существует такое число δ > 0, что для всех х, удовлетворяющих неравенству 

, 

выполняется неравенство 

 . 

 

Бесконечно малую функцию α(х) называют бесконечно малой величиной или просто  бесконечно малой.  

Функция f (х) называется ограниченной при , если существуют положительные числа М и δ, такие, что при условии  , выполняется неравенство   .  

 

Например, любая бесконечно малая α(х) является  ограниченной функцией при .  

В дальнейшем будем рассматривать  бесконечно малые при .  

Свойства бесконечно малых.  

1. Если функции и являются  бесконечно малыми, то функция также есть бесконечно малая. Это свойство распространяется на случай  алгебраической суммы любого конечного числа бесконечно малых.  

2. Произведение ограниченной при  функции на бесконечно малую есть функция бесконечно малая.  

3. Произведение постоянной на бесконечно малую есть бесконечно малая.  

4. Произведение двух бесконечно малых есть бесконечно малая. Это свойство распространяется на любое  конечное число бесконечно малых.