
- •1 Вопрос: Предел функции в точке. Геометрический смысл. Односторонние пределы.
- •1.2. Односторонние пределы
- •2 Вопрос: Бесконечно малые функции и их свойства. Эквивалентные бесконечно малые. Бесконечно большие функции. Вертикальные асимптоты графика функции.
- •2.1. Бесконечно малые и их свойства.
- •2.2. Эквивалентные бесконечно малые.
- •2.3. Бесконечно большие функции.
- •2.4. Асимптоты графика функции.
- •3 Вопрос: Арифметические действия с пределами. Теоремы о переходе к пределу в неравенствах. Теорема о пределе промежуточной функции.
- •3.1. Арифметические действия с пределами.
- •3.2. Теоремы о переходе к пределу в неравенствах.
- •3.3. Теорема о пределе промежуточной функции.
- •4.1. Первый и второй замечательные пределы.
- •4.3. Горизонтальные и наклонные асимптоты графика функции. Виды асимптот
- •5 Вопрос: Непрерывность функции в точке. Точки разрыва и их классификация.
- •10 Вопрос: Производная сложной функции. Производные и дифференциалы высших порядков. Теорема Ролля, Лагранжа, Коши.
- •11 Вопрос: Правило Лопиталя:
- •12 Вопрос: Условия возрастания и убывания функции:
- •13 Вопрос: Выпуклость графика функции. Точки перегиба.
- •14 Вопрос: Общая схема исследования функций и построения графика. Формула Тейлора.
- •18 Вопрос: Уравнение плоскости в пространстве.
- •19.Уравнение прямой в пространстве.
- •20 Вопрос: Кривые II порядка.
- •21 Вопрос: Поверхности II порядка. Уравнения поверхностей второго порядка
- •22 Вопрос: Действия с матрицами. Определители второго и третьего порядка.
11 Вопрос: Правило Лопиталя:
Теорема
Пусть f(x) и g(x) имеют производную f’(x) и g'(x) ( не равных нулю) в некоторой окресности точки х0 ,кроме быть может самой точки х0 и существ. limf(x) при x-> x0 и limg(x) при x->x0
Теорема Лопиталя:
 либо
либо
 ;
;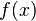 и
и
 дифференцируемы
в проколотой окрестности
дифференцируемы
в проколотой окрестности ;
; в
проколотой окрестности
в
проколотой окрестности
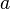 ;
;существует
 ,
,
тогда
существует
![]() .
.
12 Вопрос: Условия возрастания и убывания функции:
Определение возрастающей функции.
Функция
y=f(x)
возрастает на интервале X,
если для любых
![]() и
и![]() выполняется
неравенство
выполняется
неравенство![]() .
Другими словами – большему значению
аргумента соответствует большее значение
функции.
.
Другими словами – большему значению
аргумента соответствует большее значение
функции.
Определение убывающей функции.
Функция
y=f(x)
убывает на интервале X,
если для любых
![]() и
и![]() выполняется
неравенство
выполняется
неравенство![]() .
Другими словами – большему значению
аргумента соответствует меньшее значение
функции.
.
Другими словами – большему значению
аргумента соответствует меньшее значение
функции.
ЗАМЕЧАНИЕ: если функция определена и непрерывна в концах интервала возрастания или убывания (a;b), то есть при x=a и x=b, то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке X.
Первое достаточное условие экстремума
Теорема
(Первое достаточное условие экстремума)
Пусть
для функции
![]() выполнены
следующие условия:
выполнены
следующие условия:
функция непрерывна в окрестности точки
 ;
; или
или
 не
существует;
не
существует;производная
 при
переходе через точку
при
переходе через точку меняет
свой знак.
меняет
свой знак.
Тогда
в точке
![]() функция
функция![]() имеет
экстремум, причем это минимум, если при
переходе через точку
имеет
экстремум, причем это минимум, если при
переходе через точку![]() производная
меняет свой знак с минуса на плюс;
максимум, если при переходе через точку
производная
меняет свой знак с минуса на плюс;
максимум, если при переходе через точку![]() производная
меняет свой знак с плюса на минус.
производная
меняет свой знак с плюса на минус.
Второе достаточное условие экстремума
Теорема
(Второе достаточное условие экстремума)
Пусть
для функции
![]() выполнены
следующие условия:
выполнены
следующие условия:
она непрерывна в окрестности точки
 ;
;первая производная
 в
точке
в
точке ;
; в
точке
в
точке
 .
.
Тогда
в точке
![]() достигается
экстремум, причем, если
достигается
экстремум, причем, если![]() ,
то в точке
,
то в точке![]() функция
функция![]() имеет
минимум; если
имеет
минимум; если![]() ,
то в точке
,
то в точке![]() функция
функция![]() достигает
максимум.
достигает
максимум.
Необходимое условие экстремума
Теорема
(Необходимое условие экстремума)
Если
функция
![]() имеет
экстремум в точке
имеет
экстремум в точке![]() ,
то ее производная
,
то ее производная![]() либо
равна нулю, либо не существует.
либо
равна нулю, либо не существует.
13 Вопрос: Выпуклость графика функции. Точки перегиба.
График
функции ![]() ,
дифференцируемой на интервале
,
дифференцируемой на интервале![]() ,
является на этом интервалевыпуклым,
если график этой функции в пределах
интервала
,
является на этом интервалевыпуклым,
если график этой функции в пределах
интервала ![]() лежит
не выше любой своей касательной (рис.
1).
лежит
не выше любой своей касательной (рис.
1).
График
функции ![]() ,
дифференцируемой на интервале
,
дифференцируемой на интервале![]() ,
является на этом интервалевогнутым,
если график этой функции в пределах
интервала
,
является на этом интервалевогнутым,
если график этой функции в пределах
интервала ![]() лежит
не ниже любой своей касательной (рис.
2).
лежит
не ниже любой своей касательной (рис.
2).

Теоремы о выпуклости функции и точках перегиба
Теорема
(Об условиях выпуклости или вогнутости графика функции)
Пусть
функция ![]() определена
на интервале
определена
на интервале![]() и
имеет непрерывную, не равную нулю в
точке
и
имеет непрерывную, не равную нулю в
точке![]() вторую
производную. Тогда, если
вторую
производную. Тогда, если![]() всюду
на интервале
всюду
на интервале![]() ,
то функция имеетвогнутость
на этом интервале,
если
,
то функция имеетвогнутость
на этом интервале,
если ![]() ,
то функция имеетвыпуклость.
,
то функция имеетвыпуклость.
Определение
Точкой
перегиба графика
функции ![]() называется
точка
называется
точка![]() ,
разделяющая промежутки выпуклости и
вогнутости.
,
разделяющая промежутки выпуклости и
вогнутости.
Теорема
(О необходимом условии существования точки перегиба)
Если
функция ![]() имеет
перегиб в точке
имеет
перегиб в точке![]() ,
то
,
то![]() или
не существует.
или
не существует.
Теорема
(О достаточном условии существования точки перегиба)
Если:
первая производная
 непрерывна
в окрестности точки
непрерывна
в окрестности точки  ;
;вторая производная
 или
не существует в точке
или
не существует в точке ;
; при
переходе через точку
при
переходе через точку  меняет
свой знак,
меняет
свой знак,
тогда
в точке ![]() функция
функция![]() имеет
перегиб.
имеет
перегиб.
Схема исследования функции на выпуклость, вогнутость
Найти вторую производную функции.
Найти точки, в которых вторая производная равна нулю или не существует.
Исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба.
Пример
Задание. Найти
интервалы выпуклости/вогнутости
функции ![]()
Решение. Найдем вторую производную заданной функции:
![]()
Находим
точки, в которых вторая производная
равна нулю, для этого решаем уравнение ![]() :
:
![]()
Исследуем знак второй производной слева и справа от полученной точки:

Так
как на промежутке ![]() вторая
производная
вторая
производная![]() ,
то на этом промежутке функция
,
то на этом промежутке функция![]() выпукла;
в силу того, что на промежутке
выпукла;
в силу того, что на промежутке![]() вторая
производная
вторая
производная![]() -
функция вогнута. Так как при переходе
через точку
-
функция вогнута. Так как при переходе
через точку![]() вторая
производная сменила знак, то эта точка
является точкой перегиба графика
функции.
вторая
производная сменила знак, то эта точка
является точкой перегиба графика
функции.
Ответ. Точка ![]() -
точка перегиба графика функции.
-
точка перегиба графика функции.
На
промежутке ![]() функция
выпукла, на промежутке
функция
выпукла, на промежутке![]() функция
вогнута.
функция
вогнута.
