Otvety_Pchelko_29_30

Контрольная работа № 1(маг.13)

1. Почему практически нельзя выбирать период квантования функции по времени из условия T =1/(2*fмакс.)?

2. Как из квантованного по времени сигнала восстановить исходный непрерывный сигнал?

3. Приведите пример использования свёртки во времени.

4. Дискретная свёртка может быть линейной и круговой. В каких случаях применяют только линейную свёртку, а в каких – только круговую?

5. С какой целью применяют метод секционирования при вычислении линейной свёртки?

6. При вычислении линейной свёртки, какой метод секционирования лучше – с перекрытием или без перекрытия?

7. Имеются две гармонических функции, одна из которых имеет частоту втрое большую, чем у другой. Нарисуйте их дискретное представление f1(n) и f2(n).

8. Как длина круговой свёртки связана с длинами сворачиваемых функций?

9. Покажите математически (не графически), что x(n-k) есть зеркальное отображение функции x(n).

10. Каков алгоритм ускорения вычисления круговой свёртки?

11. В каких случаях при вычислении круговой свёртки прибегают к секционированию?

12. Поясните, в чём принципиальное различие между рядом Фурье и преобразованием Фурье?

13. Каково назначение оконных функций при вычислении спектров сигналов?

14. Укажите достоинства и недостатки двух оконных функций – прямоугольного окна и окна Хэмминга.

15. Из каких соображений выбирают длительность функции времени при оценке её спектра?

16. Что понимают под смещением спектра и почему оно может возникнуть?

17. Каково расстояние по частоте между соседними отсчётами дискретного спектра?

18. Почему в дискретном спектре сигнала столько же отсчётов, сколько и в дискретном представлении исходной функции?

19. Какой временной интервал будет занимать функция времени, полученная из спектра ДПФ?

20. Суть БПФ?

21. Какова связь между непрерывным преобразованием Фурье и её ДПФ?

22. С какой целью применяют дополнение нулями функции?

23. Какие свойства ДПФ позволяют применить БПФ?

24. Чему равно расстояние по частоте между соседними ординатами в спектре ДПФ?

25. Для нахождения ДПФ в математических пакетах ЭВМ имеются встроенные функции для нахождения преобразований Фурье. Пусть дискретная функция времени имеет 80 отсчётов и для неё с использованием встроенных функций находим ДПФ. Затем исходную функцию дополняем нулями до 128 отсчётов и снова находим ДПФ. Сравните полученные ДПФ.

26. Спектр дискретизированной во времени функции занимает весь частотный диапазон. Означает ли это, что низкочастотные и высокочастотные гармонические функции будут представлены в исходной дискретизированной функции?

27. Как от нормированного спектра перейти к естественному?

28. Поясните. ДПФ даёт комплексный спектр?

29. Какие применяют методы нормировки по частоте в ЦОС. ИХ суть.

Чтобы упростить сопоставление частотных характеристик ЦФ с различными _{(шаг дискретизации)}, применяют нормировку частоты. Существует два способа нормировки. При первом способе полагают нормированной частоту ₍частоты ₎, тогда период частотных характеристик равен и требования к ним задаются на интервале . При втором способе используют нормированную частоту . В этом случае период частотных характеристик равен единице и требования к ним задаются на интервале . При этом изменяются аргументы в обозначении частотных характеристик: амплитудно-частотной характеристики, фазочастотной характеристикой, передаточные функции. (₎. Изменяются и сами формулы частотных характеристик.

Выражения для АЧХ и ФЧХ НЦФ при нормированной частоте _:

30. С какой целью применяют преобразование схем ЦФ?

Существует весьма большое число различных форм реализации

рекурсивных и нерекурсивных ЦФ. Рассмотрим наиболее распространенные из них. При построении структурных схем, соответствующих этим формам реализации, будем использовать обозначения операций, широко используемых в теории управления. Операцию задержки (запоминания) отсчетов сигнала на шагов дискретизации обозначим квадратиком с записью в нем величины , операцию сложения нескольких слагаемых ‒ прямоугольником со знаком , а операцию умножения на константу ‒ квадратиком с крестиком внутри. Передачу данных будем отображать на схемах сплошными линиями со стрелками.

Для сравнительного анализа сложности реализации различных форм передаточных функций обычно используют следующие реализационные характеристики:

‒ число ячеек (регистров) оперативной памяти, необходимой для хранения отсчетов входного сигнала и промежуточных результатов;

‒ число ячеек постоянной памяти, необходимой для хранения коэффициентов фильтра;

‒ число умножений, выполняемых при вычислении одного отсчета выходного сигнала;

‒ число алгебраических сложений двух слагаемых, которые должны быть выполнены в фильтре для получения одного отсчета выходного сигнала.

Для рекурсивных фильтров можно выделить четыре основные формы реализации: прямую, каноническую, каскадную (последовательную) и параллельную.

Прямая форма (рис. 8.1) соответствует непосредственной реализации

передаточной функции:

Каноническая форма

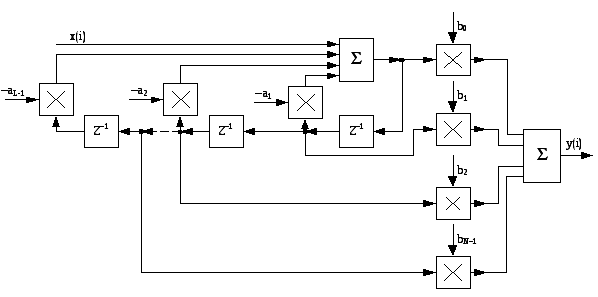
Введение вспомогательной последовательности позволяет объединить часть элементов задержки и уменьшить их число по сравнению с прямой формой реализации. Остальные реализационные характеристики при этом остаются без изменения.

При последовательной форме используется способ представления в виде произведения типовых звеньев не выше второго порядка (биквадратных звеньев)

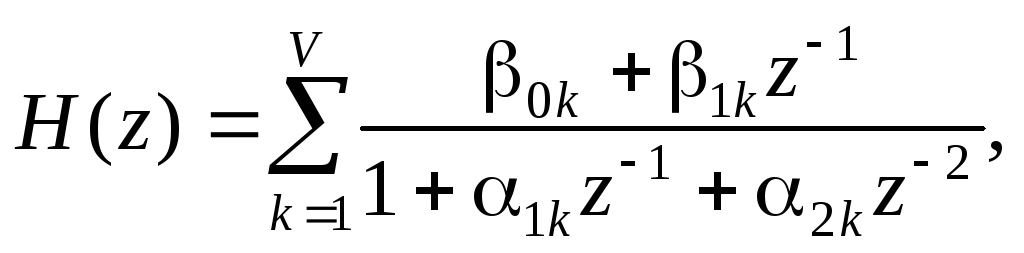
Реализационные характеристики этой формы во многом зависят от числа используемых биквадратных звеньев.

Параллельная форма основана на эквивалентном представлении суммой типовых звеньев, которые могут быть реализованы в виде биквадратного блока при . Реализационные характеристики здесь также сильно зависят от числа типовых блоков.

Все рассмотренные формы реализации РЦФ при одних и тех же входных данных и бесконечной разрядности представления чисел в ЦФ дают абсолютно одинаковые результаты, так как получены путем эквивалентных математических преобразований одного и того же исходного уравнения. Однако при ограниченной разрядной сетке представления чисел, что всегда имеет место в реальных ЦФ, эти формы приведут к различному результату, так как отличаются механизмом преобразования погрешностей округления. Каскадная форма, как правило, обеспечивает наименьший уровень собственных шумов фильтра.

Для нерекурсивных ЦФ возможны прямая и каскадная формы реализации.

Каскадную форму легко получить из каскадной формы РЦФ, если в биквадратных звеньях положить все коэффициенты равными нулю. Для весьма важного типа нерекурсивных фильтров с линейной фазочастотной характеристикой возможны специальные формы реализации, учитывающие свойства симметрии или антисимметрии коэффициентов фильтра . В таких формах реализации число умножений уменьшается практически вдвое. В два раза сокращается и число хранимых в памяти фильтра констант.

31. Покажите зависимость вида АЧХ ЦФ от нулей и полюсов передаточной функции ЦФ.

32. Почему экстремум частотной характеристики цифрового фильтра первого порядка имеется только на нулевой частоте?

33. В каких случаях используют s – преобразование, а в каких z – преобразование?

34. Однозначно ли связаны s и z плоскости?

35. Как осуществляется переход от z –изображения функции к её дискретному представлению?

36. Укажите достоинства представления передаточной функции ЦФ в виде произведения биквадратных блоков.

37. Как определяют порядок ЦФ?

38. Задана передаточная функция ЦФ. Как найти реакцию (выходной сигнал) этого фильтра на входной сигнал x(t)?

39. Как по передаточной функции ЦФ найти его импульсную переходную функцию?

40. ЦФ можно разделить на НЦФ и РЦФ или на БИХ и КИХ фильтры. В чём различие таких разделений?