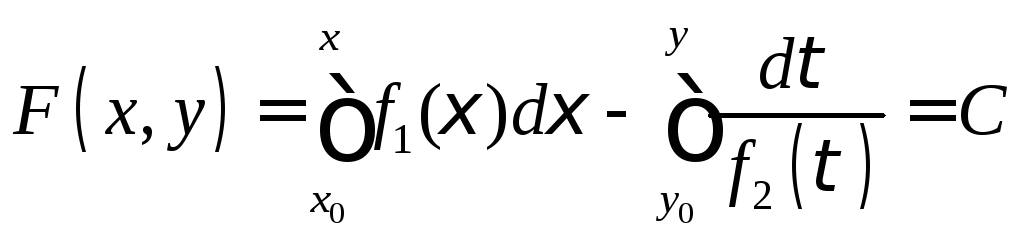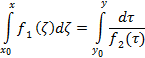Билет № 1

1°. Пример

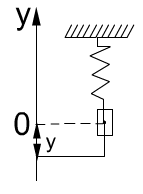, (- ускорение)

(если подобрать )

,

(множество решений)

(положение груза при )

(положение груза в начале колебаний)

2°. Определения.

Опред.: Обыкновенным дифференциальным уравнением -ного порядка называется уравнение, где- независимая переменная,- искомая функция от,- заданная функция отпеременных.

Опред.: Функция называется решением дифференциального уравнения на интервале, если при подстановке в это уравнение она обращает его в тождество по, на интервале.

, - дифференциальное уравнение 1-го порядка.

- решение ДУ интеграл ДУ

Опред.: Интегральная кривая ДУ - график любого решения ДУ.

Опред.: Интегрирование в квадратурах - выражение решения дифференциального уравнения с помощью элементарных функций и интегралов от них.

,

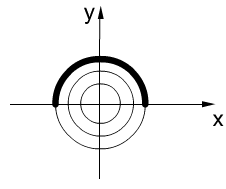(неявная функция, решение ДУ)

Опред.: Интегральная кривая – полуокр. (верхняя или нижняя)

(общий интеграл ДУ)

3°. Геометрический смысл ду.

(это ДУ, разрешенное относительно производной)

- определена в области .

В каждой точке области мы знаем касательную к решению.

Опред.: Совокупность линий называют полем направлений, соответствующим дифференциальному уравнению.

С геометрической точки зрения нахождение решений ДУ- есть нахождение всех кривых, касательные в каждой точке к которым совпадают с соответствующими прямыми поля направлений.

4°. Задача Коши.

Опред.: Задачей Коши для уравнения наз. задача нахождения решенияэтого уравнения, удовлетворяющего условию:,(н. у.).

Билет № 2

1°. Уравнение в полных дифференциалах.

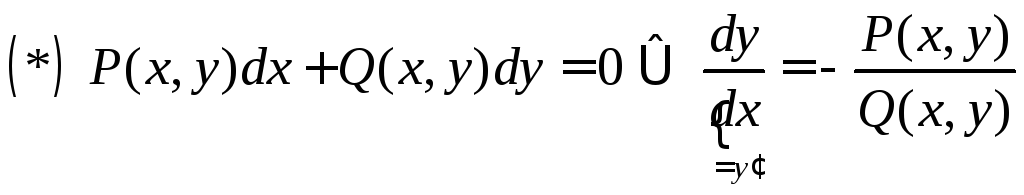
Опред.: Уравнением в полных дифференциалах называется уравнение вида , левая часть которого - полный дифференциал от некоторой функции

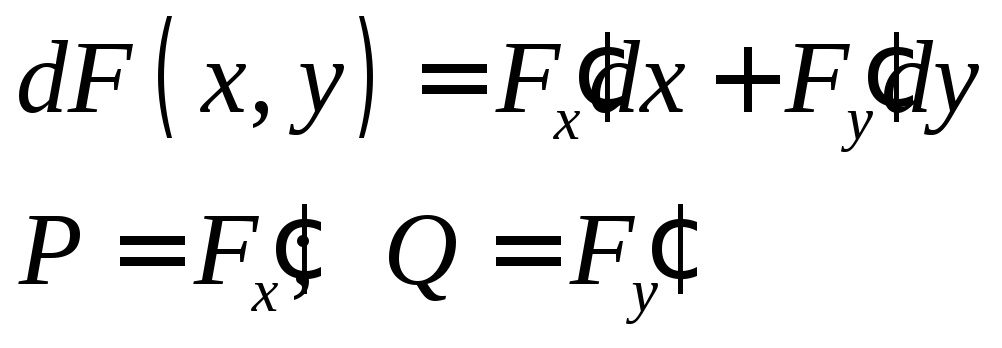
Теорема: Всякое решение уравнения в полных дифференциалах удовлетворяет уравнению для некоторого.

Доказательство: Пусть - решение,- решение

. Теорема доказана.

Теорема:

Пусть функции непрерывны в. Тогда для того, чтобы уравнениебыло уравнением в полных дифференциалах, необходимо и достаточно условие.

Доказательство:

Необходимость.

Достаточность.

,

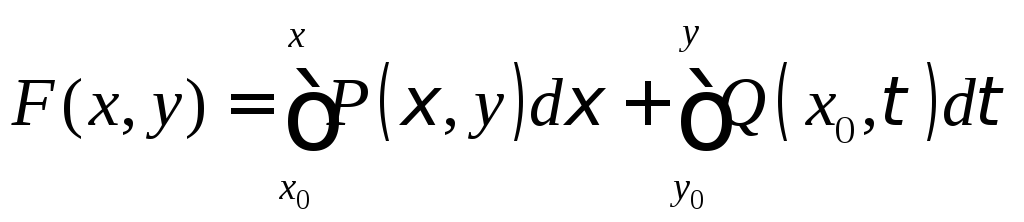
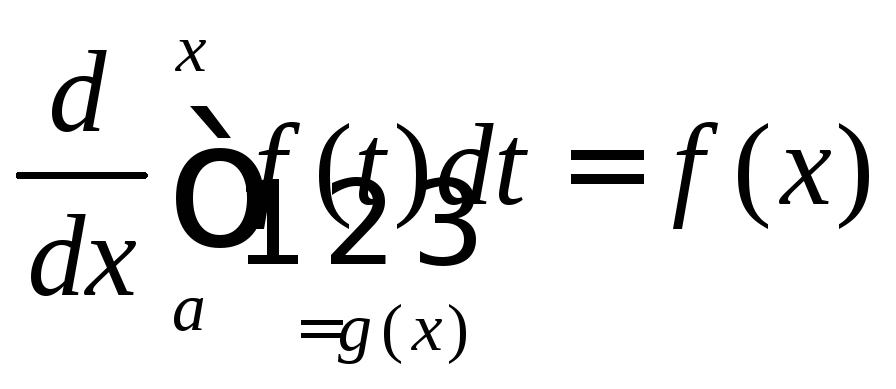
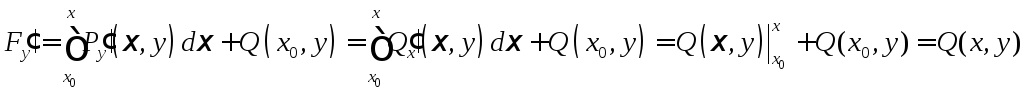
2°. Уравнения с разделяющимися переменными.

Опред.: Уравнение вида , где - непрерывна на,непрерывна на, называется уравнением с разделяющимися переменными.

6°. Интегрирующий множитель.

, ,

Если является уравнением в полных дифференциалах, то называется интегрирующим множителем.

Пример: ,,

Билет № 3

3°. Линейные дифференциальные уравнения 1-го порядка.

Опред.: Если функция , то уравнение называется линейным однородным.

Лемма:

Доказательство:

. .

. -два частных решения.

Метод вариации постоянных.

4°. Уравнение Бернулли.

, где

,

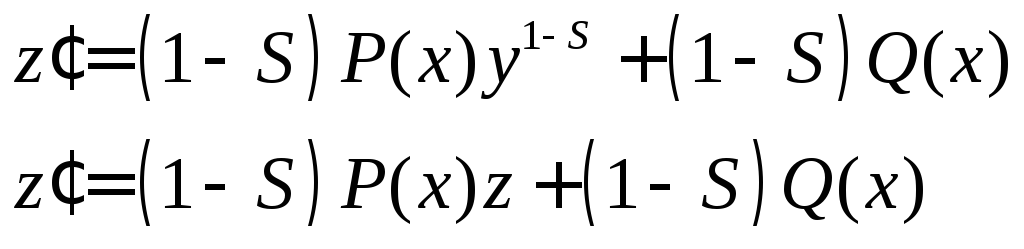
Если , то нужно смотреть, не потеряно ли решение.

5°. «Однородные» уравнения.

Опред.: Дифференциальное уравнение 1-го порядка называется однородным, если его можно привести к виду:

=> =>=>

Билет № 4

1°. Метрическое пространство.

Опред.: Метрическое пространство - это множество , любой паре элементовкоторого поставлено в соответствие неотрицательное число, называемое расстоянием между ними и удовлетворяющее следующим аксиомам:

1.

2.

3.

Пример:

Опред.: называется пределом последовательности, еслипри

Опред.: Последовательность называется фундаментальной, если

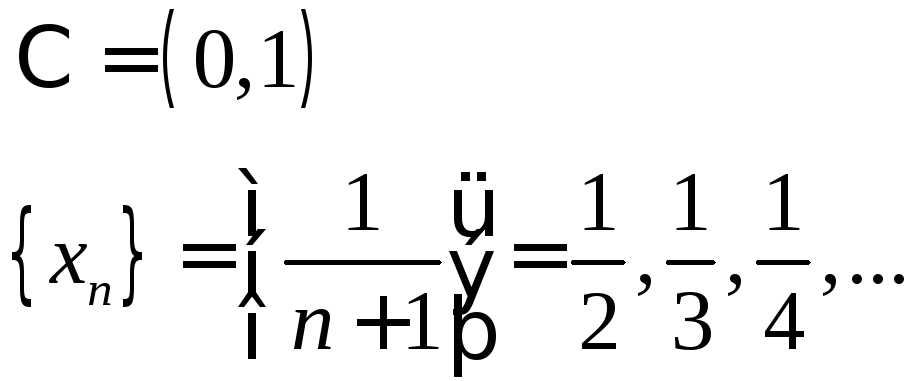
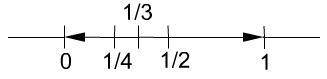
Опред.: Метрическое пространство называется полным, если в нём всякая фундаментальная последовательность сходится к элементу этого же пространства.

Пример:

Теорема:

- полное метрическое пространство

Доказательство:

- фундаментальная последовательность

Фиксируем - числовая, причём справедливо неравенство- фундаментальная

,

- сходится равномерно на

2°. Принцип сжатых отображений.

,

Опред.: Оператор называется сжимающим, если

называется неподвижной точкой оператора , если.

Теорема:

Сжимающий оператор, отображающий полное метрическое пространство в себя, имеет единственную неподвижную точку.

Доказательство:

Докажем единственность.

Докажем существование.

фундаментальная

Билет №5

3°. Теорема о существовании и единственности решения дифференциального уравнения 1-го порядка.

Теорема.

Пусть функция непрерывна в прямоугольнике, причемв. Тогда на интервале, где, существует и единственно решение дифференциального уравнения, удовлетворяющее условию.

Поставленная задача Коши эквивалентна решению интегрального уравнения.

Доказательство.

на .

. ,на,

.

Проинтегрируем это равенство на отрезке :.

Рассмотрим произвольный отрезок :

Рассмотрим метрическое пространство M, состоящее из непрерывных функций на отрезке и удовлетворяющих неравенству:на,M

M.

Рассмотрим произвольную фундаментальную последовательность - худ. изM.

, M

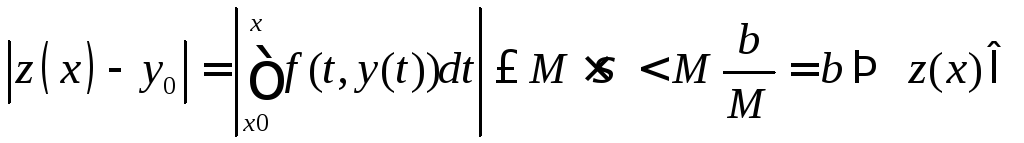Рассмотрим на пространстве M сжимающий оператор : M.

, M

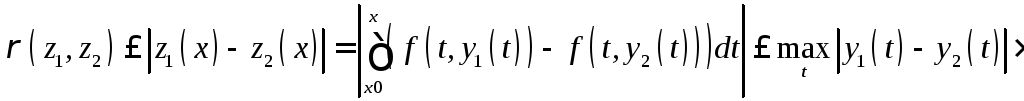
M.

,

M,

Элемент является функцией, удовлетворяющей интегральному уравнению и следовательно исходной задаче Коши.

- непрерывна в

Билет № 6