
PEVM_Chemba_konspekt_lektsy
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
Национальный исследовательский университет «МЭИ»
КОНСПЕКТ ЛЕКЦИЙ по курсу
«Применение ЭВМ в электроэнергетике»
Москва |
2012 |
НИУ «МЭИ» |
1
СОДЕРЖАНИЕ
Лекция №1 Основные задачи расчетов устойчивости режимов ЭЭС и классифика-
ция этих задач………………………………………………………………………….3
Лекция №2 Задачи исследования апериодической статической устойчивости. Цели исследования, математическое описание……………………………………………..8
Лекция №3 Современные алгоритмы проверки статической апериодической ус-
тойчивости.…………………………………………………………………………….12
Лекция №4 Уравнение электромагнитных переходных процессов. Вид характери-
стического определителя……………………………………………………………………………………..….17
Лекция №5 Расчет на ЭВМ статической устойчивости ЭЭС с учетом самораска-
чивания…………………………………………………………………………………………….…..24
Лекция №6 Формирование характеристического определителя……………..29
Лекция №7 Формирование компактной формы записи математической модели ЭЭС…………………………………………………………………………………………………………….32
Лекция №8 Алгоритмические особенности реализации метода D-разбиения……36
Лекция №9 Проверка колебательной устойчивости ЭЭС, заданной всеми параметрами, в том числе и настроечными………………………………………………….39 Лекция №10 Динамические свойства электроэнергетических систем в консерва-
тивной идеализации…………………………………………………………………..43
Лекция №11 Вывод основного уравнения для определения параметров, характеризующих динамические свойства сложных ЭЭС……………………………………56
Лекция №12 Этапы определения показателей, характеризующих динамические свойства сложных ЭЭС…………………………………………………………….61
Лекция №13 Задачи модального анализа динамических свойств ЭЭС. Модальный анализ динамических свойств тестовой системы………………………………...66
Лекция №14 Приведение математической модели ЭЭС к нормальной форме..71
Лекция №15 Полная и частичная проблемы собственных значений. Ме-
тоды их решения…………………………………………………………………...80
Лекция №16 Расчеты динамической устойчивости и длительных переходных процессов. Математические модели основных элементов ЭЭС………………………….....88
Лекция №17 Методы расчета переходных процессов. Решение проблемы жесткости системы дифференциальных уравнений……………………………………....93
Лекция №18 . Особенности организации вычислительного процесса при расчётах динамической устойчивости на ЭВМ……………………………………….……..99
2
Лекция №1
Основные задачи расчетов устойчивости режимов ЭЭС и классификация этих задач
Устойчивость ЭЭС рассматривается на основе методов общей теории устойчивости движения, которая изучает влияние возмущающих факторов на изменение во времени параметров, в частности для ЭЭС – любых режимных параметров: P, U, I, f, S, δ – взаимные углы между осями.
Все возмущающие факторы делятся на
Малые возмущения |
Большие возмущения |
При них математическая модель сис- |
При них математическая модель не |
темы, описывающая ПП в ЭЭС, мо- |
может быть линеаризована, т.е. нель- |
жет быть упрощена заменой нели- |
зя пренебрегать нелинейностью. |
нейностей линейными зависимостями |
Поэтому расчеты переходных про- |
(линеаризация). |
цессов (ПП) приходится проводить |
Это позволяет использовать общие |
для каждой конкретной аварийной |
методы анализа устойчивости линей- |
ситуации и этот класс задач относит- |
ных систем и этот класс задач отно- |
ся к задачам динамической устойчи- |
сится к задачам статической устойчи- |
вости и длительных ПП, когда рас- |
вости, которая в свою очередь, под- |
сматривается большое количество |
разделяется на статическую аперио- |
возмущающих факторов и режимов |
дическую и колебательную устойчи- |
|
вость |
|
Итак, основные задачи расчетов устойчивости:
1. Расчеты и анализ статической устойчивости, в том числе:
а) апериодической устойчивости, т.е. определение предельных по сползанию режимов;
б) колебательной статической устойчивости (по самораскачиванию), куда входит и выбор закона регулирования и настроечных параметров систем автоматического регулирования (САР), в частности, АРВ синхронных машин, а также к колебательной статической относится модальный анализ динамических свойств ЭЭС.
2.Расчеты и анализ динамической устойчивости ЭЭС при различных авариях,
втом числе выбор противоаварийных мероприятий и настройка устройств противоаварийной автоматики (ПА). (Следует заметить, что именно в такой последовательности: апериодическая, колебательная – выбор настроек АРВ и модальный анализ динамических свойств ЭЭС, динамическая устойчивость – Вам предстоит выполнить лабораторные работы).
Остановимся подробнее на задачах расчета статической устойчивости ЭЭС. Статическая устойчивость – способность системы возвращаться в исходное
состояние при малых возмущениях.
3

Согласно статистическим данным ~ 70% случаев нарушения устойчивости ЭЭС происходит именно как нарушение статической устойчивости. Это объясняется тем, что экономически целесообразные пути развития ЭЭС (введение новых генерирующих мощностей, увеличение единичной мощности генераторов, рост номинального напряжения, объединение систем на параллельную работу и т.д.) ухудшают динамические свойства ЭЭС и условия устойчивости систем.
Для того, чтобы оценить статическую устойчивость сложной ЭЭС необходимо, в первую очередь, выяснить, существуют ли ограничения режимов по статической устойчивости, и если да – выявить причины этих ограничений. Тогда уже можно сформулировать рекомендации по обеспечению статической устойчивости с нормативными запасами.
Вспомним немного курс "Электромеханических переходных процессы". Для этого рассмотрим простейшую систему:
Нерегулируемый генератор работает на мощную систему:
Для заданного P0 существует две точки состояния равновесия: устойчивая (т. а) и неустойчивая (т. b). При увеличении P0 эти точки сближаются и сливаются в одну предельную.
Как вы помните из курса "Электромеханические ПП " в этом простейшем случае, когда учитывается только уравнение движения нерегулируемого генератора, характеристическое уравнение имеет вид:
4

p2 Pd p ном С1 0 , а корни этого уравнения
TJ TJ
p1,2 |
|
|
Pd |
|
|
|
Pd |
2 |
|
ном |
C1 |
|
|
|
|
|
|
|
|
||||||||
|
TJ |
|
|
|
|
|
|||||||
|
2 |
|
|
|
2 TJ |
|
TJ |
|
|
||||
На восходящей (устойчивой) |
части угловой характеристики C |
dP |
0 , а |
||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ПП при малом возмущении имеет периодический характер ( и под корнем "-
", т.е. j |
|
|
|
|
возрастающим периодом колебаний T ( f |
|
1 |
|
||||||||
|
... ) с |
частота |
||||||||||||||
|
T |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уменьшается с увеличение угла δ). |
|
|
|
|||||||||||||
При значении угла δ1 |
< δ < δ |
max, что |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Pd |
|
|
|
Pd |
2 |
|
|
|
|||||||
|
|
|
|
|
|
ном |
C1 , решение определяется корнями |
p1,2 |
, |
|||||||
|
|
|
|
|
||||||||||||
|
2 TJ |
|
2 TJ |
|
TJ |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
e t и e t , где , т.е. при приближении к δmax – затухающий апериодический процесс, определяемый двумя действительными отрицательными корнями.
|
В точке характеристики P = f(δ), когда δ = δmax, а |
dP |
0 режим, предельный |
||||||||
|
|
||||||||||
|
|
|
|
|
|
|
|
d |
|
|
|
по |
мощности, |
является |
предельным и по устойчивости, т.к. при C |
dP |
0 |
||||||
|
|||||||||||
|
|
|
|
|
|
|
1 |
d |
|||
|
|
|
|
|
|
|
|
|
|
||
p1,2 |
|
|
Pd |
|
Pd |
– один корень p1= 0, а другой p2= -α это точка δmax – точка не- |
|||||
|
TJ |
2 TJ |
|||||||||
|
2 |
|
|
|
|
|
|
|
|||
устойчивого равновесия – сползание. |
|
|
|||||||||
|
При δ > δmax С1<0 и |
p1,2 , где , т.е. из двух вещественных кор- |
|||||||||
ней характеристического уравнения один p1>0, а другой p2<0, т.е. система неустойчива и процесс носит апериодический характер. Запас по мощности и по ус-
тойчивости в данном случае совпадают, и k P в общем случае определяется нор- |
|||
|
|
з |
|
мированной величиной |
|
|
|
|
k P |
Pmax P0 |
100% |
|
|
||
|
з |
Pmax |
|
|
|
|
|
k P 20% – для нормальных режимов; |
|
||
з |
|
|
|
k P 8% |
– для послеаварийных режимов. |
|
|
з |
|
|
|
Следует подчеркнуть, что предел мощности (т.е. предел по существованию режима) и предел апериодической статической устойчивости не всегда совпадает. Уже в схеме "станция-станция" для нерегулируемой системы, предел мощности и устойчивости не совпадают, и предел мощности оказывается устойчивым.
5
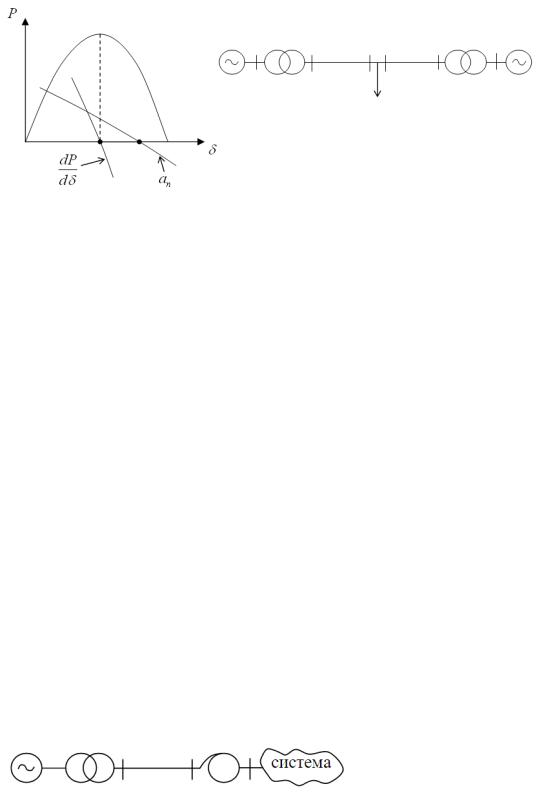
Как только для этого нерегулируемого генератора помимо уравнения движения ротора мы учтем уравнение электромагнитных переходных процессов в обмотке возбуждения, так рассмотрение тех же, только необходимых условий устойчивости (положительность коэффициентов характеристического уравнения) вскрывает еще один вид нарушения статической устойчивости – самовозбуждение, которое появляется за счет емкостного характера внешнего сопротивления. В данном случае, способ борьбы с этим видом нарушения статической устойчивости – включение реактора, ограничение степени продольной компенсации или увеличение числа генераторов, работающих на станции в режимах синхронизации.
Если для этого же случая рассмотреть еще и достаточные условия устойчивости, то проявится еще один вид нарушения статической устойчивости: параметрическое самораскачивание, которое проявляется в режимах, близких к холостому ходу (δ < α), т.е. отсутствие демпфирования, а в режимах передачи малых мощностей P область его проявления зависит от соотношения параметров схемы замещения. Способы борьбы с этим видом нарушения статической устойчивости – появление у современных генераторов заметного демпфирования и малых r.
Сказанное показывает даже на простейшем примере нерегулируемого генератора разнообразие причин нарушения статической устойчивости и способов ее обеспечения. Это обстоятельство не позволяет решать эту задачу каким-либо одним методом.
Именно эту мысль могут подтвердить два примера из опыта эксплуатации: Пример 1: В свое время были сооружены АЭС с агрегатами по 220 МВт в
ГДР (АЭС Hopg) и в Болгарии (АЭС Козлодуй) (теперь их закрыли). Генераторы на них имели АРВПД с высокочастотной системой возбуждения.
В обоих случаях оказалось, что при увеличении P до Pном возникали низкочастотные (f < 1Гц) колебания тока и мощности, препятствующие нормальной работе АЭС. Исследования (проводившиеся на нашей кафедре) показали, что причина – чрезмерно большое значение коэффициента усиления по отклонению на-
6

пряжения kou. Снижение kou до значений, обеспечивающих приемлемую точность поддержания напряжения на зажимах генераторов, привело к исчезновению этих колебаний, т.е. к стабилизации ЭЭС (способ обеспечения устойчивости).
Пример 2 При объединении на параллельную работу двух ЭЭС (Италия и бывшая
Югославия) возникали низкочастотные колебания тока и мощности по межсис-
темной связи даже в условиях Pперет = 0 (нулевой переток по этой ВЛ). Исследования показали, что для стабилизации режимов данного энергообъединения необхо-
димо ввести более эффективную (быстродействующую) систему возбуждения на одной из станции и более эффективные АРВСД.
Таким образом, мы видим, что в одном случае способ обеспечения устойчи-
вости при P ≈ Pном < Pmax состоит в улуч-
шении стабилизирующих свойств АРВ за счет снижения kou, в другом случае при P0 << Pmax для обеспечения устойчивости потребовалось перейти от АРВПД к АРВСД с быстродействующей системой возбуждения.
А в случаях, когда Pном > Pmax никакими АРВ обеспечить устойчивость нельзя, т.к. это свидетельство того, что пропускная способность ВЛ – недостаточна и
для обеспечения нормативного kзP эту ВЛ нужно усилить.
Все сказанное лишний раз подтверждает, что из-за разнообразия причин нарушения статической устойчивости решать задачу обеспечения устойчивости ка- ким-либо единым методом нельзя и в связи с этим общую задачу исследования статической устойчивости ЭЭС разделяют на несколько подзадач.
Классификация задач расчета статической устойчивости ЭЭС
В первую очередь разделяют устойчивость электромагнитных (самовозбуждение) и электромеханических 0переходных процессов в ЭЭС.
Статическая устойчивость
Электромагнитные ПП |
|
Электромеханические ПП |
|
|||
|
|
|
|
|||
|
Апериодическая стати- |
|
Колебательная |
|||
|
ческая устойчивость |
|
статическая ус- |
|||
|
|
|
|
|
тойчивость |
|
7

Электромагнитные ПП выявляются при достаточно детальном математическом описании электромагнитных ПП, которые учитывают в генераторах, ВЛ, трансформаторах и т.д. Когда исследуют электромагнитные ПП механические ПП, обусловленные изменением скорости вращения роторов машин не учитываются, т.к. считается, что процесс электромагнитной неустойчивости развивается столь быстро, что инерционные механические координаты не успевают скольлибо заметно измениться.
Таким образом, в данном курсе предмет рассмотрения – статическая устойчивость электромеханических (т.е. взаимосвязанных механических и электромагнитных ПП). Эти процессы относительно медленны – частоты колебаний лежат в диапазоне 0< f <5Гц. При этих частотах электромагнитные процессы в элементах сети и статорных цепях можно не учитывать.
Таким образом, в итоге, задачи исследования статической устойчивости в данном курсе делим на две большие группы, которые различаются целью исследования, математическим описанием и методами решения и анализа.
Лекция №2
Задачи исследования апериодической статической устойчивости. Цели исследования, математическое описание.
Итак, при исследовании апериодической статической устойчивости предполагается, что все САР выбраны так, что самораскачивание в системе исключено, и нарушение устойчивости может носить только апериодический характер. Математически это означает, что один действительный корень переходит из левой полуплоскости в правую.
Основная причина сползания – недостаточная пропускная способность сети. Цель исследования – определение области апериодически устойчивых режи-
мов для определения минимальных значений kзP .
Математическое описание ЭЭС определяется только статическими характеристиками.
Метод исследования сводится к проверке необходимого условия устойчивости – оценке знака свободного члена характеристического уравнения an .
Пути расширения области апериодически устойчивых режимов:
8

а) на уровне эксплуатации – введение оперативных ограничений на перетоки мощности в различных сечениях ЭЭС;
б) на уровне проектирования – увеличение пропускной способности сети:
-сооружение дополнительных линий или цепей, повышение класса напряжения;
-применение УПК;
-установка регулируемых ИРМ,
-применение управляемых линий переменного тока (гибких линий), объединенных аббревиатурой FACTS – на основе преобразо-
вательной техники (Flexible (гибкий) Alternating (переменный) Current (ток)
Transmission (передача) System (система)).
2-я группа – задачи исследования статической ЭЭС с учетом самораскачивания.
Самораскачивание – это колебание режимных параметров с возрастающей амплитудой.
T - период [с]
p1,2 j |
f |
1 |
Гц |
2 f |
|
2 |
рад/с |
T |
|
||||||
|
|
|
|
|
T |
||
Математически такое нарушение устойчивости означает переход пары комплексно сопряженных корней из левой полуплоскости в правую. Пересечение мнимой оси – система на границе устойчивости.
Причина нарушения устойчивости – неправильный выбор структуры или настроечных параметров каналов (систем) стабилизации САР, в первую очередь
АРВСД генераторов. Для АРВСД выбраны настройки kof* и k1*f (режим "а").
При утяжелении режима область обычно смещается вверх и в сторону и для режима "b" настройка kof* , k1*f находится вне зоны устойчивости режима "b". При
ней в режиме "b" начнется самораскачивание, т.е. в том случае, если настройка лежит вне зоны устойчивости, то происходит самораскачивание.
Цель исследования: выбор таких структур и настроечных параметров систем стабилизации АРВ, САР ИРМ, ВПТ, которые обеспечивают требуемые условия статической устойчивости внутри области апериодической статической устойчивости.
9
Математическое описание ЭЭС состоит из линеаризованных дифференциальных уравнений ПП (электромеханических и электромагнитных в контурах ротора генератора, включая систему возбуждения и АРВ) и алгебраических уравнений, связывающих параметры режима электрической сети.
Методы исследования:
1)частотные методы для определения областей колебательной устойчивости в плоскости настроечных параметров САР (метод D-разбиения), критерий Михайлова;
2)методы линейной алгебры для модального анализа динамических свойств системы по собственным значениям (СЗ) и собственным векторам (СВ) матрицы состояния системы.
Пути улучшения колебательной статической устойчивости:
1)выбор оптимальных структур и каналов стабилизации систем автоматического регулирования (выбор настроечных параметров систем стабилизации (САР
иАРВСД));
2)выбор оптимального закона управления САР (что характерно для новых систем).
Определение предельных режимов ЭЭС по условиям апериодической статической устойчивости (критерий апериодической статической устойчивости, понятие пре-
дельного режима)
Итак, мы вспомнили, что выполнение необходимого условия статической устойчивости (положительность всех коэффициентов характеристического уравнения D( p) 0 , т.е. ai 0, i 1,..., n при a0 0 ) гарантирует отсутствие в правой по-
луплоскости действительных корней. Это значит, что an , характеризующий пере-
ход действительного корня в правую полуплоскость – положителен, т.е. an 0 (т.е. самораскачивание отсутствует).
Мы не зря подчеркиваем, что первый этап исследования статической устойчивости – это исследование апериодической статической устойчивости, т.е. в этом случае мы считаем, что САР настроены так, что самораскачивание в системе отсутствует. Действительно, если характеристической уравнение системы имеет порядок "n" и имеет вид
D( p) a |
pn a pn 1 |
a pn 2 |
... a |
p a |
0 |
(1) |
0 |
1 |
2 |
n 1 |
n |
|
|
или будучи разложенным на множители: |
|
|
|
|
||
D( p) a0 ( p p1) ( p p2 )....( p pn 1) ( p pn ) 0 |
(2) |
|||||
(имеем "n" корней; pi – корни характеристического уравнения для устойчи-
вой системы должны иметь отрицательные вещественные части) Для того, чтобы найти аналитическое выражение для свободного члена характеристического уравнения полагаем в (1) и (2) p 0
Тогда D(0) an
D(0) ( 1)n a0 p1 p2...pn 1 pn и приравняв правые части получаем
10
