3.3. Типовой пример определения параметров нелинейности и выбора оптимального режима

Пусть требуется аппроксимировать полиномом седьмой степени экспериментальную зависимость коэффициента усиления усилителя на ПТ2П907А(3J) и на основе вычисленных коэффициентов аппроксимации и гармонического анализа с использованием метода МКП по формулам (2-6) определить параметры нелинейности и выбрать оптимальный режим транзистора.

Аппроксимацию проводим в следующей последовательности.

1. Задаем 11 экспериментальных значений коэффициента усиления в равноотстоящих точках напряжения смещения «затвор-исток» в интервале В. Эти данные, а также вспомогательные значения нечетных 2К_н и четных 2К_ч компонент коэффициента усиления в симметричных точках смещения U_зи сводим в табл. 2.

2. U_{зин =} U_{зи +} 1,5

Таблица 2

х	-1,0	-0,8	-0,6	-0,4	-0,2	0	0,2	0,4	0,6	0,8	1,0
Uзи	-1,5	-1,2	-0,9	-0,6	-0,3	0	0,3	0,6	0,9	1,2	1,5
Кэ	4,0	4,2	4,62	5,6	8,35	42,0	56,5	71,0	85,2	99,5	113
2Кн	-	-	-	-	-	0,00	48,15	65,40	80,58	95,30	109,0
2Кч	-	-	-	-	-	84,00	64,85	76,60	89,82	103,7	117,0
В0	3,961451	4,12365	4,60254	5,51678	8,29526	52,097022	56,2355	70,6987	85,0241	98,1852	113,0
Uзин	0	0,4	0,8	1,2	1,6	2,0	2,4	2,8	3,2	3,6	4,0

2. Находим коэффициенты разложения ортогональных полиномов по формулам (25) преобразовав их при N=11 в выражения (26)

(26)

Заметим, что при определении коэффициента D₀ используется вторая формула (25), а из табл. 1 следует, что при N=11 нулевой полином для любого х имеет величину , поэтому в соответствии с формулой (22) можно найти сумму всех значенийтабл. 2, и поделить на 11, т.е.

.

Для определения используем первую формулу (26). Входящие в нее нечетные компонентыберем из табл. 2 (это разностные значенияв симметричных точках), а значения полинома– из табл. 1

Для определения используем вторую формулу (26), в которой четные компонентыявляются суммарными значениямив симметричных точках аргументах, кроме точки х=0, в которой значение .

Аналогично находим остальные коэффициенты:

; ;;

; ;;

; .

Полином по степеням х находится по формуле (19), с преобразованием ее в (27), в которой аппроксимирующий полином в отличие от аппроксимируемой функции обозначен как:

, (27)

где – ортогональные полиномы.

Группируя коэффициенты по степеням х и собирая подобные члены, приходим к удобным выражениям для вычисления членов А₀, А₁х, А₂х², А₃х³ и т.д. этого полинома:

;

;

;

;

;

;

;

.

В итоге полином по степеням х:

; (28)

Для перевода этого полинома в истинный полином по степеням необходимо уточнить, удовлетворяют ли значенияусловиям трех нижеследующих формул:

- при совпадении значений их

= 0 и х = 0 (29)

- при несовпадении значений их

при = 0 …, (30)

при (31)

Рассматриваемый полином удовлетворяет требованиям формулы (30). Подставляем в (28) значение

,

получаем истинный полином по степеням :

(32)

По найденному уравнению вычисляем и заносим в нижнюю графу табл. 2 значения В₀ в контрольных точках напряжения смещения .

Из сопоставления экспериментальных значений и теоретических В₀ рис. 4 видим, что совпадение очень хорошее. Абсолютная ошибка находится в пределах сотых долей, что характеризует пригодность результатов аппроксимации для дальнейшего гармонического анализа различных нелинейных явлений. В заключение отметим, что с помощью простых современных микрокалькуляторов без привлечения компьютерных программ такую аппроксимацию можно выполнить за 10-15 минут.

Полученные коэффициенты аппроксимации используем для определения параметров нелинейности и коэффициентов интермодуляционных искаженийв широком диапазоне смещений , что позволит выбрать по этому виду нелинейностиоптимальный режим, при котором стремится к нулю, а коэффициент усиления В₀ максимально возможный. Заметим, что экспериментальные определения коэффициентов и параметров нелинейности на основе ранее описанного двухсигнального метода связано с громоздкими измерениями. При этом определение оптимального режима становится вовсе проблематичным [11, 12].

Рис. 4. Экспериментальная (пунктиром) и теоретическаякривые

(аппроксимирующий полином) и полученная зависимость

в функции от напряжения затвора усилителя на ПТ 2П907А(3J).

Для определения найдем первую и вторую производные полинома, значение которых целесообразно занести в табл. 3, совмещая их с данными самого полинома в тех же контрольных точках.

(33)

Тогда с учетом коэффициентов найденного полинома (32) имеем

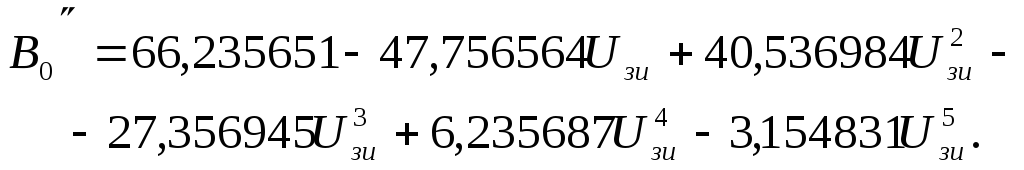(34)

Далее по формуле (11) вычисляем , который заносим в табл. 3 и по ее данным строим совмещенные зависимостиив функции от напряженияи определяем оптимальный режим, при котором параметримеет минимальное значение при максимально возможном коэффициенте усиления(рис. 4).

Таблица 3

, В	-1,5	-1,2	-0,9	-0,6	-0,3	0	0,3	0,6	0,9	1,2	1,5
Uзин	0	0,4	0,8	1,2	1,6	2,0	2,4	2,8	3,2	3,6	4,0
	3,961451	4,12365	4,60254	5,51678	8,29526	52,097022	56,2355	70,6987	85,0241	98,1852	113,0
	-	32,8923	20,812	15,9125	7,895	5,321	-6,825	-4,365	-2,214	- 0,962	-2,754
, 1/В2	-	3,988	2,26	1,442	0,475	0,064	-0,06	-0,0309	-0,01	-0,0049	-0,013

По данным табл. 3 и графикам рис. 4 легко определить, что оптимальный режим составляет ≈1,2 В, при этом имеет место максимальное ослабление комбинационных составляющих 3-го порядка с амплитудамии частотамии.

Коэффициент интермодуляционных составляющих , соответствующий этому ослаблению, согласно формулы (4) при амплитуде бигармонического интермодулирующего сигнала на выходеВ (рис. 3) равен:

=0,25··0,14²=0,0000241 раз

или в дБ: (дБ) = 20lq k₃ = 20lq0,0000241 ≈ 92 дБ.

При этом амплитуды бигармонической комбинационной (интермодуляционной) составляющей с упомянутыми частотамииравны

= 0,0000241·0,14·10≈3,4мкВ.