коллок

Тема 1. Введение. Первичные понятия теории вероятностей и простейшие способы определения вероятности.

Экскурс в историю развития теории вероятностей. Случайные явления и предмет теории вероятностей. Основные типы задач, решаемых с применением вероятностно-статистических методов и моделей. Понятия случайного эксперимента (испытания) и события. Случайное, невозможное и достоверное события. Статистическая устойчивость частот событий и интуитивное представление о вероятности. Пространство элементарных событий с конечным числом исходов и классическое определение вероятности. Геометрический и статистический способы определения вероятностей.

Вспомогательные сведения.

Предмет – то, на что направлена мысль, и что составляет ее содержание. Цель – то, к чему стремятся, что хотят осуществить.

Явление – всякое проявление чего-нибудь, как-нибудь.

Предмет теории вероятностей. Теория вероятностей – математическая наука, изучающая математические модели случайных явлений.

Случайное явление – протекающее спонтанно или воспроизводимое в ходе эксперимента явление, исход которого не предопределен в рамках его наблюдения (или постановки эксперимента). Должно обладать свойством статистической устойчивости событий, связанных с данным явлением.

Прикладные задачи теории вероятностей и математической статистики

1.Статистический приемочный контроль.

2.Оценка надежности системы.

3.Актуарные и финансовые расчеты.

4.Анализ СМО (систем массового обслуживания).

5.Прогнозирование временных рядов.

6.Маркетинговые исследования.

7.Изучение предпочтений, опросов общественного мнения. Например, Фехнер (1860, психофизика) сравнивал мало отличимые веса сосудов (300-3000 г 0,04-0,08).

8.Исследование взаимосвязей показателей и динамики стохастических процессов.

9.Воздействие средств массовой информации, размещение рекламы.

10.Анализ причин и характера безработицы

11.Управление запасами.

12.Выбор места отдыха (условия проживания, возможные развлечения, расходы, погода).

13.Другие.

Краткий исторический экскурс в становление теории вероятностей и математической статистики как научных дисциплин.

Первый период. Теория вероятностей возникла в середине 17-го века. Первые работы (Б. Паскаль, П. Ферма и Х. Гюйгенс) связаны с подсчетом шансов в азартных играх и делением ставки в случае преждевременного окончания игры. Я. Бернулли (1713) установил ЗБЧ для схемы независимых испытаний с двумя исходами.

Классическая задача Де Мере (1654 г., Де Мере написал Паскалю)

1660 г. (Англия) Дж. Гранти, У. Пети подготовили социально-статистические обзоры по численности смерти и образе жизни.

Второй период (18-й век – середина 19-го). Связан с работами таких ученых как А. Муавр, П. Лаплас, К. Гаусс и С. Пуассон. Результаты нашли применение в теории ошибок наблюдений (геодезия, астрономия, теория стрельбы). Основные научные достижения: теоремы Лапласа и Пуассона, МНК (метод наименьших квадратов).

Появилась анкета. Д. Девис (1787) изучал семейные бюджеты. М. Иден (1794) подготовил отчет о положении бедных.

Третий период (2-я половина 19-го века). Исследования в России занимают ведущее место в мире. Российские ученые: П. Л. Чебышев, А. М. Ляпунов, А. А. Марков. Достижения: ЗБЧ и ЦПТ, цепи Маркова (случай зависимых испытаний).

В Западной Европе во 2-й половине 19-го века получили развитие работы по математической статистике: Бельгия – А. Кетле (ввел среднее, как один из индикаторов, доступных количественному анализу), Англия - Ф. Гальтон (регрессия), Австрия – Л. Больцман (статистическая физика). Выборочный метод впервые применил Артур Боули в 1912 к анализу данных опросов.

Четвертый период (современный). Теория вероятностей и математическая статистика приобретают современные теоретические основы. Ученые: Э. Борель, П. Леви, М. Фреше (Франция); Р. Мизес (Германия); Н. Винер, В. Феллер, Дж. Дуб (США); Г. Крамер (Швеция); С. Н. Бернштейн (предельные теоремы), А. Я. Хинчин, А. Н. Колмогоров, Е. Е. Слуцкий (развитие теории случайных процессов), В. И. Романовский, Н. В. Смирнов, Ю. В. Линник, Л. Н. Большев (МС), и многие другие.

1934 – Д.Гэллап создал Американский институт общественного мнения.

Первичные понятия ТВ.

Осуществление некоторого комплекса условий – испытание (эксперимент, опыт,

наблюдение).

Определенный результат испытания – событие («наивное» определение, строгое – позже). Определяется обычно посредством высказывания.

Выделяют три типа событий: случайное (обозначение: A, B, C, ), достоверное ( ) и

невозможное ( ).

Случайное событие – любая комбинация исходов испытания, имеющая определенную вероятность наступления.

Вероятность – числовая характеристика возможности осуществления случайного события. Если результат испытания – число или конечный набор чисел, то его исходы описывают с

помощью случайной величины (СВ). Если исходы опыта представляют собой последовательности, функции, кривые, преобразования, то для описания исходов используют понятие случайный элемент (функция, процесс и т.д.).

Случайный элемент – обобщение понятия СВ. Термин, видимо, введен М. Фреше (1948), посчитавшим, что развитие ТВ и расширение области ее приложений привело к необходимости от схем, где случайные исходы опыта могут быть описаны числом или конечным набором чисел, к схемам, где исходы опыта представляют собой, напр., функции, кривые, преобразования.

ТВ позволяет по вероятностям одних случайных событий находить вероятности других случайных событий, связанных каким-либо образом с первыми. Такие расчеты основаны на том, что массовые случайные явления в стационарных условиях обладают свойством статистической устойчивости частот событий. Свойство проявляется в затухании с ростом количества наблюдений колебаний относительной частоты события относительно некоторого числа, называемого вероятностью этого события.

Элементарное событие – элементарный (наиболее простой) исход случайного эксперимента. Эксперимент заканчивается одним и только одним элементарным исходом. Эти исходы неразложимы и взаимно исключают друг друга. Могут иметь различную природу: число, вектор, кривая, качественная характеристика.

Несовместные события – не могут произойти одновременно в одном и том же испытании. Пространство элементарных событий – множество всех элементарных исходов

испытания. Невозможное событие трактуется как пустое множество, случайное событие – как некоторое подмножество . Наиболее общие абстрактные результаты в ТВ получены в предположении, что пространство имеет произвольную математическую природу. Более конкретные и доступные для понимания результаты получены в предположении, что имеет определенную математическую природу: является дискретным множеством, множеством или подмножеством k .

Решение. Испытание – бросание трех монет Исход – последовательность из трех монет

A выпадет 3 раза одна и та же сторона

n 2 2 2 8 m 2

Пример 2. В урне 9 шаров: 2 белых, 3 черных, 4 синих. Из нее случайным образом извлекаются 3. Найти вероятности следующих событий: A = {все извлеченные шары белые}, B ={все извлеченные шары синие}, С = {одного цвета}, D = {среди извлеченных хотя бы 2 черных шара}, E = {все шары разного цвета}.

Решение. Испытание – извлечение трех шаров. Исход – три определенных шара,

n С93 9 8 7 ,

3!

Пример 3. Составляется список из 5 фамилий. Сколькими способами это можно сделать, если 1) все фамилии различные, 2) имеются 3 одинаковые фамилии?

Решение. Испытание – составление списка. Исход – список.

A список из 5 различных фамилий ,

В список из 5 фамилий, среди которых две одинаковых ,

C список из 5 различных фамилий, чтобы две определенных фамилии стояли рядом ,

Пример 4 (задача о сравнении двух выборок). Планируется проведение двух серий измерения роста X : X1, , X n1 – возможные результаты измерений роста юношей, Y1, ,Yn2 – возможные

результаты измерений роста девушек. При проверке гипотезы однородности данных по критерию Манна-Уитни исходные данные объединяют и упорядочивают в порядке возрастания. Какова вероятность событий:

Пример 5 (семейная задача). В семье 4 сестры по очереди моют посуду. Из 4-х разбитых тарелок 3 разбито младшей сестрой. Можно ли ее оправдать, приписывая эти неудачи случайности. Решение. Вероятность случившегося события в предположении о равной вероятности разбития

Вывод: происшедшее нельзя объяснить неблагоприятным стечением обстоятельств.

Статистическое определение вероятности.

Вероятность случайного события полагается равной его относительной частоте, вычисляемой по результатам n независимых повторных испытаний:

m( A)

Wn ( A) n P( A) .

Здесь m A – частота A (число появлений события A), а m A 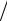n – его относительная частота

(частость).

Дж. Граунт (1620-1675): относительная частота смерти детей в возрасте от 0 до 6 лет равна

71124/229250 = 1/3.

Геометрическое определение вероятности.

Множеству элементарных исходов испытания поставим в соответствие некоторую геометрическую область G, а случайному событию A – геометрическую область GA . Тогда, если все исходы испытания равновозможны, вероятность появления события A можно найти по

формуле геометрической вероятности: P( A) мера(GA ) . В качестве меры используется длина,

мера(G)

площадь, объем в зависимости от вида геометрической области.

Пример (задача о встрече). Два судна должны прибыть в порт назначения от 13 до 14 часов. в порту один причал для разгрузки. Продолжительности разгрузки судов 5 мин. и 10 мин. Найти вероятность того, что одному из них придется ожидать окончания разгрузки другого?

Решение. В данном случае:

испытание – прибытие двух судов,

Им соответствует изображение

Поэтому

Тема 2. Аксиоматическое построение теории вероятностей

Операции над событиями: пересечение, объединение, дополнение, разность, импликация. Основные свойства операций над событиями. Алгебра и -алгебра событий, событие как измеримое (наблюдаемое) множество. Аксиоматическое определение вероятности А.Н. Колмогорова. Вероятностное пространство, примеры вероятностных пространств. Следствия из аксиом: непрерывность вероятностной меры, свойства вероятности для объединения несовместных и совместныхсобытий, а также для объединения событий,образующихполную группу.

Действия над событиями и их геометрическая интерпретация. Свойства операций.

1.Пересечение (произведение) событий – событие, состоящее в их совместном появлении:

A B A B AB .

2.Объединение событий – событие, состоящее в появлении одного из них: A B. Сумма событий – объединение несовместных событий: A B.

4.Дополнение событий: A \ A. A – событие, противоположное к A.

5.Импликация событий: A B.

6.Равносильность событий: A B A B B A .

Примеры применения операций над событиями: сдача экзамена в «жестком» режиме,

освещение помещения люстрой, получил «3» – сдал экзамен.

Замечание. Возможна геометрическая интерпретаций операций над событиями с помощью диаграмм Эйлера-Венна, если испытанию поставить в соответствие бросание точки в прямоугольник, а каждомусобытию – круг в прямоугольнике.

Свойства операций над событиями.

1. Ассоциативность и коммутативность операций , – результат выполнения операций

Примеры содержательной интерпретации операций над событиями.

Пример 1. Пусть Ai = {i-й квартал фирма завершит с прибылью}, i 1,2,34. Тогда

4 Ai – весь год с прибылью,

i 1

2 Ai – первое полугодие с прибылью,

i 1

A1 A2 A3 A4 – только первый квартал с прибылью,

4

Ak Ai – только один квартал с прибылью,

4 Ai – по крайней мере (хотя бы) один квартал с прибылью.

i 1

Пример 2. Пусть – прибыль за год (в у.е.). Тогда

10 10 ,

5 10 ,

Случайное событие и вероятностное пространство (аксиоматический подход).

Аксиоматический подход тесно связывает ТВ с современной теорией функций и теорией множеств.

Основная проблема. Если более чем счетно, то определяя событие как его подмножество, невозможно построить логически непротиворечивую теорию. Причина кроется в существовании неизмеримых множеств.

Решение проблемы. Выделяется определенный класс подмножеств, элементы которого и объявляются событиями.

Вспомогательные сведения.

Множество измеримо, если его можно «сколь угодно точно приблизить» элементарными множествами. На прямой – отрезками, в пространстве – параллелепипедами и т.д.

Пример неизмеримого множества (Колмогоров, Фомин). C – окружность длины 1, - иррациональное число. К одному классу отнесем те точки окружности, которые могут быть переведены одна в другую поворотом окружности на угол n ,n Z. Из каждого класса берем по одной точке. Полученное множество неизмеримо.

Алгебра множеств – непустая система подмножеств A из :

1)A,

2)A A A A,

3)A,B A A B A.

-алгебра множеств (система подмножеств, замкнутая относительно счетного числа теоретикомножественных операций)– непустая система подмножеств A из :

1)A,

2)A A A A,

3*) A1,A2, A A1 A2 A.

Задать топологическое пространство – задать некоторое множество X и указать те подмножества, которые считаются открытыми.

Пару ,A называют измеримое пространство.

Пример (борелевская -алгебра). Борелевская -алгебра – наименьшая -алгебра подмножеств топологического пространства, содержащая все его открытые подмножества. Ее элементы называются борелевскими множествами. На числовой прямой R борелевская -алгебра задается на интервалах, в многомерном пространстве – на параллелепипедах.

Примечание.

Далее – пространство элементарных событий, а A – -алгебра множеств, заданная на этом пространстве. Все элементы из A называются событиями, все остальные элементы событиями не являются.

Испытание (trial) при аксиоматическом подходе – любое разбиение пространства элементарных событий на попарно непересекающиеся события, которые называются «исходами испытания».

Аксиоматическое определение вероятности (Колмогоров А.Н.)

Вероятность на ,A есть числовая функция, определенная на множествах из A и обладающая

А3*. Для несовместных событий A1, ,An, верна аксиома аддитивности:

Эквивалентным аксиоме А3* является требование аддитивности А3 и аксиома непрерывности А4. Функция множеств P A 0 непрерывна, т.е. для любой монотонной последовательности

j 1

Предел существует по теореме о монотонной сходимости.

Пример 2. Распределение на непрерывном множестве R можно задать, определив вероятности на открытых интервалах ,x по правилу: P ,x F x с помощью функции

распределения F x , обладающей свойствами:

1)неубывающая и непрерывная слева,

2)0 F x 1.

Следствия из аксиоматического определения вероятности.

1. Формула сложения вероятностей для несовместных событий:

Опр. События образуют полную группу (разбиение), если несовместны, а в результате испытания может произойти только одно из них.

2.Свойство полной группы событий:

P A1 P An 1

3.Сумма вероятностей противоположных событий равна 1.

4.Вероятность невозможного события равна 0.

5.Для любых событий A и B справедлива формула сложения вероятностей

P A B P A P B P AB

n n

6.P Ak 1 P Ak

P Ai P AAi j P AAi j Ak