20. Задача о максимальном потоке. Остаточная сеть. Аугментальный (увеличивающий) путь. Алгоритм Форда-Фалкерсона.

Задача о максимальном потоке.

Сеть – это ориентированный взвешанный граф G = (v,e) с положительными весами ребер с(е), в котором есть ровно одна вершина – источник (S) и ровно одна вершина – сток (T).

Вершины не равные S и Т называются внунтренними,

Вес ре6ра с(e) – пропускная способность ребра.

Потоком называется функция f, которая переводит множество ребер в множество действительных чисел.

Функция f удовлетворяет:

1. Для любого ребра e € E: 0<=f(e)<=c(e)

2. Для всех v€ V,v<>S,v=T:div+ (v) =div_(v), где

• div+ - суммарный поток по всем ребрам е, таким что е=(u,v) div+(v) =,e=(u,v) – величина входящего потока

• div_ - величина исходящего потока div_(v) =,

Свойство потока: div_(S)=div+(T)

Величина div_(S)=div+(T) называется величиной потока в сети.

Задача о максимальном потоке.

Найти поток, величина которого не меньше величины любого другого потока (найти поток с максимальной величиной)

Остаточная сеть.

Пусть дана сеть G и в ней запущен поток f, остаточная сеть – это взвешенный ориентированный граф с множеством вершин V и множеством дуг, определяющих:

1. если в сети G есть ребро (u,v) и величина потока по этому ребру меньше с(е), то в остаточной сети есть ребро e=(u,v) с весом с(е)-f(e) –прямые ребра

2. если в Gесть ребро е=(u,v) и поток через это ребро >0, то в остаточной сети есть реброe’=(u,v) с весомf(e) –встречные ребра

Аугментальный (увеличивающий) путь.

Если в остаточной сети существует ориентированный путь из S в T, то в исходной сети можно увеличить поток вдоль этого пути. При этом проход по прямым ребрам - увеличение потока в данном ребре исходной сети, а по встречному ребру – уменьшение потока.

Алгоритм Форда-Фалкерсона

1. Запустить 0-й поток f(e)=0

2. Построить остаточную сеть

3. Найти в остаточной сети ориентированный путь из S в T

4. Если путь найден, то увеличить поток вдоль этого пути и перейти к шагу 2. Иначе конец алгоритма. Текущий поток является максимальным.

21. Задача о максимальном потоке минимальной стоимости (МаПМиС). Алгоритм решения.

Пусть существует сеть и каждому ребру приписана стоимость S(e). Стоимость потока через ребро равна S(e)*f(e). Стоимость потока в сети – суммарная стоимость потока через все ребра

Задача о МаПМиС заключается в поиске такого max потока, стоимость которого не превышает стоимость любого другого max потока. (в дальнейшем рассматриваются только maxпотоки)

При построении остаточной сети будем отмечать не только пропускные способности ребер, но и их стоимость. Для прямых ребер стоимость равна стоимости исходного ребра. Для встречных: стоимость противоположна стоимости исходного ребра.

Алгоритм:

1. Построить максимальный поток

2. Построить остаточную сеть со стоимостями

3. Найти в остаточной сети ориентированный цикл с отрицательной стоимостью

4. Если цикл найден, то увеличивается вдоль него поток. Иначе конец. Текущий поток – МаПМиС

Определение транспортной сети.

22. Метод ветвей и границ. Решение задачи «о рюкзаке» методом ветвей и границ.

Пусть Q– задача минимизации

S– множество допустимых решений

φ(S) – качество решения

Задача: найти S* такое, чтоφ(S*) – минимальное.

Метод:

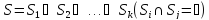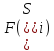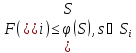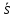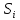Разбиваем Sна подмножества. Для всех подмножеств строится оценкатакое, что. Если найденотакое, что, то все решения израссматривать не нужно.

Задача «о рюкзаке»

Дано:

nпредметов

Веса:

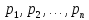
Стоимости:

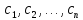
Рюкзак вместимостью V

Ограничение: .

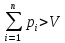Найти:

Множество предметов M: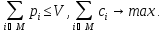

Задача является NP-полной.

1 способ:

1. Рассчитать ценность предметов

2. Упорядочить предметы по уменьшению ценности.

3. Ветвление (бинарное):

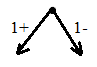
S₁– 1-ый предмет берем

S₂– 1-ый предмет не берем

4. Оценка:

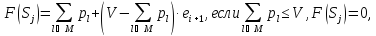иначе.

где M– множество предметов, которые уже взяли;

i+1 – номер очередного, еще не рассмотренного, предмета.

5. Выбираем вершину с максимальной оценкой, изменяем значение iи переходим к п.3

Пример:

4 предмета, V=5

Вершины графа пронумерованы сверху вниз слева направо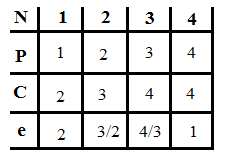

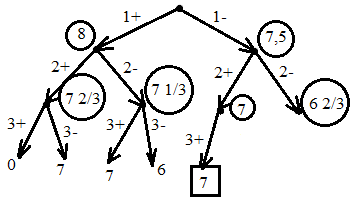
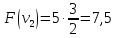
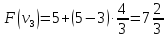
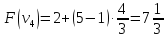
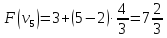
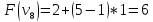
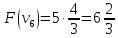
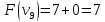
Ответ: набор {2;3}.

2 способ:

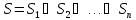
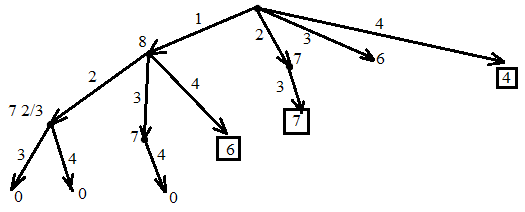
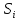- попадают все случаи, когда минимальный набор предметов, сложенных в рюкзак, равенi. Наj-ом шаге ветвление аналогично, но рассматриваем не минимальный номер, аj-ый по величине.

Вершины графа пронумерованы сверху вниз слева направо

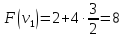
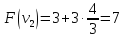
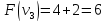
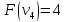
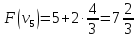
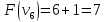
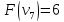
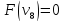
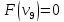
Ответ: {2,3}