1. Понятие сложности алгоритма. Верхняя, нижняя и средняя оценки сложности.

Способы оценки сложности:

1. Экспериментальные исследования.

Основные требования:

- множество разнообразных тестов с неповторяющимися закономерностями; - в наборе тестов должны присутствовать все «крайние» случаи;

- преимущество «обычных» входных данных.

Основные недостатки:

- сложность экстраполяции на другие объемы данных;

- занимает длительное время;

- результаты сильно зависят от конкретной реализации.

2. Теоретическая оценка.

Важно уметь строить теоретическую оценку сложности алгоритма. Кроме того, для приближенных алгоритмов важно оценивать точность приближенного решения.

На сложность алгоритма может влиять не только сама задача, но и ограничения на входные данные.

Понятие сложности алгоритмов:

1. Временная: оценивается

2. Емкостная: характеризует объем памяти, необходимый для хранения входных и выходных данных и промежуточных результатов.

x– входные данные

t_α(х)– функция сложности – оценка времени работы алгоритма на входных данных х.

Перейдем от х к характеристике входных данных v(x), которую будет называть объемом (сложностью) входных данных.

t_α(v)– сложность алгоритма

Пример:

function (n: integer): integer

var i,p: integer;

begin

p:=1; 1 оп

for i:=2 to n do p:=p*I n-1 раз по 2

f:=p; 1 оп

end;

итого: 1+(n-1)*2+1=2nопераций

V(n) – значение числаn

t_α(v)=2n

Верхняя (нижняя) оценка сложности алгоритма (t_α(v)) – это функция, отражающая максимальное (минимальное) количество операций, выполняемое алгоритмом при поступлении на вход данных объемомV, т.е. это их оценка в худшем (лучшем) случае.

Средняя оценка сложности 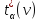- это функция, отражающая среднее количество операций, выполняемое алгоритмом при поступлении на вход данных объемомV, при этом при вычислении среднего количества учитывается вероятность появления тех или иных входных данных.

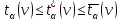
По умолчанию подразумевают среднюю оценку сложности. Ее сложнее всего получить.

Если не оговорено отдельно, то за одну условную операцию будем считать каждую арифметическую или логическую операцию, а также операции пересылки данных.

2 . Основные правила вычисления сложности алгоритма (сложность линейного алгоритма, ветвления, цикла). Примеры

Сложность алгоритма удобно оценивать по блок-схеме или ее упрощенному варианту – управляющему графу.

Линейные алгоритмы

Ветвление

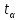
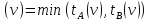
B

A

t_A

t_B

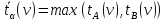
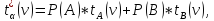
М_А – количество данных, при котором алгоритм идет по ветке А.

Цикл

1) заранее известно количество повторений

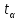
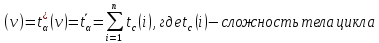
2) заранее неизвестно количество повторений

Универсальных методов нет

Пример. Бинарный поиск в упорядоченном массиве

function bin_find (m:mas; n,x: integer): integer;

var l,r,mid: integer;

begin

l:=1; r:=n; 2 оп

while l<r do

begin

mid:=(l+r) div 2; 3 оп

if x>m[mid] then max 3 оп

l:=mid+1 min 2 оп

else r:=mid; mid 1/2*2+1/2*3=2,5 оп

end;

if m[l]=x then bin_find:=l 2 оп

else bin_find:=0;

end;

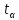
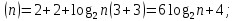
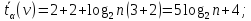
3. Реккурентные соотношения с постоянными коэффициентами

Однородные реккурентные соотношения

- реккурентное соотношение глубины 1

Решение однородных реккурентных соотношений

с_ka_n+k + c_k-1a_n+k-1 + … +c₁a_n+1+c₀a_n= 0 – общий вид о.р.с. глубины k

с_i - константы

a_i - искомая последовательность

Сделаем переход к характеристическому уравнению:

с_kx^n+k+c_k-1x^n+k-1 + … +c₁xⁿ⁺¹+c₀xⁿ= 0

с_kx^k+c_k-1x^k-1 + … +c₁x+c₀= 0 – хар. уравнение

1. Все корни разные

Пусть корни будут такие: a₁,a₂, …,a_k - k – штук

Тогда решение рек. соотношения будет иметь вид:

x_n = A₁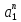 + A₂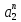 + … + A_k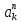

где константы A_i можно найти, исходя из начальных условий(например a₀= 1,a₁= 2)

2. Характеристическое уравнение имеет кратные корни, например хар-кое уравнение (x- 1)³= 0 имеет 1 корень кратности 3.

Пусть хар-кое уравнение имеет корни a₁,a₂, …,a_m кратностиr₁,r₂, …,r_m. Тогда общий вид решения будет следующим:

x_n = P₁(n)+ P₂(n)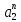+ … +P_m(n)

где P_i(n) – многочлен степени(r_i- 1). Коэффициенты многочленов P₁(n), P₂(n), …, P_m(n) находятся из начальных условий.

Решение неоднородных реккурентны соотношений

с_ka_n+k + c_k-1a_n+k-1 + … +c₁a_n+1+c₀a_n=f(n) – общий вид неоднородных рек. с.

Рассмотрим метод решения, когда f(n):

1) f(n) = P(n) - многочлен

2) f(n) = caⁿ, где с – константа, a ≠ 1

3) f(n) = P(n)aⁿ, где P(n) - многочлен

Решение состоит из 2х этапов:

1. Решение однородного реккурентного соотношения без учета начальных условий

2. Находим частные решения неоднородного реккурентного соотношения(неопределенные коэффициенты ищутся подстановкой ч. решения в неод. рек. соотношение)

Тогда 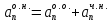, где решение однородного соотншения, найденное на 1ом этапе, а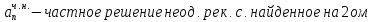этапе. После этого неопределенные коэффициенты ищутся исходя из начальных условий.

Правила нахождения частного решения неоднородного рек. соотношения:

1) f(n) = P(n)

Если a = 1 является корнем хар. ур. Кратности r, то частное решение н.р.с. имеет вид:

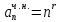Q(n),где многочленQ(n)имеет степень такую же, как иP(n)(есть резонанс)

2) f(n) = caⁿ, где с – константа,a ≠ 1

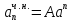,a ≠ 1(нет резонанса)

3) f(n) = P(n)aⁿ, гдеP(n)- многочлен

Q(n),a ≠ 1, где многочленQ(n) имеет степень такую же, как и P(n) (нет резонанса)