1. Изоморфизм линейных пространств

2. Следствия из теоремы об изоморфизме линейных пространств.

3. Ранг матрицы. Теорема о базисном миноре. Следствия. Теорема о ранге матрицы.

4. Практическое нахождение ранга матрицы.

5. Теорема о матрице перехода.

6. Преобразование координат вектора.

7. Подпространство. Теорема о подпространстве.

8. Связь между подпространствами и линейными оболочками.

9. Теорема о базисе и размерности линейной оболочки. Следствия.

10. Теорема Кронекера – Капелли.

11. Обоснование способа решения систем линейных уравнений с помощью ранга матрицы.

12. Свойства решений системы линейных однородных уравнений. Пространство решений. ФСР.

13. Теорема о ФСР. Следствия. Общее решение системы линейных однородных уравнений.

14. Свойства решений неоднородной системы линейных уравнений. Общее решение.

15. Сумма подпространств. Свойства.

16. Пересечение подпространств. Свойства.

17. Прямая сумма подпространств. Теоремы.

18. Представление линейного пространства в виде прямой суммы подпространств.

19. Линейный оператор, его свойства. Матрица линейного оператора. Образный оператор.

20. Связь матриц линейного оператора в разных базисах.

21. Связь координат вектора и его образа.

22. Теоремы о задании линейного оператора.

23. Сложение линейных операторов. Свойства.

24. Умножение линейного оператора на число. Свойства.

25. Умножение линейных операторов. Свойства.

26. Ядро линейного оператора. Свойства.

27. Область значений линейного оператора. Свойства.

28. Характеристический многочлен матрицы, характеристические числа матрицы, их количество. Подобные матрицы, их характеристические числа.

29. Характеристические корни линейного оператора.

30. Собственные векторы и собственные значения линейного оператора. Примеры. Свойства.

31. Собственные векторы, отвечающие различным собственным значениям.

32. Теорема о связи собственных значений линейного оператора и его характеристических корней.

33. Практическое нахождение собственных значений и собственных векторов линейного оператора.

34. Линейный оператор простой структуры, с простым спектром, его матрица. Приведение матрицы к диагональному виду. Каноническая форма матрицы. Теорема.

35. Квадратичная форма, её запись, матрица, ранг. Квадратичная форма при линейном преобразовании неизвестных, её ранг.

36. Канонический вид квадратичной формы. Основная теорема о квадратичных формах.

37. Нормальный вид действительной и комплексной квадратичной формы. Теоремы.

38. Закон инерции действительных квадратичных форм.

39. Положительно определенная квадратичная форма. Теорема. Критерий Сильвестра.

40. Евклидово пространство. Свойства. Примеры. Теорема о превращении линейного пространства в евклидово. Унитарное пространство.

41. Ортогональные системы векторов, ортонормированный базис, его свойства.

42. Процесс ортогонализации.

43. Теорема о существовании ортонормированного базиса.

44. Сопряженные операторы.

45. Нормальный оператор.

46. Самосопряженный оператор.

47. Унитарный оператор.

48. Перспективное соответствие между плоскостью и связкой.

49. Однородные координаты точек на плоскости.

50. Проективная плоскость. Проективное пространство.

Вопрос1. Изоморфизм линейных пространств; его свойства; примеры. Теорема об изоморфизме.

Два действительных линейных пространства V и V’ называются изоморфными, если между их векторами установлено взаимно однозначное соответствие — всякому вектору а из V сопоставлен вектор а' из V’, образ вектора а, причем различные векторы из V обладают различными образами и всякий вектор из V служит образом некоторого вектора из V, — и если при этом соответствии образом суммы двух векторов служит сумма образов этих векторов,

(а + b)' = а' + b', (2)

а образом произведения вектора на число служит про из ведение образа этого вектора на то же число,

(αa)'= αа'. (3)

Отметим, что взаимно однозначное соответствие между пространствами V и V, удовлетворяющее условиям (2) и (3), называется изоморфным соответствием.

Так, пространство векторов-отрезков на плоскости, выходящих из начала координат, изоморфно двумерному векторному пространству, составленному из упорядоченных пар действительных чисел: мы получим изоморфное соответствие между этими пространствами, если на плоскости фиксируем некоторую систему координат и всякому вектору-отрезку сопоставим упорядоченную пару его координат.

Докажем следующее свойство изоморфизма линейных пространств: образом нуля пространства V при изоморфном соответствии между пространствами V и V’ служит нуль пространства V'.

Пусть, в самом деле, а будет некоторый вектор из V, а'—его образ в V’. Тогда, ввиду (2),

a' = (a + 0)' = a'+0', т. е. 0' будет нулем пространства V’. ■

ч2.Вопрос2. Следствия из теоремы об изоморфизме линейных пространств.

Следствие 1: любое n мерное пространство изоморфно

Следствие 2: критерий изоморфизма линейных пространств:

Два конечномерных линейных пространства L1 и L2 изоморфны тогда когда они имеют одинаковые размерности.

Доказательство:

1. пусть L1 изоморфно L2 => базис переходит в базис и базисы состоят из ровного числа векторов

2. Пусть dim(L1 и L2) совпадают

Пространство L1 при помощи изоморфа φ1 изоморфно

Пространство L2 при помощи изоморфа φ2 изоморфно

РL2 => L1 L2 ■

Следствие 3: система векторов а1,а2,…,as конечномерного линейного пространства над полем Р линейно зависима тогда и только тогда когда зависима система ее координат столбцов.

Пример:

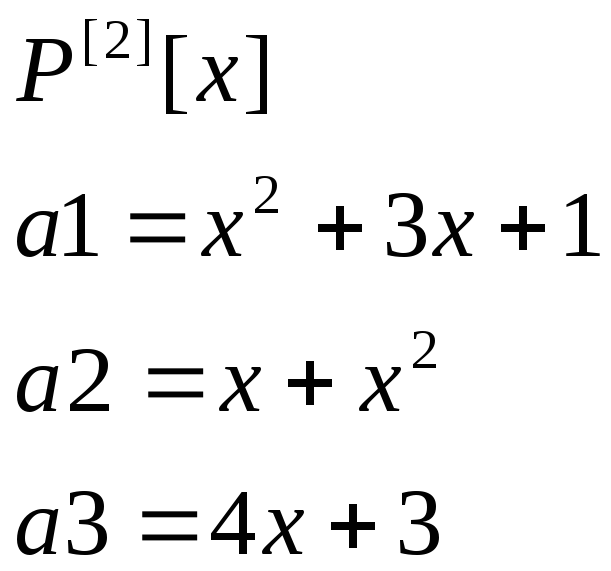
r = 3 => a1,a2,a3 – л/нз.

ч2.Вопрос3. Ранг матрицы. Теорема о базисном миноре. Следствия. Теорема о ранге матрицы.

Пусть дана матрица A=

(a11,a12,...,a1n)

(a21,a22,...,a2n)

(.......................)

(as1,as2,....,asn)

содержащая s строк и n столбцов, причем s и n никак не связаны между собой. Столбцы этой матрицы рассматриваемые как s-мерные векторы, могут вообще говоря быть линейно независимыми . Ранг системы столбцов т.е. максимальное число линейно независимых столбцов матрицы A (число столбцов входящих в любую максимально линейно независимую подсистему системы столбцов), называется рангом этой матрицы.

Подобным образом можно рассматривать строки матрицы как n-мерные векторы и ранг системы строк равен рангу системы столбцов, и равен рангу этой матрицы.

Понятие минора. Выберем в матрице A произвольные k строк и k столбцов, k=min(s,n).

Элементы стоящие на пересечении этих строк и столбцов, составляют квадратную матрицу порядка k , определитель которой называется минором k-го порядка матрицы A. Дальше нас будут интересовать миноры отличные от нуля, а именно наивысший порядок отличных от нуля миноров. При его разыскании полезно учитывать след. замечание:

Если все миноры k-го порядка матрицы A равны нулю то равны нулю все миноры более высоких порядков. В самом деле разлагая всякий минор порядка k+j , k<k+j<=min(s,n) на основании теоремы Лапласа, по любым k строкам мы представим этот минор в виде суммы миноров порядка k , умноженных на некоторые миноры порядка j, и этим докажем что он равен нулю. Теорема о ранге матрицы. Наивысший порядок отличных от нуля миноров матрицы A равен рангу этой матрицы.

Док-во: Пусть наивысший порядок отличных от нуля миноров матрицы A равен r. Предположим,- чтол не нарушает общности доказательства,- что минор r-го порядка D, стоящий в левом верхнем углу матрицы A=

(a₁₁ ... a_1r | a_1,r+1 ... a_1n)

(.... D ..... | ....... ....... ........)

(a_r1 ... a_rr | a_r,r+1 ... a_rn)

(a_r+1,1 ... a_r+1,r a_r+1,r+1 ... a_r+1,n)

( . . . . . )

(a_s1 ... a_sr a_s,r+1 ... a_sn)

отличен от нуля, D =/=0. Тогда первые r столбцов матрицы A будут между собой линейно независимы: если бы между ними существовала линейная зависимость, то , как при сложении векторов складываются соответствующие компоненты, между столбцами минора существовала бы эта же линейная зависимость и поэтому минор D был бы равен нулю. Докажем теперь что всякий L столбец матрицы A, r<L<=n, будет линейной комбинацией первых r столбцов. Берем любое i 1<=i<=s, и строим вспомогательный определитель G (r+1)-го порядка

G=

|a₁₁ ... a_1r a_1L|

|…. ... .... ..... |

|a_r1 ... a_rr a_rL |

|a_i1 ... a_ir a_iL |

, получающийся окаймлением минора D соответствующими элементами L-го столбца и i-й строки. При любом i определитель G равен нулю. Действительно, если i>r, то G , будет минором (r+1)-го порядка матрицы A и поэтому равен нулю ввиду выбора числа r. Если же i<=r , то G уже не будет минором матрицы A , так как не может быть получен вычеркиванием из этой матрицы некоторых её строк или столбцов : однако определитель G будет содержать теперь две равные строки, и следовательно снова равен нулю. Рассмотрим алгебраические дополнения элементов последней строки определителя G. Алгебраическим дополнением для элемента aiL служит минор . Если 1<=j<=r, то алг. дополнением для aij в G будет число

|a₁₁ ... a_1,j-1 a_1,j+1 ... a_1r a_1L|

Aj=(-1)^(r+1)+j |... ... .... ..... .. ...|

|a_r1 ... a_r,j-1 a_r,j+1 ... a_rr a_rL|

Таким образом разлагая определитель G по его последней строке и приравнивая это разложение к нулю, так как G=0 получаем: aj1A1+aj2A2+...+airAr+aiLD=0 откуда ввиду D=/=0 aiL= - (A1/D)ai1 – (A2/D)ai2 - ... – (Ar/D)air это равенство справедливо для всех i, i=1,2...s, атак как его коэффициенты от i не зависят, мы получаем что весь L-й столбец матрицы A будет суммой её первых r столбцов, взятых с коэффициентами –(A1/D), - (A2/D),... , - (Ar/D). Таким образом в системе столбцов матрицы A мы нашли максимальную линейно независимую подсистему, состоящую из r столбцов. Этим доказано, что ранг матрицы A равен r, т.е. доказана теорема о ранге. ■

Следствие1: Максимальное число линейно независимых строк всякой матрицы равно максимальному числу её линейно независимых столбцов т.е. равно рангу этой матрицы.

Для доказательства транспонируем матрицу сохраняя нумерацию. При этом максимальный порядок отл. От нуля миноров не может поменяется т.к. трансп. Не меняет определителя, а для всякого минора исходной матрицы минор , полученный из него транспонированием, содержится в новой матрице и обратно. Отсюда следует что ранг новой матрицы равен рангу исходной матрицы, и равен максимальному числу линейно независимых столбцов новой матрицы, т.е. равен макс. Числу линейно нез. строк исходной матрицы.

Следствие 2: Определитель n-го порядка равен нулю  когда между его строками существует лин.зависимость. В одну сторону это утверждение доказывается по свойству 8 определителя( Если одна из строк определителя есть линейная комбинация его других строк , то определитель равен нулю.) Обратно: пусть нам дан определитель n-го порядка равный нулю. Отсюда следует что наивысший порядок отличных от нуля миноров этой матрицы меньше n. т.е. ранг меньше n а поэтому на основании доказанном выше строки этой матрицы линейно зависимы. (в формулировке доказанного сейчас следствия вместо строк можно говорить о столбцах).

ч2.Вопрос5. Теорема о матрице перехода.

Пусть в n-мерном линейном пространстве V заданы базисы e₁,e₂,…,e_n (**) и e₁’,e₂’,…,e_n’ (***). Каждый вектор базиса (***), как и всякий вектор пространства V, однозначно записывается через базис (**), e₁’=τ_1je_j, e₂’= τ_2je_j,… , e_n’=τ_nje_j , i=1,2,…,n. (e_i’=Στ_ije_j.). Матрица

τ₁₁… τ_1n

T= …………

τ_n1… τ_nn

строки которой являются строками координат векторов (***) в базисе (**), называется матрицей перехода от базиса (**) к базису (***). Связь между базисами (**) и (***) и матрицей перехода T, можно записать в виде матричного равенства

e₁’ τ₁₁ τ₁₂ … τ_1n e₁

e₂’ τ₂₁ τ₂₂ … τ_2n e₂

. = …………… .

e_n’ τ_n1 τ_n1 … τ_n e_n

или e’=Te. С другой стороны, T’ – матрица перехода от базиса (***) к базису (**), то

e=T’e’. Отсюда e=(T’T)e, e’=(TT’)e’, т.е. в виду линейной независимости базисов e и e’, T’T=TT’=E, откуда T’=T^-1. Этим доказано что матрица перехода всегда является невырожденной матрицей.

Связь координат …

Пусть в n-мерном линейном пространстве даны базисы (**) и (***) с матрицей перехода T=( τ_ij), e=Te’. Найдём связь между строками координат произвольного вектора a в этих базисах. Пусть a=Σα_jej, a=Σα_i’e_i’ (#). Заменяем e_i’ получаем a=Σα_i’(Στ_ije_j)=Σ(Σα_i’τ_ij)e_j. Сравнивая с (#) получаем: a_j=Σα_i’τ_ij, j=1..n, т.е. имеет место матричное равенство (α₁,α₂,…,α_n)=(α₁’,α₂’,…,α_n’)T. Таким образом, строка координат вектора a в базисе e равна строке координат этого вектора в базисе e’, умноженной справа на матрицу перехода от базиса e к базису e’. Отсюда следует равенство (α₁’,α₂’,…,α_n’)= (α₁,α₂,…,α_n)T^-1. ■

ч2.Вопрос6. Преобразование координат вектора.

Пусть в ЛП L выбраны 2-а базиса е и е’ и вектор а. Обозначим координаты вектора а в базисе е столбцом. e: e₁, e₂… e_n

_{в е}

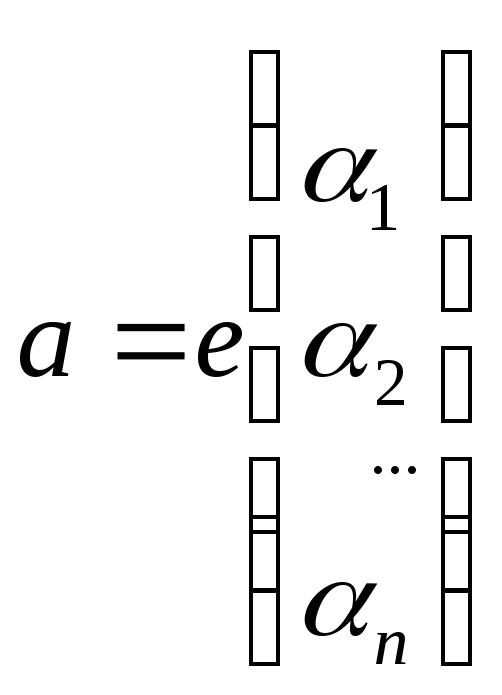_{в е’}

_{в е}

_{в е’}

тогда _{== (еТ)}

_e’=eT

_{т.к. умножение матриц ассоциативно, то скобки можно переставить}

_{= е[T] =>=T}

_{и по заданной матрице Т заданным координатам вектора а в базисе е’ можем найти координаты вектора а в базисе е’.}

_{ae’: =T}^-1

ч2.Вопрос7. Подпространство. Теорема о подпространстве.

Подмножество L линейного пространства V называется линейным подпространством этого пространства, если оно само является линейным пространством по отношению к определенным в V операциям сложения векторов и умножения вектора на число.

Так, в 3-х мерном евклидовом пространстве совокупность векторов, выходящих из начала координат и лежащих на некоторой плоскости (или некоторой прямой), проходящей через начало, будет линейным подпространством.

Для того чтобы непустое подмножество L пространства V было его линейным подпространством, достаточно выполнения следующих требований:

1.Если векторы а и в принадлежат к L, то в L содержится и вектор а+в.

2.Если вектор а принадлежит к L, то в L содержится и вектор αа при любом значении числа α.

Действительно, ввиду условия 2, множество L содержит нулевой вектор: если вектор а принадлежит к L , то L содержит и вектор 0*а=0. Далее,L вместе со всяким своим вектором а содержит , снова ввиду свойства 2, и противоположный ему вектор –а=(-1)*а, а поэтому ввиду свойства 1 к L принадлежит и разность любых двух векторов из L. Что же касается требований, входящих в определение линейного пространства, то они , выполняясь в V, будут выполняться и в L.

Примерами линейных подпространств могут служить множество векторов на прямой или на плоскости(в обычном трехмерном пространстве); множество многочленов степени не выше второй являются подпространством в линейном пространстве многочленов степени не выше третьей.

Пусть в линейном пространстве V над полем P дана система векторов

а₁,а₂,…,а_{r (1)}

Множество всевозможных линейных комбинаций α₁а₁+α₂а₂+…+α_rа_r этой системы называют линейной оболочкой системы векторов а₁,а₂,…,а_r.

Докажем, что L будет линейным подпространством. В самом деле, если в=α₁а₁+α₂а₂+…+α_rа_r

с=β₁а₁+ β₂а₂+…+β_rа_r

то

в+с=( α₁₊β₁) а₁₊( α₂₊+β₂)а₂+…+ (α_r+β_r)а_r ,

т.е вектор в+с принадлежит к L: к L принадлежит и вектор

γв=(γα₁)а₁+(γα₂)а₂+…+(γα_r)а_r

при любом числе γ.

Линейную оболочку L системы векторов а₁,а₂,…,а_r также называют подпространством, порожденным этой системой векторов, или подпространством, натянутым на эту систему векторов и обозначают

L={ а₁,а₂,…,а_r }

ч2.Вопрос8. Связь между линейным подпространством и линейными оболочками

Опр.: Пусть задана конечная система векторов a₁,a₂,…a_n из L, множество векторов вида M={_{, где} наз-я линейной оболочкойa₁,a₂,…a_s

Дополнительное обозначение L(a₁,a₂,…a_s) = < a₁,a₂,…a_s >

Док-во: Пусть в L заданы векторы a₁,a₂,…as Покажем, что для линейной оболочки векторов a₁,a₂,…as выполнены замкнутость + и * на число

Пусть а и b - два произвольных элемента из линейной оболочки, тогда они представимы в виде

а =

_{b =}

_{сумма a+b=}

_{т.к. есть замкнутьсть + => входит в Р}

_{аналогично проверяем замкнутость по *}

_pa=

_{т.к значит принадлежит М}

_{замкнутость +,* выполнена=> данное множество ЛПП}

_{ч2.Вопрос9. Теорема о базисе и размерности линейной оболочки. Следствия}

Т.к. a1,a2,…as - конечная, то ее ранг тоже конечен. <=s

a_s<=s => найдется r-векторов из этой системы, то каждый из векторов a₁,a₂,…a_s представим в виде линейной комбинации, значит и любой элемент из линейной оболочки представим в виде линейной комбинации тех же самых векторов и ее размерность конечна.

Размерность линейной оболочки векторов a₁,a₂,…a_s равна рангу системы векторов a₁,a₂,…a_s

dim(L(a₁,a₂,…a_s))=r(a₁,a₂,…a_s)

Док-во в конечной системе a₁,a₂,…a_s всегда можно выбрать базис и число векторов в нем равно рангу системы a₁,a₂,…a_s . Не нарушая общности можно считать, то это будут первые r- векторов.

Пусть a₁,a₂,…a_r - базис a₁,a₂,…a_s Покажем, что эти вектора a₁,a₂,…a_r - будут базисом для линейной оболочки

Пусть а - произвольный вектор принадлежащий линейной оболочке

_что а =

каждый из векторов а_r+1, a_r+2 представим в виде линейной комбинации векторов a₁,a₂,…a_s - т.к. они были базисом для нашей системы

а_r+1 =

а_r+2 =

а_s =

Получили, что а - представим в виде линейной комбинации векторов

a₁,a₂,…a_{r -} будет базисом для линейной оболочки

Пространство L - может и не быть конечномерным, но любая его линейная оболочка будет конечномерной и ее размерность не превосходит числа векторов в порождающей системе

ч2.Вопрос10. Теорема Кронекера – Капелли. Шрифт глючит - не менять!

Система

a₁₁x₁ + a₁₂x₂+…+ a_1nxn =b₁

(1) a₂₁x₁ + a₂₂x₂+…+ a_2nxn =b₂ a_ijR

…………………………..

a_m1x₁ + a_m2x₂+…+ a_mnxn =b_m

совместна тогда и только тогда, когда ранг матрицы этой системы равен рангу расширенной матрицы.

Док-во: x₁⁰ , x₂⁰,…,x_n⁰ – решение

a₁₁x₁⁰ +…+ a_1nx_n⁰ =b₁

……………………… (*)

a_m1x₁ + …+ a_mnx_n⁰ =b_m

__n

A’ = a₁₁ … a_1n b₁

a_m1 … a_mn b_m

___n (**)

___n

Каждый вектор  линейно выражается через (***), а все векторы (***) линейно выражаются через (**)

x₁⁰_ + x₂⁰_ +…+x_n⁰_n линейно выражается через (**) т.е. каждый вектор из (***) линейно выражается (**) –> (**)~(***) , а ранги эквивалентных матриц равны  rang(A) = rang(A’)

Пусть ранги равны, т.е. rang(A) = rang(A’) = r выберем в (**) максимально линейно независимую систему ___r максимально линейно независимая подсистема из (**) эта система входит и в (***), она также максимальна --> она максимально линейно независима и в (***)  x₁⁰_ + x₂⁰_ +…+x_r⁰_r = x₁⁰_ + x₂⁰_ +…+x_r⁰_r +0 * _r+1 +…+0*_n расписав в координатном виде получим (*) и x_r+1 =…= x_n⁰=0 –>  (x₁⁰,x₂⁰ ,…,x_r⁰0 ,…,0) – решение системы (1)  система (1) совместна.

ч2.Вопрос11. Обоснование способа решения систем линейных уравнений с помощью ранга матрицы.

Правило. Пусть система совместна и М – минор максимального порядка не = 0. Для решения

1. остовляем в системе (1) те уравнения на пересечении строк которого стоит минор М, а остальные отбрасываем

2. Оставляем в левых частях те неизвестные на пересечении столбцов коэффициенты которых стоит минор М. Остальные переносим вправо. 3. Находим неизвестные в левых частях по правилу Крамера (выражаем их через свободные).

Выражение всех неизвестных через свободные называют общим решением системы.

ч2.Вопрос12. Свойства решений системы линейных однородных уравнений. Пространство решений. ФСР. Шрифт глючит - не менять!

Система

a₁₁x₁ + a₁₂x₂+…+ a_1nxn =b₁

(1) a₂₁x₁ + a₂₂x₂+…+ a_2nxn =b₂ a_ijR

…………………………..

a_m1x₁ + a_m2x₂+…+ a_mnxn =b_m

называется однородной, если все правые части b₁=b₂=…=b_m=0. Если r=n система имеет единственное только нулевое решение. Если r<n - бесконечно много решений.

a₁₁x₁ + a₁₂x₂+…+ a_1nxn =0

(8) a₂₁x₁ + a₂₂x₂+…+ a_2nxn =0 a_ijR

…………………………..

a_m1x₁ + a_m2x₂+…+ a_mnxn =0

Множество всех наборов, стоящих слева, образуют n-r мерное арифметическое пространство. Множество всех наборов, стоящих справа, образуют пространство решений системы (8). Размерность пространства решений системы (8) не превышает n.

Пространство решений имеет (n-r) –размерность. Решение линейной однородной системы уравнений любая максимально л/н система имеет (n-r) решений. Максимально л/н система решений для системы однородных уравнений называют её фундаментальной системы решений.

x⁽¹⁾= (x₁’,x₂’,…,x_n’)

x⁽²⁾= (x₁’’,x₂’’,…,x_n’’) фундаментальная система (8)

x^(n-r)= (x₁^(n-r),x₂^(n-r),,…,x_n^(n-r),)

Тогда для любого решения X X= x⁽¹⁾_ + x₂⁽²⁾_ +…+_n-rx^(n-r) где _iR

Для того чтобы найти фундаментальную систему достаточно свободным неизвестным придать (n-r) значений так, чтобы определитель, составленный из них был отличен от нуля.

X_r+1’ x_r+2’ x_n’

X_r+1’’ x_r+2’’ x_n’’ 0

X_r+1^(n-r) x_r+2^(n-r) x_n^(n-r)

ч2.Вопрос14. Свойства решений неоднородной системы линейных уравнений. Общее решение.