Коллоидная химия

по геометрическому признаку:

3. по кинетическому состоянию ДФ

кинетическое состояние ДФ

свободнодисперсные связнодисперсные

(капиллярные тела)

Золи суспензии макропористые

микропористые (>200 нм)

(<2 нм) переходнопористые

Гели пасты (2 – 200 нм)

ДФ	ДС	Тип
Тв	Тв	Минералы
Тв	Ж	Коллоидные растворы
Тв	Г	Дым
Ж	Тв	Сок растений, почва
Ж	Ж	Эмульсии (молоко)
Ж	Г	Туман
Г	Тв	Твердые пены (капиллярно – пористые тела)
Г	Ж	Пены (мыльная)
Г	Г	Для коллоидной химии нет

4. по энергии взаимодействия ДС и ДФ:

• Лиофильные (сильное взаимодействие).

• Лиофрбные (слабое взаимодействие).

5. по величинам удельной поверхности:

- межфазовая поверхность

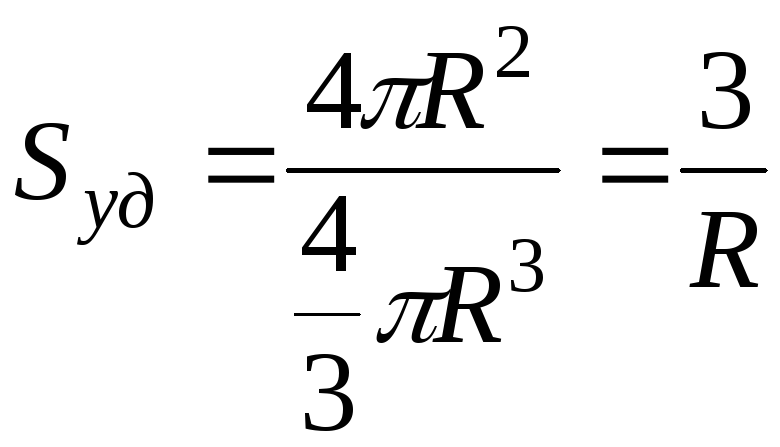- для частиц сферической формы (м^-1)

S_уд всегда очень большая величина.

Поверхностная энергия G_S:

–полная поверхностная энергия системы.

Поверхностная энергия может преобразовываться в энергию Гиббса, тепловую работу, механическую работу, в работу химическую, в электрическую энергию.

Свойства дисперсных систем:

1. Молекулярно – кинетические (диффузия, осмос, седиментация).

2. Оптические (светопоглощение и светорассеяние).

3. Электро-кинетические (электрофорес, электроосмос, потенциал седиментации, потенциал течения).

Молекулярно – кинетические свойства

МКТ рассматривает дисперсные системы с позиции истинных растворов, т. е. ДС – это растворитель, а ДФ – растворенное вещество. Выделяют следующие свойства: броуновское движение, осмос, седиментация. Для дисперсионных систем характерны два вида устойчивости:

• Агрегативное – устойчивость по отношению к слипанию.

• Седиментационная – по отношению к силе тяжести.

Седиментация.

Седиментация – это движение частиц под действием силы тяжести. Потеря седиментационной устойчивости ведет к расслаиванию системы.

В начальный момент времениmg>F_тр (равноускоренное движение).

В момент времени t, который соответствует установлению равновесие: .

Закон Стокса: 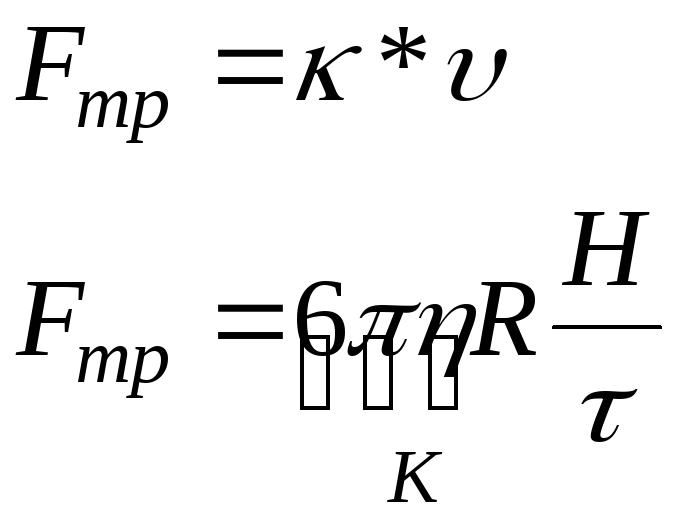, где

- коэффициент трения, R – радиус частицы, Н – высота, τ – время.

- плотность дисперсной фазы, - плотность дисперсионной среды

- основная формула седиментационого анализа: измеряя массы веществ, осевших в какой – либо момент времени, можно узнать размер этих частиц.

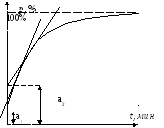
Кривая накопления (относительно изменения массы)- по ней находят кумулятивную фракцию - это доля частиц, осевших к данному моменту времени: .

Это отрезок, который отсекает на оси ординат касательная, проведенная к данной точке кривой накопления.

После диффиренцирования:

Максимум и точка перегиба совпадают:

Система называется монодисперсной, если в ней преобладают частицы одного размера; если двух размеров – бидисперсная:

Поли дисперсная:

Диффузия.

Диффузия – это процесс, направленный на выравнивание концентраций в первоначально неоднородной среде. По своей сути противоположен седиментации.

S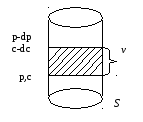 – площадь поперечного сечения, p-dp, c-dc.Давление и концентрация меньше, ν - расстояние

Два уровня. Движущей силой процесса диффузии выступает градиент осмотического давления:

. В состоянии равновесия и для первой частицы справедливо:, – из закона Стокса.

N – число частиц (Na), С – концентрация, ν – высота

. - число частиц в объеме, диф. поток в единице времени, ν – линейная скорость движения, высота к единице поверхности.

Получаем диффузионный поток: , т. к..

- 1-й закон Фика;

- уравнение Эйнштейна (коэффициент диффузии).

Поскольку все направления движения равновероятны, была предложена проекция среднеквадратичного сдвига:

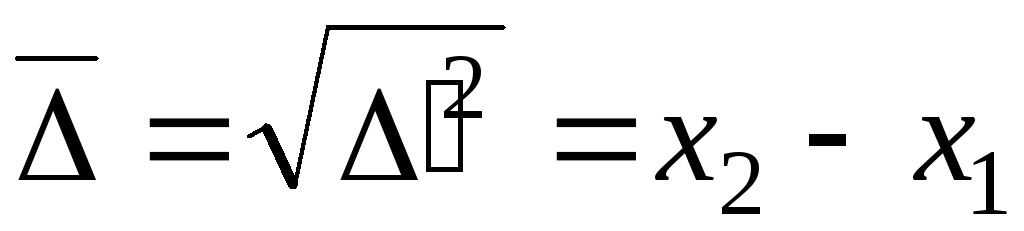, Идут вверх:; идут вниз:.

Переносимая масса:

диффузионный поток в единицу времени через единицу поперечного сечения.

- по 1 – му закону Фика.

,

- уравнение для среднеквадратичного сдвига

D ~ 10^-11 – 10^-14 м²/с, [D]=[м²/с]

Коэффициент диффузии – это поток вещества, переносимый через цилиндр с единичной площадью поперечного сечения в единицу времени.