
- •Методические указания и контрольные задания
- •Список литературы
- •Задание на контрольную работу
- •Методические указания к выполнению контрольной работы
- •Методические указания к выполнению третьего задания
- •Методические указания к выполнению четвертого задания
- •Варианты для выполнения первого задания
- •Варианты для выполнения второго задания
- •Варианты для выполнения третьего задания
- •Варианты для выполнения четвертого задания
- •Пример Задание №1 графический метод решения задач линейного программирования
- •Метод дихотомии.
- •Метод ''Золотого сечения''
- •Метод Фибоначчи.
- •Вариационное исчисление
- •Задание № 4
- •Контрольные вопросы
Метод дихотомии.
Шаг первый:
Интервал неопределенности делим пополам.
![]()
Находим точки, равноотстоящие от
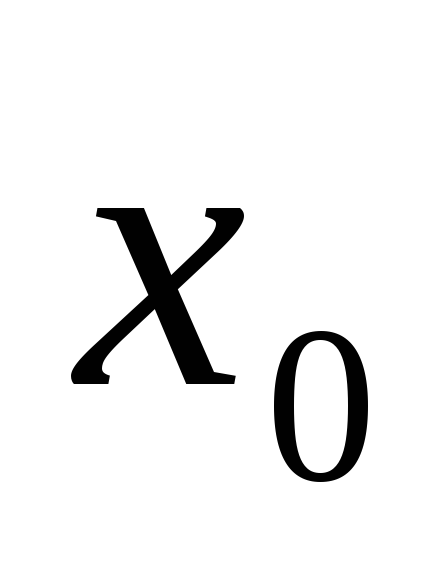 на
на раз.
раз.
![]()
Находим значения функции в точках
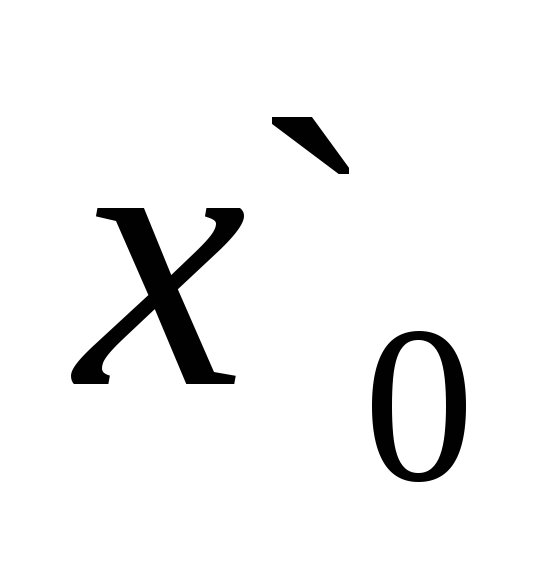 и
и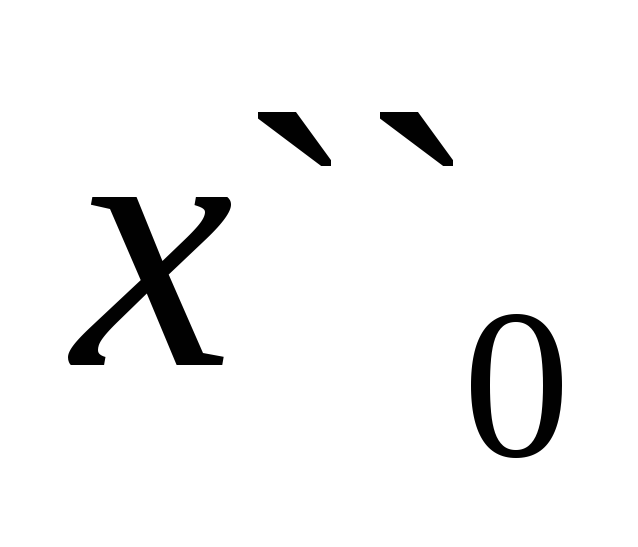
![]()
Отбрасываем ту часть неопределенности, в которой не может быть минимума. Отбрасываем часть отрезка левее
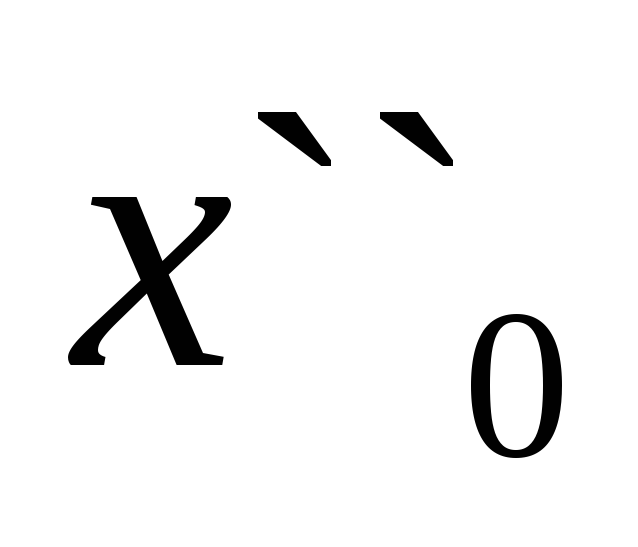 .
При этом интервал неопределенности
сокращается почти на половину.
.
При этом интервал неопределенности
сокращается почти на половину.
![]()
Определяем длину нового интервала неопределенности
![]()
Проверяем критерий окончания счета
![]()
Экстремум с заданной точностью не найден. Делаем, по крайней мере, еще один шаг.
Результаты следующих шагов.
Второй шаг:
![]()
Отбрасываем часть
отрезка левее
![]() .
При этом новый интервал неопределенности.
.
При этом новый интервал неопределенности.
![]()
![]()
Проверяем критерий
окончания счета. Так как
![]() ,
то делаем еще шаг.
,
то делаем еще шаг.
Третий шаг:
![]()
Отбрасываем часть
отрезка левее
![]() .
При этом новый интервал неопределенности.
.
При этом новый интервал неопределенности.
![]()
![]()
Проверяем критерий
окончания счета. Так как
![]() ,
то делаем еще шаг.
,
то делаем еще шаг.
Подобные
шаги проделываем до тех пор, пока не
выполнится критерий окончания счета.
Поскольку на данном интервале функция
монотонно убывает, то, очевидно, минимум
в точке
![]()
![]()
Метод ''Золотого сечения''
Шаг первый:
Определим координаты точек
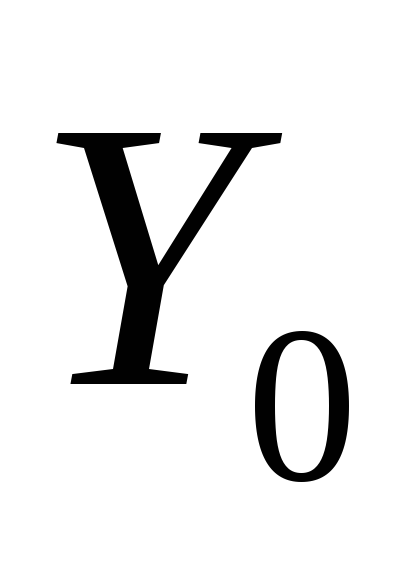 и
и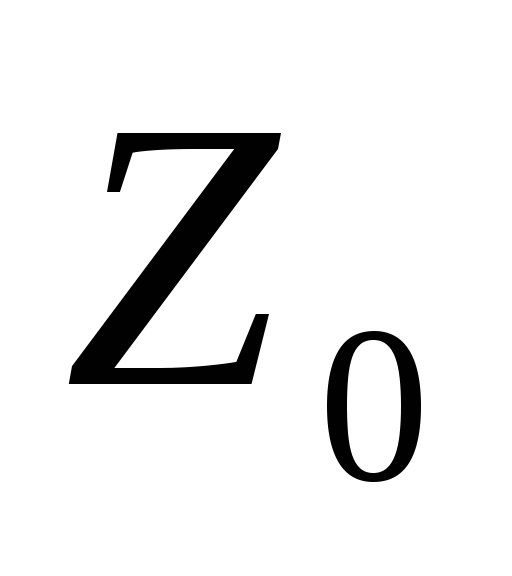
![]()
Вычисляется функция в точках
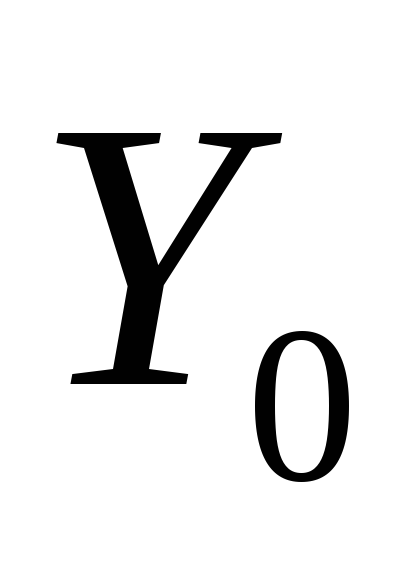 и
и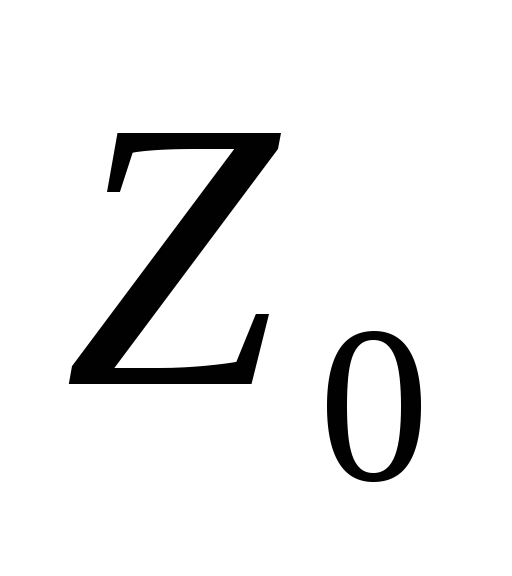
![]()
Отбрасываем часть отрезка левее
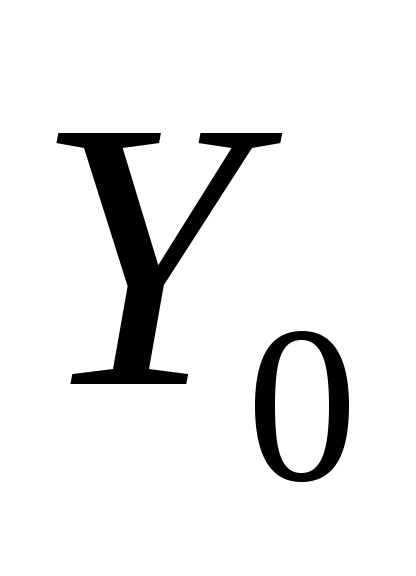 ,
так как там быть минимума не может. При
этом новый интервал неопределенности
,
так как там быть минимума не может. При
этом новый интервал неопределенности
![]()
Определим координаты точек
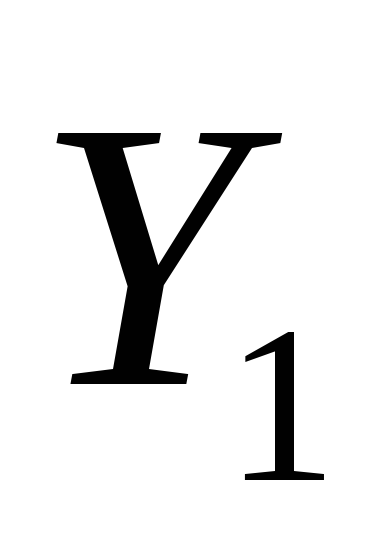 и
и
![]()
Определяем длину нового интервала неопределенности
![]()
Проверяем критерий окончания счета
![]()
Экстремум с заданной точностью не найден. Делаем, по крайней мере, еще один шаг.
Результаты следующих шагов.
Второй шаг:
![]()
Отбрасываем часть
отрезка левее
![]() .
При этом новый интервал неопределенности.
.
При этом новый интервал неопределенности.
![]()
![]()
![]()
Проверяем критерий
окончания счета. Так как
![]() ,
то делаем еще шаг.
,
то делаем еще шаг.
Третий шаг:
![]()
Отбрасываем часть
отрезка левее
![]() .
При этом новый интервал неопределенности.
.
При этом новый интервал неопределенности.
![]()
![]()
![]()
Проверяем критерий
окончания счета. Так как
![]() ,
то делаем еще шаг.
,
то делаем еще шаг.
Подобные
шаги проделываем до тех пор, пока не
выполнится критерий окончания счета.
Поскольку на данном интервале функция
монотонно убывает, то, очевидно, минимум
в точке
![]()
![]()
Метод Фибоначчи.
Этот метод имеет тот же алгоритм, что и метод ''Золотого сечения''. Отличия в определении координат начальных точек.
Шаг первый.
Определим координаты начальных точек.
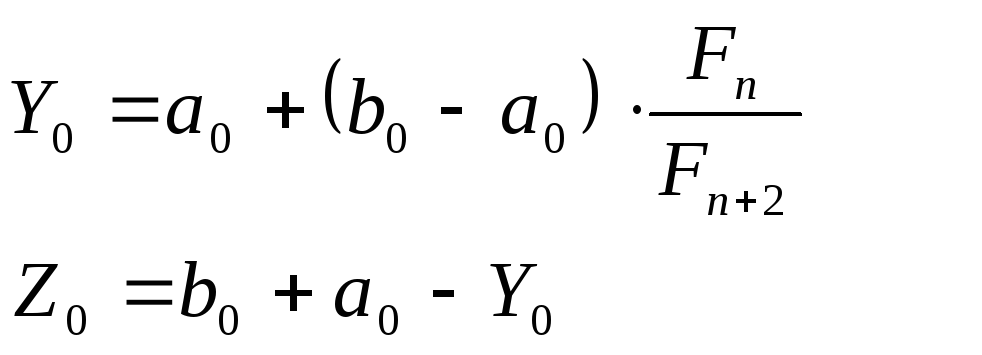
где
![]() ,
,![]() -n–oeи
(n+2)-ое числа Фибоначчи.
-n–oeи
(n+2)-ое числа Фибоначчи.
Эти числа определяются
по формуле
![]() .
.
Число nопределяется из соотношения![]() .
.
В нашем случае
![]()
Вычисляется функция в точках
 и
и
![]()
Отбрасываем часть отрезка левее
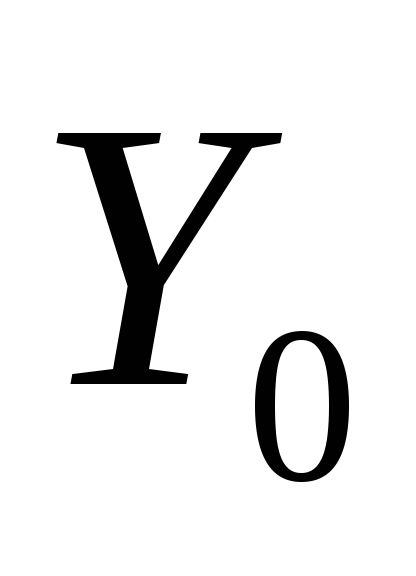 ,
так как там быть минимума не может. При
этом новый интервал неопределенности
,
так как там быть минимума не может. При
этом новый интервал неопределенности
![]()
Определим координаты точек
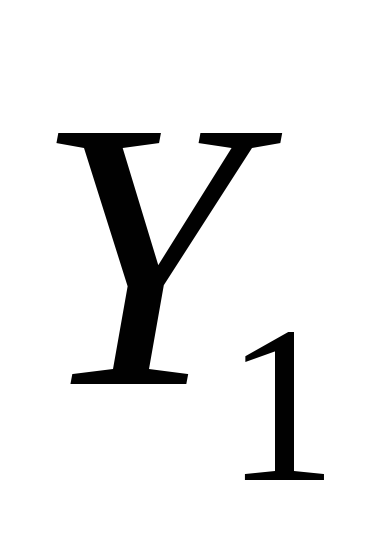 и
и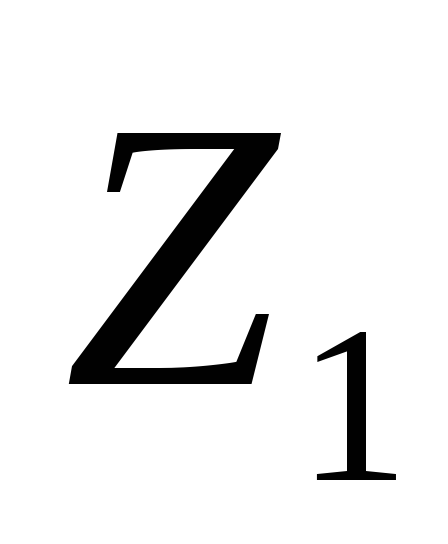
![]()
Определяем длину нового интервала неопределенности
![]()
Проверяем критерий окончания счета
![]()
Экстремум с заданной точностью не найден. Делаем, по крайней мере, еще один шаг.
Результаты следующих шагов.
Второй шаг:
![]()
Отбрасываем часть
отрезка левее
![]() .
При этом новый интервал неопределенности.
.
При этом новый интервал неопределенности.
![]()
![]()
![]()
Проверяем критерий
окончания счета. Так как
![]() ,
то делаем еще шаг.
,
то делаем еще шаг.
Третий шаг:
![]()
Отбрасываем часть
отрезка левее
![]() .
При этом новый интервал неопределенности.
.
При этом новый интервал неопределенности.
![]()
![]()
![]()
Проверяем критерий
окончания счета. Так как
![]() ,
то делаем еще шаг.
,
то делаем еще шаг.
Подобные
шаги проделываем до тех пор, пока не
выполнится критерий окончания счета.
Поскольку на данном интервале функция
монотонно убывает, то, очевидно, минимум
в точке
![]()
![]()
Задание № 3
