Варианты для выполнения второго задания

№ вар-та	[a0, b0]	f(x)	
1	[3,5; 4,5]		0,02
2	[1,5; 2]		0,01
3	[1; 1,5]		0,05
4	[-5; -4]		0,02
5	[0,5; 1]		0,05
6	[0; 1]		0,1
7	[-3; -2]		0,1
8	[0,1; 2]		0,01
9	[-1,5; -1]		0,01
10	[1,5; 2]		0,02
11	[0; 0,5]		0,01
12	[-1; 0]		0,1
13	[-1; 2]		0,01
14	[0; 3]		0,01
15	[1,5; 2]		0,02
16	[1,5; 2]	x4 +4x2 – 32x + 1	0,05
17	[0,5; 1]	x3 – 3sinx	0,05
18	[0,5; 1]	x2 + 3x (lnx –1)	0,05
19	[-3; -2]	(x + 1)4 – 2x2	0,05
20	[3; 5]	(x – 4)2 + lnx	0,01

Варианты для выполнения третьего задания

1. экстр.

.

2. экстр.

.

3. экстр.

.

4. экстр.

.

5. экстр.

.

6. экстр.

.

7. экстр.

.

8. экстр.

.

9. экстр.

.

10. экстр.

.

11. экстр.

.

12. экстр.

.

13. 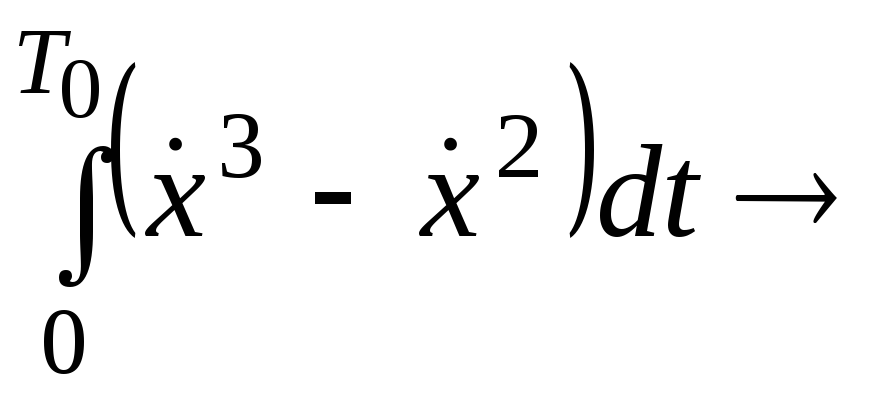экстр.

.

14. экстр.

.

15. экстр.

.

16. экстр.

.

17. экстр.

.

18. экстр.

.

19. экстр.

.

20. экстр.

.

Варианты для выполнения четвертого задания

№ варианта	Координаты начальной точки
1	(0,5; 0,5)
2	(1; 0,2)
3	(-0,5; 0,7)
4	(-1,2; 1,5)
5	(-1,5; 0,5)
6	(-1,7; 1,9)
7	(-2; 1,5)
8	(-2,1; 1,1)
9	(-1,5; -0,5)
10	(-1,7; -1,2)
11	(-1,4; -1,4)
12	(-2,0; -1,2)
13	(1,2; -1,2)
14	(1,5; -1,5)
15 16 17 18 19 20	(-2; -1,4) (-2,3;2) (2,8;-1) (0,5;2,5) (-1,3;-1) (0,5;-1,4)

Пример Задание №1 графический метод решения задач линейного программирования

Графический метод применяется для решения задач небольшой размерности (количество переменных равно двум). Рассмотрим метод на примере решения следующей задачи:

Q = x₁ + x₂  max;

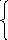x₁  10 ,

x₁ + 2x₂  20 , (2.3)

x₁ , x₂  0 .

Способ 1.

1. Заменяем ограничения неравенства ограничениями равенствами:

x₁ = 10 ,

x₁ + 2x₂ = 20 ,

x₁ = x₂ = 0.

2. Строим графики полученных функций:

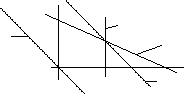Х₂

С

10 Х₁=10

Q = 0 область А

допустимых Х₁+2Х₂=20

решений

В

0 10

Q = max

Рис. 2.1. Графический метод решения ЗЛП.

3. Находим область допустимых решений (область, где выполняются все ограничения).

4. Строим график целевой функции при каком-либо значении правой части:

Q = x₁ + x₂ = 0 ,

x₂ = - x₁ .

5. График целевой функции перемещаем параллельно его начальному положению в сторону роста

(уменьшения при Q min) целевой функции до касания с границей области допустимых решений.

Граничная точка (или отрезок прямой) является решением задачи линейного программирования.

5. В ответе записываем координаты граничной точки (точка А) и значение целевой функции в этой точке:

А [10; 5], Q_max = 15.

Выводы: 1. область допустимых решений задачи линейного программирования представляет

собой выпуклый многогранник;

2. решение задачи линейного программирования находится на границе области

допустимых решений.

Способ 2.

1 - 3 пункты выполняются аналогично Способу 1.

4. Подсчитываем значения целевой функции во всех вершинах допустимого многогранника и выбираем экстремальное значение:

O [0; 0] , Q = 0 ;

C [0; 10] , Q = 10 ;

A [10; 5] , Q = 15 ;

B [10; 0] , Q = 10 .

Q_max = 15, следовательно, точкаA [10; 5]- решение задачи.

СИМПЛЕКС-МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Q = x₁ + x₂  max,

x₁  10 ,

x₁ +2 x₂  20 ,

x₁ , x₂  0 .

1. Приведем задачу к каноническому виду путем введения искусственных переменных:

x₁ + x₃ = 10

x₁ + 2x₂ + x₄ = 20

G = -x₁ - x₂  min.

2. Составляем симплекс-таблицу:

	1		2
3	1	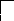0		10
4	1		2	20				разрешающая строка
	- 1		-1	0

разрешающий столбец

Так как имеются отрицательные коэффициенты целевой функции, то вершина, которой соответствует симплекс-таблица, не оптимальна. Максимальный по модулю отрицательный коэффициент ЦФ - (- 1), следовательно, любой столбец является разрешающим.

Для определения разрешающей стройки находим отношения правых частей ограничений к положительным коэффициентам разрешающего столбца и выбираем минимальное отношение:

10/0 = бесконечность

20/2 = 10

3. Составляем новую симплекс-таблицу:

Разрешающий элемент = 1.

Новый разрешающий элемент: 1:2 = 0,5.

Новая разрешающая строка: 10,5 = 0,5 ; 200,5 = 10.

Новый разрешающий столбец: 0(-0,5) = 0 ; (-1)(-0,5) = 0,5.

Элементы других столбцов:

1		0		1		10		0		10
-1	- 0,5 	-1	=	-0,5		0	- 10 	-1	=	10

Новая симплекс-таблица:

	1		4
3	1	0		10
2	0,5		0,5	10
	-0,5		0,5	10

разрешающая строка

разрешающий столбец

Так как имеются отрицательные коэффициенты целевой функции, то вершина, которой соответствует симплекс-таблица, не оптимальна. Максимальный по модулю отрицательный коэффициент ЦФ - (- 0,5), следовательно, первый столбец является разрешающим.

Для определения разрешающей стройки находим отношения правых частей ограничений к положительным коэффициентам разрешающего столбца и выбираем минимальное отношение:

10/1 = 10

10/0,5 = 20

Далее повторяется пункт №3.

Новая симплекс-таблица:

	3	4
1	1	0	10
2	-0,5	0,5	5
	0,5	0,5	15

Все коэффициенты целевой функции положительны, следовательно, найдено оптимальное и единственное решение задачи.

Ответ: координаты вершины (x₁ =10, x₂ = 5, x₃ = 0, x₄ = 0), G _min = -15, Q_max = 15.

Задание № 2

Найти минимум унимодальной функции