3.7. Циркуляция и поток вектора магнитной индукции

Циркуляция и поток вектора магнитной индукции (как и любого вектора вообще) определяются так же, как и для вектора напряженности электрического поля.

Циркуляцией по отрезку прямой однородного поля называется скалярное произведение:, где угол между векторами и.

Рассмотрим участок произвольной направленной кривой. Разобьем этот участок на мелкие отрезки, направленные так же, как и сама кривая. Тогда, циркуляцией векторапо участку кривойназывается криволинейный интеграл , который представляет собой предел суммы при делении кривой на бесконечно малые отрезки:

.

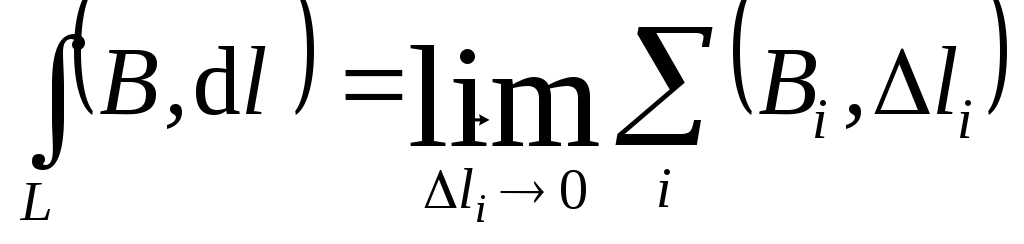Малый участок кривой можно считать прямым отрезком, а поле в пределах этого участка однородным, поэтому каждое слагаемое в сумме представляет собой циркуляцию векторапо отрезку.

Циркуляцию вектора позамкнутой кривой будем обозначать как .

Магнитным потоком вектора в однородном поле через плоскую поверхность площадиназывается величина

, (3.19)

где  единичный вектор нормали к поверхности,  угол между направлением вектора и направлением нормали к поверхности. В системе СИ единица измерения магнитного потокаВебер (Вб).

Теперь рассмотрим участок произвольной поверхности . Потоком векторачерез участок поверхностиназывается поверхностный интеграл, представляющий собой предел суммы при делении поверхности на кускибесконечно малых площадей:

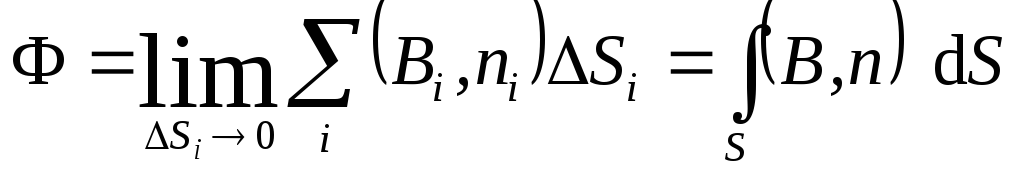. (3.19,а)

Малый участок поверхности можно считать плоским, а полев пределах этого участка – однородным, поэтому каждое слагаемое в суммепредставляет собой поток векторачерез плоскую поверхность.

Поток вектора череззамкнутую поверхность будем обозначать как .

Сформулируем две теоремы о циркуляции и потоке вектора магнитной индукции.

Теорема о циркуляции вектора магнитной индукции (для поля в вакууме). Циркуляция вектора магнитной индукции по произвольному замкнутому направленному контуру:

, (3.20)

где  алгебраическая сумма токов, пронизывающих произвольную поверхность, натянутую на контур, по которому вычисляется циркуляция. Направление обхода контура и направление нормали к натянутой на него поверхности связаны правилом буравчика. Если ток идет по направлению нормали, то его следует считать положительным, если наоборот – отрицательным.

Например, циркуляция вектора магнит­ной индукции по контуру , изображенному на рис. 3.14, равна.

Теорема о потоке вектора магнитной индукции. Поток вектора магнитной индукции через произвольную замкнутую поверхность равен нулю:

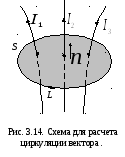
. (3.21)

Теоремы о циркуляции и потоке вектора магнитной индукции полезно сравнить с соответствующими теоремами для вектора напряженности электрического поля. Вспомним теорему о потоке вектора напряженности электрического поля (теорема Гаусса, см. формулу 1.18):

.

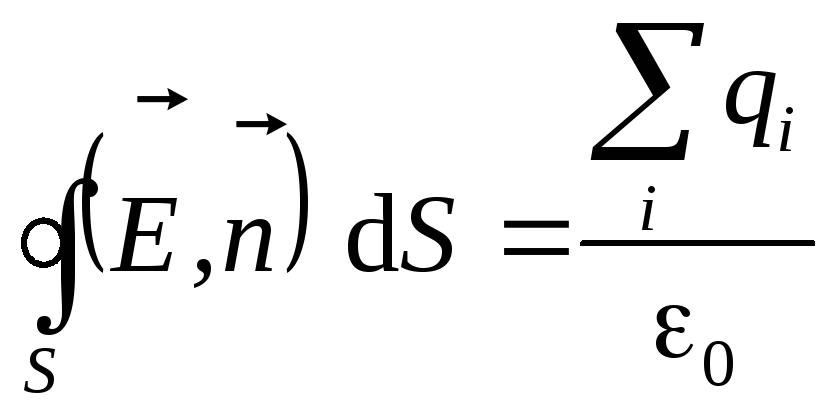Смысл этой теоремы в том, что источниками электрического поля являются электрические заряды. Они и создают поток вектора напряженности электрического поля. Силовые линии начинаются на зарядах и обрываются на них же. А смысл теоремы о потоке вектора магнитной индукции в том, что магнитных зарядов в природе не существует. Поэтому магнитные силовые линии нигде не начинаются и не заканчиваются, они замкнуты. Это и означает, что поток вектора магнитной индукции через любую замкнутую поверхность равен нулю (сколько линий войдет внутрь поверхности, столько и выйдет).

Циркуляция вектора напряженности электрического поля по любому замкнутому контуру равна нулю (уравнение 1.34):

.

Смысл этого уравнения в том, что электрическое поле, созданное любой системой зарядов, является полем потенциальным (подробнее см. п. 1.12). Электрическое поле, помимо напряженности  силовой характеристики, имеет еще и энергетическую характеристику – потенциал. Теорема о циркуляции для вектора магнитной индукции говорит о том, что источниками магнитного поля являются электрические токи (по сути, движущиеся электрические заряды), которые и создают циркуляцию вектора . Кроме того, поскольку циркуляция вектора магнитной индукции по замкнутому контуру может быть отлична от нуля, магнитное поле – поле непотенциальное. Поля с замкнутыми силовыми линиями называют вихревыми или соленоидальными. Таковым и является магнитное поле.

Приведем несколько примеров на применение теоремы о циркуляции для магнитного поля.

Пример 3.6. Определить магнитное поле, создаваемое прямым бесконечно длинным проводником с током .

Решение. В качестве произвольного замкнутого контура выберем окружность с радиусом, центр которой находится на оси провода (такой контур совпадет с одной из силовых линий – см. рис. 3.13, а). В данном случае скалярное произведение. Поскольку контур пронизывается всего одним током, по теореме о циркуляции для магнитного поля получаем:

.

Величина вектора одинакова во всех точках контура, следовательно, её, как постоянную, можно вынести за знак интеграла:

.

Интеграл представляет собой просто длину контура. Таким образом,

,

откуда находим величину магнитного поля на расстоянии от провода:

.

Последнее выражение в точности совпадает с результатом, полученным в примере 3.3 (см. формулу 3.14) из закона Био-Савара-Лапласа.

Отметим, что формулой 3.14 можно пользоваться и в случае проводника конечных размеров при расчете поля приблизительно напротив центральной части проводника в точках, отстоящих от него на расстояниях, гораздо меньших длины проводника.

Пример 3.7. Найти магнитное поле внутри соленоида длиной , с числом виткови током.

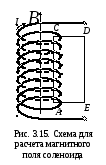
Решение. В качестве контура обхода выберем прямоугольный контур АСDЕ (см. рис. 3.15) так, что отрезок АС приблизительно лежит в средней части соленоида, а отрезок DЕ удален на большое расстояние от соленоида. По теореме о циркуляции для магнитного поля имеем:

.

Помещая небольшую магнитную стрелку в различные точки пространства, можно показать, что магнитное поле в средней части соленоида как снаружи, так и внутри, направлено параллельно оси соленоида. Следовательно, на отрезках контура СD и ЕA скалярное произведение

,

а на отрезке АС:

.

Таким образом, циркуляции магнитного поля по отрезкам CD и ЕA равны нулю:

, ,

а по отрезку АС:

(здесь величина вектора магнитной индукции вынесена за знак интеграла, поскольку она должна быть постоянна на отрезке АС из-за осевой симметрии системы). На большом расстоянии от соленоида величина магнитной индукции близка к нулю, поэтому и циркуляция магнитного поля по отрезку DЕ равна нулю:

.

В итоге получим:

Сумма токов, пронизывающих контур ACDE:

,

где  число витков, пронизывающих контур ACDE (на рис. 3.15 эти витки показаны),  число витков, приходящееся на единицу длины соленоида. Тогда:

.

Если число витков на единицу длины соленоида представить как , где общее число витков, а  длина соленоида, то:

.

Полученный результат совпадает с формулой (3.18) для поля на оси бесконечно длинного соленоида. Пользуясь теоремой о циркуляции, мы показали, что в случае достаточно длинного соленоида результат (3.18) можно использовать и для расчета поля в любой точке внутри соленоида в средней его части, а не только на оси.