Тогда:
dW = µbV 
 2g
2g 
 H −Vt2 tdt .
H −Vt2 tdt .
Полный объем за время открытия щита:
W = ∫dW = ∫µbV 2g |
|
H −Vt |
tdt . |
W |
T |
|
2 |
|
0 |
0 |
|
|
Для решения интеграла введем подстановку:
H |
Vt |
y; t |
2 |
(H y); |
dt |
2 |
dy. |
|
2 |
|
V |
|
V |
При этом пределы переменной y будут от H до H − a2.
|
|
|
|
|
|
|
|
|
|
H − |
a |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
W = −µbV |
|
|
|
2 y1/ 2 |
|
(H − y) |
|
dy . |
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
2g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
V |
|
|
|
V |
|
|
|
|
|
Решение интеграла дает: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
5 |
|
8µb 2g |
1 |
|
|
|
a |
|
H |
|
|
a |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
W = |
|
|
|
|
|
H |
− |
|
|
|
− |
|
|
|
H − |
|
|
|
|
+ |
|
H |
|
. |
V |
|
|
|
2 |
3 |
|
|
|
|
15 |
|
|
|
|
|
5 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя числовые значения в решение, получим объем
W = 153 м3.
Ответ: W = 153 м3.
4.1.1. Задачи к разделу. Истечение жидкости при постоянном
и переменном напоре
Задача 4-1. Определить суммарный расход воды Q1 из резервуара через два отверстия в его стенке: круг
лое диаметром |
d, |
расположенное |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на расстоянии е от дна и квадратное со |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стороной а, примыкающее одной сто- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
роной к дну. Глубина воды в резерву- |
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
аре h. Каков будет суммарный расход |
|
|
|
|
e |
|
|
|
|
|
|
|
Q2,есликверхнемуотверстиюприсое |
|
|
|
|
|
|
|
|
|
a |
|
|
динить цилиндрический насадок. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Параметр |
|
|
|
|
Вариант |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
3 |
|
4 |
|
|
5 |
|
6 |
|
|
|
|
|
|
|
d, cм |
4 |
|
5 |
|
5,5 |
|
4,2 |
|
|
4,6 |
|
5,2 |
е, см |
100 |
|
110 |
|
120 |
|
130 |
|
140 |
|
150 |
а, см |
8 |
|
9 |
|
11 |
|
10 |
|
|
7 |
|
8 |
h, см |
200 |
|
240 |
|
260 |
|
280 |
|
300 |
|
320 |
Задача 4-2. В теле железобетонной плотины имеется во- |
доспуск в виде трубы длиной l. Напор над водоспуском при |
свободном истечении Н |
1. Разность отметок ВБ и НБ состав- |
ляет Н2. Скорость подхода воды |
|
|
|
|
|
к плотине V0. Определить диа- |
|
H1 |
l |
|
H2 |
метр водоспуска, если расход |
V0 |
|
|
Q=12 м3/с. Установить какой |
|
|
|
|
расход будет через водоспуск, |
|
|
|
|
|
если уровень |
нижнего |
бьефа |
|
|
|
|
|
поднимется на h=10 м. |
|
|
|
|
|
|
Параметр |
|
|
Вариант |
|
|
1 |
2 |
3 |
|
4 |
5 |
6 |
l, м |
|
5 |
5,2 |
5,4 |
|
5,6 |
5,8 |
6 |
H1, м |
6,5 |
7 |
7,5 |
|
8 |
8,5 |
9 |
H2, м |
15 |
15,5 |
16 |
|
16,5 |
17 |
17,5 |
V0, м/с |
0,4 |
0,45 |
0,5 |
|
0,42 |
0,44 |
0,46 |
|
|
291 |
|
|
|
|
|
Задача 4-3. Вода вытекает из открытого бака через цилиндрический насадок диаметром d при постоянном напоре Н в атмосферу. Сосуд ёмкостью W, подставленный под струю, наполнился за Т секунд. Определить коэффициент потерь насадка и потери напора в насадке.
|
Параметр |
|
|
Вариант |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
d, мм |
15 |
18 |
20 |
22 |
20 |
22 |
|
H, м |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
|
W, л |
20 |
23 |
25 |
27 |
25 |
27 |
|
T, сек |
31 |
33 |
35 |
40 |
42 |
25 |
Задача 4-4. Отверстие в виде равностороннего треугольника со стороной «а» перекрыто щитом. Щит поднимается равномерно со скоростью V. Определить объём воды, вытекающей за время Т полного открытия отверстия. Напор перед щитом отверстия – Н1=const. Истечение свободное. Коэффициент расхода отверстия – μ = 0,58 = const.
|
Параметр |
|
|
Вариант |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
a, м |
1 |
1,2 |
1,4 |
1,6 |
1,8 |
2 |
|
V, см/с |
2,5 |
2,8 |
3 |
3,2 |
3,4 |
3,6 |
|
T, сек |
34,6 |
37,12 |
40,4 |
43,3 |
45,85 |
48,11 |
|
H1, м |
3,5 |
4 |
4,5 |
5 |
5,5 |
6 |
Задача 4-5. Насос подаёт воду в резервуар в количестве Q0. Высота резервуара h, диаметр – D. В дне имеется круг лое отверстие диаметром d, через которое вода вытекает в атмосферу. Определить, в течение какого времени насос

должен подавать воду в резервуар, чтобы наполнить его до краёв, если в начальный момент времени глубина воды в резервуаре равна Н1.
|
Пара- |
1 |
2 |
Вариант |
5 |
6 |
Q0 |
|
|
метр |
3 |
4 |
|
|
|
Q0, л/с |
6 |
6,5 |
7 |
7,5 |
8 |
8,5 |
D |
h |
|
h, м |
1,4 |
1,6 |
2 |
2,4 |
2,8 |
3,2 |
|
|
|
|
D, м |
1,26 |
1,3 |
1,4 |
1,45 |
1,5 |
1,6 |
|
H1 |
|
d, см |
4 |
4,2 |
4,6 |
4,8 |
5 |
5,2 |
|
|
H1, см |
30 |
20 |
35 |
40 |
45 |
50 |
|
|
Задача 4-6. На поршень диаметром D действует сила F. Определить скорость движения поршня при диаметре отверстия в поршне d и толщине поршня а.
|
Пара- |
|
|
Вариант |
|
|
D |
|
|
|
|
|
|
|
метр |
1 |
2 |
3 |
4 |
5 |
6 |
P |
|
D, мм |
100 |
120 |
130 |
140 |
160 |
200 |
F |
|
a |
|
F, кН |
1 |
1,2 |
1,6 |
2 |
2,4 |
2,8 |
|
d, мм |
2 |
2,2 |
2,6 |
2,8 |
3 |
3,2 |
d |
|
a, мм |
8 |
10 |
12 |
8 |
10 |
12 |
|
Задача 4-7. Вертикальный цилиндрический бак имеет размеры: высоту h и радиус поперечного сечения r. В дне бака сделано отверстие диаметром d. Глубина воды в баке – Н. Определить объём воды в баке через Т минут после открытия отверстия, если постоянный приток воды в бак – Q0.
|
Параметр |
|
|
Вариант |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
h, м |
2,8 |
3 |
3,2 |
3,4 |
3,6 |
4 |
|
r, м |
1 |
1,2 |
1,4 |
1,6 |
1,2 |
1,4 |
|
d, см |
2,5 |
2,6 |
2,7 |
2,4 |
2,8 |
3 |
|
H, м |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
2 |
|
Т, мин |
15 |
10 |
12 |
18 |
20 |
14 |
|
Q0, л/с |
1,2 |
1 |
0,8 |
1,6 |
1,8 |
2 |
|
|
|
|
|
|
|
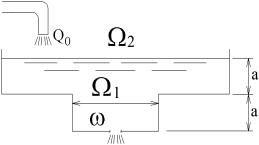
Задача 4-8. Посто- |
янный приток |
воды |
в |
резервуар |
составля- |
ет Q0. В дне резервуа- |
ра |
сделано отверстие |
ω. |
Площадь |
нижней |
части |
резервуара |
– |
Ω1, |
верхней |
– |
Ω2. |
К моменту открытия отверстия глубина воды над отверстием
равнялась 2а. Через какое время после открытия отверстия глубина воды над ним будет равна а/2.
|
Параметр |
|
|
Вариант |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
Q0, л/с |
2 |
2,2 |
2,4 |
2,5 |
3 |
3,5 |
|
ω, см2 |
15 |
17 |
19 |
22 |
24 |
26 |
|
Ω1, м2 |
2 |
2,2 |
2,5 |
2,7 |
3 |
3,2 |
|
Ω2, м2 |
4 |
4,4 |
4,8 |
5,2 |
5,6 |
6 |
|
a, м |
0,9 |
1,2 |
1,3 |
1,4 |
1,5 |
1,6 |
Задача 4-9. Из цилиндрического бака с площадью поперечного сечения Ω вытекает вода через отверстие диаметром d в дне. Через 30 минут после открытия отверстия глубина в баке оказалась равной h. Сколько литров воды вытекло за первые Т минут?
|
Параметр |
|
|
Вариант |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
Ω, м2 |
0,95 |
1,7 |
1,4 |
1,6 |
1,8 |
2 |
|
d, см |
2 |
2,1 |
2,2 |
2 |
2,1 |
2,2 |
|
h, см |
25 |
20 |
21 |
22 |
23 |
26 |
|
Т, мин |
10 |
8 |
7 |
6 |
5 |
4 |
Задача 4-10. Определить время опорожнения цилиндрического сосуда, имеющего площадь поперечного сечения Ω, глубину воды h в трёх случаях истечения:
1) через круглое отверстие |
|
|
|
Ω |
|
|
|
|
|
|
|
|
|
|
Ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ω |
|
|
диаметром d в дне сосуда; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
2) через вертикальный |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
цилиндрический |
насадок |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lн |
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
диаметром d и длиной lн, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
присоединённый |
к отвер- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стию в дне; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3)черезвертикальнуютрубудиаметромd,длинойl,присое динённую также как и насадок. Коэффициент расхода системы в этом случае принять μ = 0,7.
|
Параметр |
|
|
Вариант |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
Ω, м2 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
|
h, м |
1,8 |
2 |
2,2 |
2,4 |
2,6 |
2,2 |
|
d, см |
5 |
5,2 |
5,4 |
5,6 |
5,2 |
5,4 |
|
lн, см |
20 |
21 |
22 |
23 |
24 |
20 |
|
l, см |
310 |
320 |
310 |
330 |
320 |
310 |
Задача 4-11. Из закрытого резервуара в атмосферу вытекает вода через круглое отверстие диаметром d в тонкой стен-
ке |
и |
внешний |
цилиндрический |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
насадок диаметром d. Опреде- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лить манометрическое давление |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рм |
на |
свободной поверхности |
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
воды в резервуаре, если разность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
расходов отверстия и насадка |
Q, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а напор над центром отверстия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и насадка – Н. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Параметр |
|
|
|
|
|
Вариант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
3 |
|
4 |
|
|
5 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d, мм |
|
20 |
22 |
|
18 |
|
24 |
|
16 |
|
|
26 |
|
|
|
Q, л/с |
|
0,7 |
0,9 |
|
0,5 |
|
1,2 |
|
0,3 |
|
|
1,4 |
|
|
|
Н, м |
|
1,5 |
2 |
|
2,2 |
|
2,4 |
|
2,6 |
|
|
3 |
|
Задача 4-12. Определить расход и давление в отверстии плотины при заданных d, l=4d и Н.
Пара- |
|
|
Вариант |
|
|
метр |
1 |
2 |
3 |
4 |
5 |
6 |
d, м |
0,5 |
0,7 |
0,9 |
1,2 |
1,5 |
1,1 |
Н, м |
8 |
10 |
12 |
14 |
16 |
13 |
|
Задача 4-13. Из водохранилища вода вытекает через от- |
|
верстие в плотине диаметром d. Определить время, за кото- |
|
рое уровень воды в водохранилище |
|
|
|
опустится |
на h, если начальный на- |
H |
l |
|
пор Н, а толщина плотин l, при ус- |
d |
|
|
|
ловии, что площадь зеркала воды |
|
|
|
в водохранилище Ω не изменяется |
|
|
|
с изменением уровня. |
|
|
|
Параметр |
|
|
Вариант |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
d, м |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
h, м |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
Н, м |
6,5 |
7,5 |
8,5 |
9,5 |
10,5 |
11 |
|
l, м |
2 |
2,2 |
2,4 |
2,6 |
2,8 |
3 |
|
Ω, км2 |
0,224 |
0,25 |
0,3 |
0,325 |
0,35 |
0,375 |
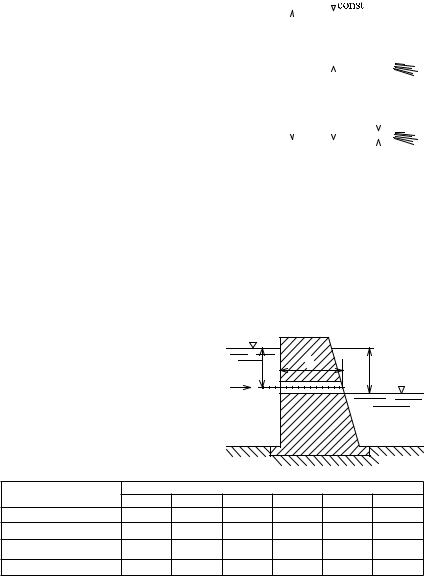
Задача 4-14. Бак с квадратным основанием а × а и высотой Н заполнен доверху водой. Найти время, за которое из бака вытечет половина воды через внешний цилиндрический насадок диаметром d в дне бака.
|
Параметр |
|
|
Вариант |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
а, м |
1 |
1,2 |
1,4 |
1,6 |
1,8 |
2 |
|
Н, м |
2 |
2,5 |
2,8 |
3,4 |
3,6 |
4 |
|
d, мм |
40 |
42 |
44 |
46 |
48 |
50 |

|
Задача 4-15. Призмати- |
|
|
ческий бак с прямоугольным |
|
|
основанием a × b разделён |
|
|
пополам |
перегородкой |
на |
H |
|
два отсека, в которой име- |
|
|
|
ется отверстие с цилиндри- |
|
|
ческим насадком диаметром |
l1 |
|
d. Высота бака Н, глубина |
|
|
воды в левом отсеке Н1 поддерживается постоянной; насадок |
|
расположен на высоте l1 |
от дна. Принимая, что в начальный |
|
момент правый отсек пуст, определить время его наполнения. |
|
Параметр |
|
|
Вариант |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
a, м |
1 |
1,2 |
1,4 |
1,6 |
1,8 |
2 |
|
b, м |
2 |
2,2 |
2,4 |
2,6 |
2,8 |
3 |
|
d, мм |
50 |
55 |
60 |
65 |
70 |
65 |
|
Н, м |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
|
Н1, м |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
|
l1, м |
0,2 |
0,22 |
0,24 |
0,26 |
0,28 |
0,3 |
Задача 4-16. В баке, имеющем в дне отверстие диаметром d1, а в стенке – отверстие, снабженное цилиндрическим насадком диаметром d2, установился уровень воды на высоте Н. Определить, каков расход воды Q, поступающей в бак, если центр бокового отверстия возвышается над дном бака на высоту h. Определить скорости истечения из отверстия V1 и насадка V2.
|
Параметр |
|
|
Вариант |
|
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
d1, мм |
120 |
100 |
140 |
120 |
80 |
|
d2, мм |
80 |
90 |
70 |
80 |
60 |
|
H, м |
2,6 |
2,8 |
1,8 |
1,4 |
2,0 |
|
h, м |
0,4 |
0,3 |
0,4 |
0,3 |
0,4 |
d2 |
H |
h |
d1 |
Рисунок к задачам 4-16…4-17 |
Задача 4-17. В бак, имеющий в дне отверстие диаметром d1, а в стенке отверстие, снабженное цилиндрическим насадком диаметром d2, поступает вода расходом Q. Определить уровень воды Н, если центр бокового отверстия возвышается над дном бака на высоте h.
|
Параметр |
|
|
Вариант |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
d1, мм |
160 |
80 |
130 |
120 |
85 |
|
d2, мм |
80 |
75 |
100 |
100 |
60 |
|
Q, дм3/с |
6,0 |
4,5 |
7,6 |
5,6 |
7,0 |
|
h, м |
0,4 |
0,3 |
0,4 |
0,3 |
0,4 |
|
|
|
|
|
|
|
Задача 4-18. В бак, разделенный тонкой перегородкой на два отсека, поступает вода. В перегородке имеется отверстие диаметром d1. Из второго отсека вода сливается наружу через конический насадок диаметром d2. При напоре Н1 определить расход Q.
|
Параметр |
|
|
Вариант |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
Н1, м |
98 |
86 |
178 |
120 |
160 |
|
d1, мм |
80 |
70 |
90 |
75 |
80 |
|
d2, мм |
75 |
75 |
50 |
50 |
75 |
|
|
|
298 |
|
|
|
рa |
рa |
|
|
|
H1 |
H 2 |
d2 |
d1 |
|
|
Рисунок к задачам 4-18…4-19 |
|
Задача 4-19. В бак, разделенный тонкой перегородкой на два отсека, поступает вода расходом Q. В перегородке имеется отверстие диаметром d1. Из второго отсека вода сливается наружу через конический насадок диаметром d2. Зная напор Н1, определить диаметр d2.
|
Параметр |
|
|
Вариант |
|
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
Q, дм3/с |
30 |
26 |
28 |
26 |
32 |
|
d1, мм |
90 |
85 |
98 |
80 |
100 |
|
Н1, м |
7,5 |
6 |
10 |
12 |
11 |
Задача 4-20. В бак, разделенный тонкой перегородкой на два отсека, поступает вода расходом Q. В дне каждого отсека имеются одинаковые отверстия диаметром d1 = d2, а в перегородке – отверстие диаметром d3. Определить напоры Н1 и Н2.
|
Параметр |
|
|
Вариант |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
Q, дм3/с |
30 |
32 |
34 |
36 |
38 |
|
d1 = d2, мм |
100 |
100 |
100 |
150 |
125 |
|
d3, мм |
150 |
125 |
100 |
150 |
100 |











 2g
2g 
 H
H