
ГиТ35
.pdf
Решение. Находим скорость воздуха в трубе:
V |
Q |
0,078 |
4 |
|
|
10 м/с. |
||
|
3,14 |
|
2 |
|
|
|||
|
|
0,1 |
|
|
|
|||
Число Рейнольдса |
для |
|
потока |
воздуха в трубе при |
||||
v = 15,7.10-6 м2/с (табл. П-8): |
|
|
|
|
|
|||
Re |
V d |
|
10 |
0,1 |
|
69000. |
||
|
15,7 |
10 6 |
||||||
|
|
|
||||||
Относительная шероховатость (по табл. П-15 kЭ = 0,2 мм):
kЭ /d = 0,2/100 = 0,002.
Коэффициент гидравлического трения:
λ = 0,11.(kЭ /d + 68/Re)0?25 = 0,11.(0,00+0,001)0,25=0,0256.
По формуле Дарси-Вейсбаха находим потери давления на трение (ρ = 1,18 кг/м3):
pЛ |
l |
V 2 |
0,0256 |
100 |
1,18 |
102 |
|
d |
2 |
0,1 |
2 |
||||
|
|
|
|||||
|
|
1410Па |
1,41 кПА. |
|
|
||
Ответ: р = 1,41 кПа.
Пример 3.5. Расход воды при температуре 10˚ C в горизонтальнойтрубекольцевогосечения,состоящейиздвухконцент рических оцинкованных стальных труб (при kЭ = 0,15 мм),
180

Q = 0,75 м3/с. Внутренняя труба имеет наружный диаметр d=0,075м,анаружнаятрубаимеетвнутреннийдиаметрD =0,1м. Найти потери напора на трение на длине трубы l=300 м.
Решение. Площадь живого сечения:
ω = π4 (0,12 −0,0752 )= 0,0034 м2.
Смоченный периметр живого сечения:
χ = π.(0,075+0,1) = 3,14.0,175 = 0,55 м.
Эквивалентный диаметр:
dЭ = 4.R = 4 ω/χ = 4.0,0034/0,5 = 2,48.10-2 м.
Относительная шероховатость:
Э |
1,5 10 4 |
0,0059. |
|
dЭ |
|
2,48 10 2 |
|
Средняя скорость течения:
V = Q/ω = 0,0075/0,0034 = 2,2 м/с.
Число Рейнольдса при v = 1,31.10-6 м2/с (см. табл. П-12):
Re |
V dЭ |
2,2 2,5 10 |
2 |
42000. |
|
1,31 10 6 |
|
||
|
|
|
|
Коэффициент гидравлического трения:
 0,11
0,11 ( Э
( Э  dЭ 68
dЭ 68 Re) 0,25
Re) 0,25 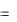
 0,11
0,11 (0,0059 68
(0,0059 68 42000) 0,25
42000) 0,25  0,0284.
0,0284.
181

Потери напора на трение по длине находим по формуле Дарси-Вейсбаха:
hЛ |
l |
|
V 2 |
0,0284 |
300 2,2 |
2 |
84 |
м. |
|
dЭ |
|
2 g |
2,48 10 2 |
2 9,8 |
|||||
|
|
|
|
|
|||||
Ответ: hЛ = 84 м.
Пример 3.6. Определить расходы воды в трубе прямоугольного поперечного сечения с отношением сторон a:b=0,25
ив круглой трубе при той же площади поперечного сечения ω = 2.10-4 м2, если потери давления в этих трубах одинаковы
иравны ∆ρЛ=100 Па, а длина каждой трубы l=10 м. Температура воды 20˚ C.
Решение. Для трубы круглого сечения dЭ = d; для трубы прямоугольного сечения при a:b =0,25:
d |
Э |
4 а b |
2 a b |
1,6а. |
|
2 (a b) |
a b |
||||
|
|
Найдём эквивалентные диаметры для этих труб:
|
|
|
|
|
|
|
|
|
dЭ.КР |
4 |
|
|
|
4 2 10 4 3,14 1,6 10 2 м; |
|||
|
|
|
|
|
|
|||
dЭ.ПР 1,6 |
|
|
1,6 2 10 4 4 1,1 10 2 м. |
|||||
|
4 |
|||||||
Потери давления определяем по формуле Дарси-Вейсбаха. Предположим первоначально, что режим течения в трубах ламинарный. Тогда по формуле λ=A/Re, где значение коэффициента формы А (см. табл. П-24) для круглых труб равно 64, для прямоугольных – 73, найдем коэффициент Дарси.
182

Формула потерь давления принимает вид:
p |
|
А |
|
l |
V 2 А l |
V 2 |
Аl |
V . |
|||
|
|
|
|
|
|
|
|
|
|
||
Л Re |
|
dЭ |
2 VdЭ dЭ |
2 |
2dЭ2 |
||||||
|
|
|
|||||||||
Для круглой трубы при плотности воды p = 998,2 кг/м3 (см. табл. П-4) и вязкости v ≈ 10-6 м2/с (см. табл. П-12):
V |
2 |
pЛ dЭ |
2 |
2 100 (1,6 10 2) 2 |
0,08 м/с; |
|
Аl |
|
998,2 64 10 10 6 |
для прямоугольной трубы:
|
2 100 (1,1 10 |
2 |
2 |
|
|
V |
) |
|
0,03 м/с. |
||
998,2 73 10 10 6 |
|||||
|
|
||||
Определяем числа Рейнольдса:
•для круглой трубы:
Re =VdЭ = 0,08.1,6.10-2/10-6=1280;
•для прямоугольной трубы:
Re = 0,032.1,1.10-2/10-6 = 350.
Поскольку числа Рейнольдса меньше критического, равного 2320,режимтечениявтрубах,какипредполагалось,ламинарный.
Расход воды:
•в круглой трубе:
Qкр = Vω = 0,08.2.10-4 = 1,6.10-5 м3/с;
183

•в прямоугольной трубе:
Qпр=0,03.10-4 = 0,64.10-5 м3/с.
Таким образом, в условиях ламинарного движения при одной и той же площади живого сечения и одинаковых потерях давления круглая труба пропускает расход в 2,5 раза больший, чем труба прямоугольного сечения.
Ответ: Qкр = 1,6.10-5 м3/с; Qпр= 0,64.10-5 м3/с.
Пример 3.7. Определить диаметр d нового стального трубопровода длиной l =1000 м, который должен пропускать расход воды Q= 0,02 м3/с, при потерях давления ∆рЛ = 2.105 Па. Температура подаваемой воды 20˚C.
Решение. Предполагаем, что трубопровод работает в квадратичной области сопротивления, тогда найдем коэффициент Дарси по формуле Шифринсона:
|
|
0,25 |
|
0,11 |
Э |
, |
|
d |
|||
|
|
где кЭ = 5.10-5 м (см. табл. П-15).
НайдемсреднююскоростьтеченияпоформулеДарси-Вейсбаха:
V |
2 pЛ d |
. |
|
l |
|
Подставляявэтовыражениеформулудляλиучитывая,чторасход:
Q =Vω =V π d 2 4,
4,
184

получим:
Q |
d 2 |
|
2 |
|
p |
Л |
d1,25 |
|
|
0,785 |
|
2 p |
Л |
|
|
|
d 2,5 . |
|||
4 |
0,11 |
kЭ |
0,25 |
l |
|
|
0,11 kЭ |
0,25 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
Для условий задачи при р = 998,2 кг/м3(см. табл. П-4): |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
0,02 |
0,785 |
|
|
|
2 |
2 105 |
|
|
|
|
d |
2,5 |
; |
||||||
|
0,11 |
(5 10 |
5 |
0,25 |
998,2 1000 |
|
|
|
|
|
||||||||||
|
|
|
|
) |
|
|
|
|
|
|
|
|
||||||||
d=0,15м.
Площадь поперечного сечения трубы составит:

 d 2
d 2 4
4 0,785
0,785 0,152
0,152  0,0176 м.
0,0176 м.
Скорость в трубопроводе равна:
V = Q/ω = 0,02/0,0176 = 1,13 м/с.
Число Рейнольдса при v = 10-6 м2/с (см. табл. П-12)
Re = V.D/v = 1,13.0,15/10-6 = 3,3.10-4.
При относительной шероховатости:
kЭ/d = 5.10-5/0,15=3,3.10-4;
и числе Рейнольдса Re = 1,17.105, согласно рисунку 3.1, находим,чтотрубопроводработаетвзонепереходногосопротивления.
185

Значения λ определяем по формуле Альтшуля:
0,11 |
kЭ |
68 |
0,25 |
0,11 |
5 10 5 |
68 |
|
|
|
0,25 |
||||
|
|
|
|
|
|
|
|
|
|
|
0,019. |
|||
d |
Re |
|
0,15 |
1,17 10 |
5 |
|||||||||
|
|
|
|
|
||||||||||
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 0,15 2 105 |
|
|
|
|
|||
V |
2 |
pЛ d |
|
|
|
1,75 м/с; |
||||||||
|
|
|
|
l |
0,019 1000 |
998,2 |
|
|
|
|||||
ω = Q/V = 0,02/1,75 = 0,0114 м2;
d=0,12 м.
Проверка показала, что при d=0,12 м и скорости 1,75 м/с трубопровод работает в зоне переходного сопротивления.
Уточним значение λ:
Re Vd 1,75
1,75 0,12
0,12 10 6
10 6  2,1
2,1 105 ;
105 ;
|
|
kЭ |
d 5 10 5 |
0,12 |
41,6 10 5; |
|
|
|||||
0,11 |
kЭ |
68 |
0,25 |
|
|
|
|
5 |
68 |
|
0,25 |
|
|
|
|
0,11 |
|
41,6 10 |
|
|
|
0,018 . |
|||
d |
Re |
|
2,1 10 |
5 |
||||||||
|
|
|
|
|
|
|
|
|||||
При λ=0,018: |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 105 |
0,15 |
|
|
|
|
V |
2 |
pЛ d |
|
1,8; |
|||||||
|
|
|
l |
0,018 1000 |
998,2 |
|
||||||
ω = Q/V =0,02/1,8 = 0,0111 м2; d = 0,118 м.
Ответ: d =0,118м.
186

Пример 3.8. Определить расход воды в бывшей в эксплуатации водопроводной трубе диаметром d=0,3 м, если скорость на оси трубы, замеренная трубкой Пито-Прандтля uМАКС = 4,5 м/с, а температура воды 10˚ C.
Решение. Находим по табл. П-15 значение абсолютной шероховатости для старых стальных труб: kЭ = 0,5 мм.
Предполагая, что движение воды происходит в квадратичной области турбулентного движения, определяем коэффициент гидравлического трения по формуле Шифринсона:
λ = 0,1.(kЭ/d)0,25 = 0,11.(0,5/300)0,25=0,022.
Среднюю скорость определяем по уравнению:
uМАКС V 1 |
1,35 |
|
|
1 1,35 |
0,022 |
1,2; |
V |
0,83 uМАКС |
3,74м с . |
||||
Кинематическая вязкость воды v = 1,13.10-6 м2/с = =0,0131 см2/с (см. табл. П-12).
Определяем значение критерия зоны турбулентности по формуле:
V  kЭ 374
kЭ 374 0,05 1430 500 . 0,0131
0,05 1430 500 . 0,0131
Таким образом, движение действительно происходит в квадратичной области сопротивления.
Расход воды в трубе находим из выражения:
Q 
 V
V 
 4d 2
4d 2  3,74
3,74  0,26 м3/с.
0,26 м3/с.
Ответ: Q = 0,26 м3/с.
187

Пример 3.9. Для ограничения расхода воды в водопроводной линии установлена диафрагма. Избыточные давления в трубе до и после диафрагмы постоянны и равны соответственно р 1 = 6,37.104 Па и р 2 = 2,05.104 Па. Диаметр трубы D = 0,076 м. Определить необходимый диаметр отверстия диафрагмы d с таким расчётом, чтобы расход в линии был ра-
вен Q = 0,0059 м3/с.
Решение. Потеря напора в диафрагме:
h |
p |
p |
|
6,37 104 |
2,05 10 |
4 |
||||||||||
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
4,4 м. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
g |
|
|
|
|
|
|
998,2 |
9,8 |
|
|
||||
Скорость воды в трубопроводе: |
|
|
|
|
|
|||||||||||
|
V |
4 Q |
|
|
4 0,0059 |
|
1,28 м/с. |
|||||||||
|
|
|
d 2 3,14 0,0762 |
|||||||||||||
|
|
|
|
|
|
|
||||||||||
Из формулы Вейсбаха: |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
h |
= |
ζ |
V 2 |
|
|
|
|
|||
|
|
|
|
|
|
2 |
g |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ДИАФР |
|
2 g |
h |
2 9,8 |
4,4 |
|
52,3. |
||||||||
|
|
|
V2 |
|
|
|
1,282 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Этому значению коэффициента сопротивления ζДИАФР соответствует отношение площадей сечения n = d2/D2, которое можно определить из следующей формулы:
ДИАФР n1 1 2 52,3,
188


 0,57
0,57 


 0,076
0,076

 0,205
0,205  0,0345 м.
0,0345 м.