
sopromat_uchebnik
.pdf
Схема 33. Раскрытие статической неопределимости
Рассматриваем равновесие |
Метод сечений |
|
системы |
||
|
||
Составляем уравнения равновесия |
||
Изображаем систему в |
Находим геометрические со- |
отношения между деформа- |
|
деформированном |
циями элементов системы |
состоянии |
(геометрические уравнения |
|
совместности деформаций) |
Закон Гука |
Выражаем деформации |
|
через усилия |
Физические уравнения совместности деформаций |
РЕШАЯ СОВМЕСТНО УРАВНЕНИЯ РАВНОВЕСИЯ И СОВМЕСТНОСТИ ДЕФОРМАЦИЙ, НАХОДИМ НЕИЗВЕСТНЫЕ СИЛЫ
61

Схема 34. Свойства статически определимых и статически неопределимых конструкций
Распределение усилий между |
элементами не зависит от их |
жесткости |
Усилия и напряжения в эле- |
ментах возникают только при |
наличии внешней нагрузки |
Изменение температуры не |
приводит к появлению усилий |
и напряжений |
Невозможно появление монтаж- |
ных напряжений |
Возможно проектирование кон- |
струкций с равно напряженными |
элементами |
62 |
Распределение усилий между |
элементами зависит от жестко- |
сти этих элементов. Изменяя |
соотношение жесткостей эле- |
ментов конструкций, можно |
любым образом менять распре- |
деление усилий в них |
При изменении температуры |
элементов возникают усилия и |
напряжения |
усилия и |
Могутсуществовать уси- |
напряжения при отсутствии |
лия и напряжения при от- |
внешней нагрузки (монтажные) |
сутствии внешней нагруз- |
ки (монтажные). |
Нельзя спроектировать конст- |
рукции с равнонапряженными |
элементами |

Схема 35. Методы расчета на прочность. Расчет на прочность по допускаемым напряжениям
Методы расчета на прочность при статических нагрузках
|
|
По допускаемым |
|
По предельным |
|
По допускаемым |
|
|
|||||
|
|
напряжениям |
|
состояниям |
|
|
нагрузкам |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используется в машиностроении |
|
|
Используется в строительстве |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Исходят из предположений |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В материале детали возникают |
|
Разрушение хрупкое или пластичное |
|
||||||||
|
|
только упругие деформации |
|
возникает в точке, где напряжение |
|
||||||||
|
|
|
|
|
|
|
|
достигает опасной величины |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Опасное напряжение σоп, τоп
Для хрупких материалов – предел |
|
Для пластичных материалов – |
прочности σu |
|
предел текучести σу |
|
|
|
Условие надежной работы
Реальной детали
Рабочее напряжение в детали должно быть много меньше опасного
σ p σоп , τ p τоп
Расчетной схемы детали
Расчетное напряжение должно быть много меньше опасного
Допускаемое напряжение σadm = σkоп , τadm = τопk
Условие прочности
Максимальное расчетное напряжение в опасной точке не должно превышать допускаемого σmax ≤ σadm , τmax≤τadm
63

Схема 36. Условие прочности при растяжении. Виды расчетов
Максимальноерасчет-
четноенапряжение
напряжение
Действуетпоперечномв- сечениином сечениистержнястержня
σmax = AN ,
где N - продольнаясилавопасномсечении; А- площадьпоперечногосечениястержня
УСЛОВИЕ ПРОЧНОСТИ
σMAX = AN ≤σadm ,
где σadm - допускаемое нормальное напряжение
Проектировочный
расчет
Определяется площадь поперечного сече-
ния
А≥ σNadm
Проверочный
расчет
Определяется
максимальное нормальное напряжение и сравнивается с
допускаемым
σmax ≤σadm
Определение допускаемой нагрузки (эксплуатацион-
ный расчет)
Nadm ≤σadmA
После изучения модуля «Растяжение, сжатие» студент должен знать и уметь все, что указано на схеме 37.
64

Схема 37. Результаты изучения модуля «Растяжение, сжатие»
Знать |
|
Уметь |
|
|
|
Определение деформации растяжения, сжатия
Понятие абсолютной и относительной деформаций
В каких сечениях стержня действуют наибольшие по величине нормальные и касательные напряжения
Закон Гука
Методы расчета на прочность (по допускаемым напряжениям, по разрушающим нагрузкам)
Условия прочности и жесткости
Виды расчетов (проектировочный, проверочный, эксплуатационный)
Определять деформацию растяжения, сжатия из совокупности других деформаций
Строить эпюры продольных сил, нормальных напряжений
Выполнять проектировочный, проверочный и эксплуатационный расчеты из условий прочности и жесткости
Выполнять проектировочный, проверочный расчеты про-  стейших статически неопределимых систем из условия прочности при различных внешних воздействиях
стейших статически неопределимых систем из условия прочности при различных внешних воздействиях
Понятие статически неопределимых стержневых систем. Их особенности. Способ раскрытия статической неопределимости 
Технику и методы механических испытаний материалов на растяжение, механические характеристики материалов
65

Введение Растяжение, сжатие
Два кирпича положили. Приступим к третьему.
Модуль В. Сдвиг. Кручение
Основные цели данного модуля:
1)научить определять деформацию чистого сдвига (кручение, срез) из совокупности других простых деформаций;
2)освоить методики проверочного, проектировочного и эксплуатационного расчетов круглых стержней из условий прочности и жесткости.
66

Схема 38. Взаимосвязь модуля «Сдвиг. Кручение» с другими дисциплинами и модулями
Теоретическая механика 
ИЗУЧИТЕ в разделе «Статика»
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
|
|
Теория пар сил. Условия равновесия |
|
|
||||||||||||
|
|
систем пар сил [82-83] |
|
|
||||||||||||
|
|
Приведение произвольной системы |
|
|
д |
|||||||||||
|
|
сил к заданному центру. Проекции |
|
|
||||||||||||
|
|
главного вектора и главного момента |
|
|
в |
|||||||||||
|
|
на оси координат [82-83] |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г. |
|
|
|
|
|
|
Математика |
||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ИЗУЧИТЕ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
График линейной функции; вычисление |
|
|
р |
||||||||||||
|
определенного интеграла, тригонометри- |
|
|
|||||||||||||
|
ческие функции; признаки подобия тре- |
|
|
у |
||||||||||||
|
угольников; решение систем линейных |
|
|
|||||||||||||
|
алгебраических уравнений [86-91] |
|
|
ч |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Сопротивление материалов |
|
н |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
Повторите |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Модуль Г
Модуль Д
Модуль Е
Модуль К
Модуль Л
Метод сечений (модуль А)
Модуль Г. Геометрические характеристики плоских сечений (если этот модуль изучен)
67
4.4.1. Входной контроль знаний
Математика
1.Нарисуйте график линейной функции.
2.Нарисуйте график синуса и косинуса угла.
3.Назовите признаки подобия треугольников.
4.Как вычислить длину дуги окружности?
5.Какая система координат называется полярной? Нарисуйте эту систему координат.
6.Чему равна площадь треугольника, круга, прямоугольника?
7.Как решается система алгебраических линейных уравнений?
8.Что называется производной функции?
9.Как вычислить определенный интеграл по поверхности?
Теоретическая механика
1.Чему равен момент силы относительно оси?
2.Чему равен момент силы относительно точки?
3.Запишите условия равновесия произвольной пространственной системы сил.
4.Запишите условия равновесия произвольной плоской системы сил.
5.Что называется парой сил? Как она изображается на расчетных схемах?
6.Чем определяется действие пары сил на тело?
7.Сформулируйте и запишите условия равновесия системы пар сил на плоскости.
8.Что называется главным моментом системы сил?
Сопротивление материалов
1.Ответьте на вопросы самоконтроля модулей А и Б и пройдите тестовый контроль по тестам модуля А [43] и программным вопросам [49].
Для восстановления знаний воспользуйтесь учебниками и справочника-
ми [82-91].
4.4.2. Изучение теории
Ознакомьтесь с информационно-логической схемой 39. Информационные блоки схемы показывают, какие понятия, системы понятий, расчетные методы и др. необходимо изучить в данном модуле.
|
Рекомендуем прочитать |
|
|
|
|
|
|
|
|
|
|
[52], Глава 5 |
|
[54], Глава 2 |
|
|
|
|
|
|
|
|
|
[59], Глава 3 |
|
[60], Глава 5 |
|
|
|
|
|
68

Схема 39. Чистый сдвиг, кручение
Внутренний силовой фактор – |
|
|
Внутренний силовой фактор – крутящий |
|
|
|||||||||||||||||
поперечная сила Q |
|
|
|
|
момент Т |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Деформация сдвига |
|
|
|
|
|
|
|
|
|
Деформация кручения |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Относительный угол |
|
|
Напряжения при чистом сдвиге и кручении |
|
|
|
||||||||||||||||
сдвига γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Касательные |
|
|
|
Главные |
|
|
|
|||||||
|
|
Закон Гука |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при чистом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сдвиге |
|
|
|
|
|
|
|
|
Угол закручивания, φ |
|
|
||||||||||
|
|
τ= Gγ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Относительный угол закручивания θ |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Испытание мате- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
риалов на круче- |
|
|
|
Условия прочности |
|
|
|
Условия жесткости |
|
|
||||||||||||
ние |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
При сдвиге (срезе): |
|
При кручении: |
|
|
При кручении: |
|
|
|||||||||||||||
|
|
Q |
|
|
|
|
T |
|
|
|
|
T |
|
|
||||||||
|
|
τmax = A ≤ τadm |
|
|
τmax =Wp ≤ τadm |
|
|
|
θmax = |
|
≤ θadm |
|
|
|||||||||
|
|
|
|
|
|
|
GJp |
|
|
|||||||||||||
Расчеты на прочность и жесткость при сдвиге и кручении
Методические указания к изучению модуля Изложение теории начинается с введением дополнительных гипотез к
тем, что приняты при моделировании свойств материала детали. Обратите внимание, в чем суть дополнительных гипотез и попытайтесь оценить последствия непринятия этих гипотез.
Научитесь выделять из сложного нагружения (сложного сопротивления)
69
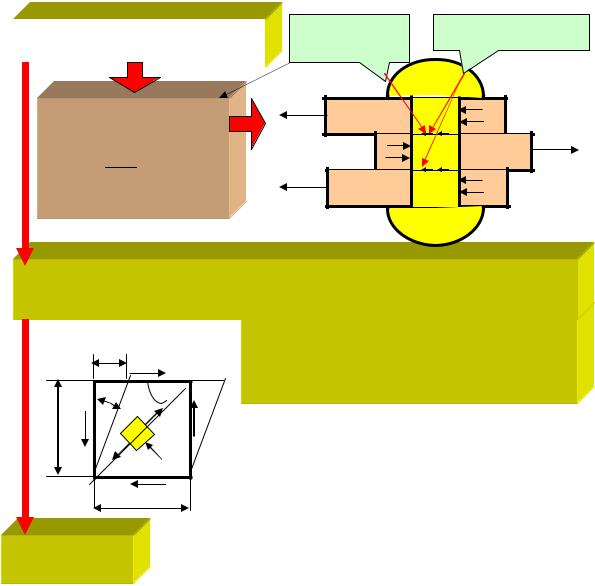
|
|
Деформация сдвига |
Касательные |
Плоскости среза |
|
|
напряжения |
|
|
|
|
|
|
|
|
|
|
|
|
Сдвиг (срез)
τ= 2AF ≤ τadm
F |
F |
|
Чистый сдвиг
σmax =σ1 =−σ2 =τ
|
Нормальные напряжения максимальны на |
∆а |
площадках, наклоненных к площадкам чис- |
τтого сдвига на угол 45o
γσ 45
аτ  2 σ1 τo
2 σ1 τo
σ1 |
σ2 |
∆a |
= tgγ ≈ γ - относительныйугол сдвига |
|
a |
|
|
а |
τ |
(угол γ в радианах) |
|
|
|
||
Деформация
кручения
Схема 40. Срез, чистый сдвиг
деформацию кручения. Обратите внимание на то, что в в сечении, где приложен сосредоточенный момент, мы имеем два значения крутящего момента: один принадлежит сечению предыдущего участка, другой – последующего. Попытайтесь объяснить причину этого явления.
Постарайтесь запомнить условия прочности при срезе и кручениии, а также условие жесткости при кручении. Обратите внимание на то, как распределены касательные напряжения по плоскостям поперечных и продольных сечений круглого вала. Полученные формулы при изучении деформации кручения могут быть применены только к круглым валам.
Обратите внимание на то, что в статически неопределимых задачах крутящий момент в ступенчатом валу распределяется в зависимости от жесткости участков вала GЈp/li.
70
