Чтобы учесть эту и подобные ей ситуации, естественно ввести следующее распределение: максимальный k-связный подграф графа называется егоk-связной компонентой, или простоk-компонентой.

Это определение иллюстрируется на рис. 33.4. На рисунке граф G1 имеет две 2-компоненты, а G₂ —

две 3-компоненты. Сами графы G1 и g2 являются 1-компонентами графа G1 U G2. Легко заметить, что 2-компоненты графа G1 имеют одну общую вершину, а 3-компоненты графа gz — две общие вершины. Следующая теорема показывает, что это обстоятельство не случайно.

Теорема 33.4. Две различные k-компоненты графа имеют не более чем k-- 1 общих вершин.

Пусть G1 и G2 — различные K-компоненты графа G и VG1VG₂ = X. Предположим, что |Х|k, и докажем, что тогда граф G1 U G2 должен быть k-связным. Для этого в данном случае достаточно показать, что он остается связным после удаления любых k — 1 вершин, т. е. если Y U V(G1UG₂), |Y| =k-1, то граф (G1 U G2)-Y связен. Положим

связны. Так как по предположению |Х| k, то Х\Y₃не равно =, т. е. связные графы H₁ и H₂ имеют хотя бы одну общую вершину. Следовательно, связен граф H₁U H₂ = =(G₁ U G₂)— Y. Последнее означает, что граф G\ U G₂ k-связен. Поэтому, вопреки предположению, ни G₁, ни G₂ не являются k-компонентами графа G.

§ 34. Двусвязные графы

Случаям, когда k = 2 или k = 3, в теории графов отведена особая роль. Это объясняется следующими причинами. Во-первых, 2- и 3-связные графы фигурируют во многих теоретических и прикладных вопросах, в частности, ряд задач достаточно уметь решать для 2-связных компонент. Во-вторых, при k = 3 и, особенно, при k = 2 удается дать в некоторой степени обозримое описание соответствующих графов.

Рассмотрим вначале некоторые простые свойства 2-связных графов, вытекающие непосредственно из определений:

1. степени вершин 2-связного графа больше единицы

2. если графы G₁ и G₂ 2-связны и имеют не менее двух общих вершин, то граф G₁ U G₂ также 2-связен;

3. если граф G 2-связен и Р — простая цепь, соединяющая две его вершины, то граф G U Р также 2-связен;

4. если вершина v не является точкой сочленения cвязного графа, то любые две его вершины соединены цепью, не содержащей v, в частности, в 2-связном графе для любых трех несовпадающих вершин а, b, v имеется (a, b)-цепь, не проходящая через v.

Этими свойствами мы будем пользоваться без каких-либо пояснений и дополнительных ссылок на них.

Теорема 34.1. Пусть G—связный граф и |G| > 2. Тогда следующие утверждения эквивалентны'.

1. граф 2-связен;

2. любые две вершины графа принадлежат простому циклу;

3. любая вершина и любое ребро принадлежат простому циклу;

4. любые два ребра принадлежат простому циклу;

5. для любых двух вершин а и b и любого ребра е существует простая (а, b}-цепъ, содержащая е;

6. для любых трех вершин а, b, с существует простая (а, b)-цепь, проходящая через с.

t> 1) =>2). Пусть а и b — две вершины графа G. Расcмотрим множество всех простых циклов графа G, содержащих а. Обозначим через U множество всех вершин, входящих в эти циклы. Ясно, что U не= пустое множество. Действительно, простой цикл, содержащий а, можно получить, объединив два ребра ах и ау (х не=у) и простую (х, у)-цепь,

не проходящую через а (существующую согласно свойству 4)). Предположим, что b не принадлежит U, и положим неU = VG\U. Поскольку граф G связен, то в нем найдется такое ребро zt , что z принадлежитU, t U (рис. 34.1). Пусть S— простой цикл, содержащий а и z. Так как G — 2-связный граф, то в нем имеется простая (a,t)-цепь Р, не содержащая z. Пусть v — первая, считая от if, вершина, входящая в S, т.е. (t, v)-подцепь цепи Р не имеет с S общих вершин, отличных от v. Теперь легко построить простой цикл, содержащий а и t. Он получается объединением (v, z)-цепи, входящей через а и являющейся частью S, с ребром и (t, v)-подцепью цепи Р (на рис. 34.1 этот цикл показан пунктирной линией). Следовательно, tU; но это противоречит выбору ребра zt. Таким образом, неU =, т.е. а и b лежат на общем простом цикле 2)=>3). Пусть а —вершина и zt — ребро графа G условию G содержит цикл S, проходящий через вершины верны а и z. Не теряя общности будем считать, что zt . S. Если при этом окажется, что S проходит через вершину t, то требуемый цикл строится очевидным образом. Пусть S не проходит через t. Тогда рассмотрим простой цикл S', проходящий через вершины t и а. Такой цикл, по условию, существует. Частью этого цикла является простая цепь Р, соединяющая t с некоторой вершиной v . S. Цепь Р можно выбрать так, чтобы VP 

VS={v}. Искомый цикл теперь строится точно так же, как в предыдущем пункте.

3)=> 4). Пусть аb и tz — два ребра графа G. По условию G имеет простые циклы S и S', первый из которых содержит аb и z, а второй — аb и t. Далее искомый цикл строится так же, как в предыдущих пунктах.

4) =>5). Пусть a, .VG, tz.EG. Будучи связным, граф G содержит простую цепь Р = (а, х, ..., b). Согласно утверждению 4) в графе G есть простой цикл S, содержащий ребра ах и tz. Легко видеть, что в объединении S U P имеется требуемая цепь.

5)=>6). Пусть а, b, cVG, cd.EG. По условию в графе имеется простая (а, b)-цепь, проходящая через cd и, следовательно, содержащая с.

6)=> 1). Пусть v . VG. Покажем, что граф G — v связен, т. е. любая пара а, b его вершин соединена цепью. Действительно, согласно утверждению 6) в графе G имеется простая (v, b)-цепь, проходящая через вершину а. Эта цепь содержит (а,b)-подцепь, которая, очевидно, не проходит через v и, следовательно, является (а,b}~ цепью и в графе G — v.

Если в формулировке теоремы 34.1 заменить всюду слова «простая цепь» и «простой цикл» соответственно на слова «цепь» и «цикл», то получим аналогичную теорему о 2-реберно-связных графах.

Как отмечалось выше, при решении многих задач на графах достаточно уметь решать эти «задачи для каждой 2-связной компоненты графа. Поэтому представляет интерес взаимное расположение 2-компонент в графе.

М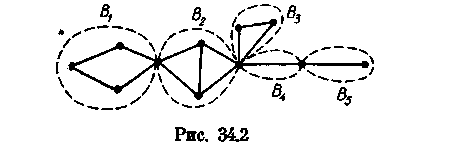аксимальные относительно включения элементымножества связных подграфов графа G, не имеющих точек сочленения, называются его блоками. Таким образом, каждый блок графа либо 2-связен, либо совпадает с К₂ или с К₁ (граф К₁ — блок тогда и только тогда, когда он является связной компонентой). Связный граф без точек сочленения также называют блоком. Множество вершин блока будем называть блоковым множеством.

Например, граф, изображенный на рис. 34.2, содержит пять блоков B_i (i = 1, 5) (они обведены пунктирными линиями). Среди этих блоков В₁, В₂ и В₃ — 2-связ-ные графы, а каждый из двух оставшихся является ребром.

Утверждение 34.2. Любые два блока графа имеет не более одной общей вершины. В частности, всякое ребро графа входит только в один его блок.

Утверждение 34.3. Если блок графа содержит вершины а и b, то он содержит и всякую простую а, b)-цепь этого графа.

Утверждение 34.4. Если вершина v входит более чем в один блок графа G, то v — точка сочленения этого графа.

Эти утверждения непосредственно следуют из перечисленных в начале параграфа простейших свойств 2-связных графов и теоремы 34.1.

Следствие 34.5. Система блоковых множеств графа является покрытием множества его вершин. Каждая пара блоковых множеств либо не пересекается, либо имеет единственную общую вершину, и эта вершина является точкой сочленения графа.

Следующая конструкция дает представление о структуре графа «с точностью до блоков». Пусть В ={Bi} и = (с_j} — соответственно множества блоков и точек сочленения графа G. Сопоставим с G граф bc(G), у которого В U С — множество вершин и (B_iс_j :B_i . В, с_j  С, c_j .B_i — множество ребер. Тем самым, ребра двудольного графа bc(G) указывают на принадлежность точек сочленения блокам. На рис. 34.3 представлены графы G и bc(G).

Утверждение 34.6. Если граф G связен, то bc(G)— дерево.

Очевидно, что из связности графа G вытекает связность графа bc(G). Предположим, что bс (G) содержит

цикл С. Пусть этот цикл имеет вид С= (с_j,b_j с_j2, b_j2, .. ., c_jl b_jl, c_j1). Каждый из блоков B_ik содержит (C_jk, c_jk+1)-цепь и объединение этих цепей дает простой цикл в графе G. Обозначим этот цикл через С'. Ясно, что С' содержит по крайней мере две вершины каждого из блоков Bi_k. Поэтому из утверждения 34.3 следует, что цикл С' должен содержаться в каждом из этих блоков. Последнее означает, что каждая пара блоков B_ik имеет.не менее |С'|  3 общих вершин. Получаем противоречие с утверждением 34.2. <

Граф bc(G) называется bc-деревом связного графа G. Блоки графа G, соответствующие концевым вершинам его bс-дерева, называются концевыми блоками.

Похожее представление графа можно получить, положив в основу его максимальные реберно-2-связные подграфы, т. е. максимальные связные подграфы, не содержащие мостов. Такие подграфы называют листами. Не останавливаясь на деталях, заметим следующее. Каждая вершина графа порядка n > 1 принадлежит в точности одному листу и каждое ребро, не являющееся мостом, входит только в один лист. Таким образом, граф состоит из листов и мостов, соединяющих некоторые из них. Для описания строения графа «с точностью до листов» можно ввести граф, аналогичный графу bc (G). Вершины такого графа биективно соответствуют листам графа G и две его вершины соединены ребром в том и только в том случае, когда соответствующая пара листов G соединена мостом. Можно показать, что введенный таким образом граф является деревом, если исходный граф связен.

На рис. 34.4 граф G имеет 5 листов L₁, L₂, L₃, l₄, L₅ и 4 моста, а граф G' показывает, как связаны между собой листы графа G.

Приведем некоторые результаты о трехсвязных графаx, которые будут использованы в главе «Планарность».

Пусть G — связный граф, Н — некоторый его подграф. Простую открытую цепь v₁, v₂, ..., v_k, k) 3, графа назовем Н-цепью, если выполняются условия

v₁  VH, v_k . VH, v_t . VH, i = 2, k - 1.

Ребро е = uv графа G также будем называть Н-цепью, если и . VH, v . VH, е . ЕН.

Лемма 34.7. Пусть G — двусвязный граф. Тогда для всякого его подграфа Я, содержащего более одной вершины отличного от G , существует Н-цепь графа G.

Если G — остовный подграф, то любое ребро графа не входящее в ЕН, служит H-цепью.

Пусть подграф G не является остовным. Рассмотрим три попарно различные вершины и  VH, v . VH, w . VН. По теореме 34.1 в графе G есть простая (и, v)-цепь, проходящая через w. Очевидно существование подцепи этой цепи, являющейся Н-цепью графа G. Ниже для и, v . VG положим G_uv = G — и — v. Теорема 34.8. Во всяком 3-связном графе G есть такое ребро uv, что граф G_uv не имеет точек сочленения.

Если |G| = n = 4, то утверждение теоремы очевидно. Поэтому будем считать, что n  5. имеет хотя бы одну точку сочленения. Тогда из 3-связ-еости графа G следует, что при любом выборе ребра uv . EG граф G_uv обладает следующими свойствами (рис. 34.5):

1. если а — висячая вершина графа G_uv, то av.EG, аи . EG;

2. всякий висячий блок графа G_uv, не являющийся ребром, содержит такую пару вершин с и d, отличных от точек сочленения графа G_uv, что

uc.EG, vd .EG;

3. всякий блок графа G_uv, имеющий ровно две точки сочленения и отличный от ребра, содержит такую вершину l, неявляющуюся точкой сочленения графа G_uv, что u_lEG или v_l . EG.

Обозначим черезB_uv максимальный по числу вершин блок графа G_uv, а через t_uv — число вершин в этом блоке. Теперь выберем ребро uv так, чтобы число t_uv было наибольшим

Предположим противное, т. е. что для любого ребра uv.EG граф G_uv

Покажем, что в этом случае t_uv  3. Пусть t_uv = 2 и а — висячая вершина графа G_uv (являющегося деревом). Так как п)5, то существует ребро cd EG_uv, , с ≠ а, d≠a. Из свойства 1) вытекает, что в графе G_cd существует цикл (и, a, v, и), т. е. t_cd > t_uv. Получено противоречие, следовательно, t_uv 3.

Через D_uv обозначим bс-дерево графа G_uv и рассмотрим следующие случаи.

1. Дерево D_uv не является цепью. Выберем в этом дереве цепь, соединяющую пару висячих вершин и проходящую через вершину, соответствующую блоку B_uv. Этой цепи соответствует последовательность В1, ..., В_р блоков графа G_uv, среди которых содержится блок B_uv, причем блоки В₁ и В_р являются висячими (рис. 34.6).

Пусть В' — произвольный висячий блок графа G_uv, отличный от В₁ и В _р. Из свойств 1) и 2) вытекает существование таких отличных от точек сочленения графа G_uv вершин а . VB1, b . VB_P, с . VB', что ис EG,

va . EG, vb EG. Тогда в графе G_uс вершины множества р U VBi U v входят в один блок и, следовательно, t_uv <t_uc. Последнее противоречит выбору ребра uv.

2. ДеревоD_uv — цепь и B_uv — блок графа G_uv, не являющийся висячим. Пусть b1, ..., Вр — последовательность всех блоков графа G, причем блоки В1 и В_р — висячие, B_i П B_i+1 не= пустое0 (i = 1,р-1), B_uv = B_k (1<k<p) рис. 34.7). Согласно свойству 3) найдется вершина b . VB_uv, отличная от точек сочленения графа G_uv, смежная с и или с v. Пусть иb . EG. Согласно свойствам 1) 2) существуют

такие отличные от точек сочленения графа G_uv вершины а . VB₁, c .VB_P, что uс .EG, vc . EG. Легко видеть, что в графе G_vc имеется блок, содержащий все вершины множества U VB_i U u. Поэтому

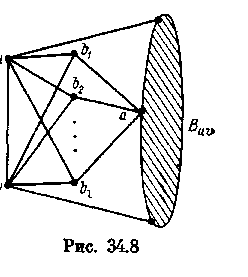
t_vc> t_uv, и снова получаем противоречие. 3. Дерево D_uv — цепь и B_uv — висячий блок графа C_uv. Если граф G_uv содержит такое ребро ху, что VB_uv П {х, у}=пустое множество, то, используя свойство 2), легко показать, что в графе G_xy есть блок, содержащий множество верен VB_uv U {и, v}, а, значит t_uv < t_xy. Так как B_uv — висячий блок графа G_uv, то последнее означает, что граф G_uv cocтоит из блока B_uv и ребер ab1,ab2 ..., ab_t (рис. 34.8). 3-связности графа G следует, что граф G — а не имеет точек сочленения. Поскольку в графе G — а вершина b₁ смежна только с вершинами и и v, a uv . ЕG, то граф B_ab1 также не имеет точек сочленения, что противоречит предположению.

Таким образом, показано, что во всяком 3-связном графе G существует такое ребро uv, что граф G_uv, не имеет точек сочленения.

Следствие 34.9. Всякий 3-связный граф с числом вершин n )5 содержит ребро, стягивание которого приводит к 3-связному графу.

Доказательство также проведем от противного. Пусть, стягивая некоторое ребро x=uv 3-связного графа G в вершину х, получаем граф G_x, для которого

K(G_x) = 2. (Равенство K(G_x)=1 невозможно в силу 3-связности графа G.) Тогда в графе G_x существуют две вершины, удаление которых делает его несвязным. Одной из них должна быть х (в противном случае K(G)=2). Удалению вершины х из G_x соответствует удаление вершин и и v из графа G. Поэтому для любого ребра х =uv . EG граф G имеет такую вершину w, что граф G — u — v — w несвязен. Вершина w является точкой сочленения графа G_uv, что противоречит предыдущей теореме.

Отметим еще без доказательства следующую теорему (см. обзор [21]).

Теорема 34.10. Почти все графы двусвязны.

Поскольку каждый мост инцидентен точкам сочленения графа, то из этой теоремы вытекает

Следствие 34.11. Почти все графы не содержат мостов.