§ 2.2. Определение и простейшие свойства определителей

Определителем - го порядка, соответствующим квадратной матрице порядка , называется алгебраическая сумма членов, составленная следующим образом: членами суммы служат всевозможные произведения элементов матрицы, взятых по одному в каждой строке и в каждом столбце, причем член берется со знаком плюс, если перестановка содержит четное число инверсий, и со знаком минус- в противном случае. При этом инверсией чисел и называется ситуация, в которой , но стоит в перестановке раньше, чем . Для определителя матрицы будем использовать обозначения или .

Определители первого, второго и третьего порядков вычисляются по формулам, вытекающим непосредственно из определения:

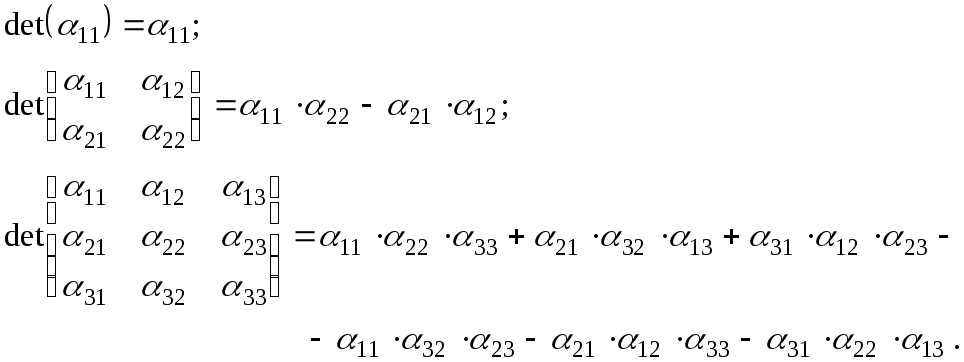
При вычислении определителей третьего порядка удобно пользоваться “правилом треугольников”, отраженным по следующей схеме:

+ ¾

Из определения определителя следует, что:

.

Таким образом определитель диагональной, верхней и нижней треугольных матриц равен произведению диагональных элементов.

Основные свойства определителей:

Определитель не меняется при транспонировании.

. От перестановки двух строк (столбцов) определитель меняет знак.

. Определитель, содержащий две равные строки (столбца), равен нулю.

. Если все - строки (- го столбца) определителя представлены в виде суммы двух слагаемых, то и весь определитель представляется в виде суммы двух определителей, у которых все строки (столбцы), за исключением - й (- го), такие же, как в исходном определителе, а - я строка (- й столбец) в первом определителе состоит из первых слагаемых и во втором- из вторых. Например:

. Если все элементы некоторой строки (столбца) умножить на число, то определитель умножится на это число. Общий множитель элементов строки (столбца) определителя можно выносить за знак определителя. Если все элементы определителя умножить на число , то определитель умножится на .

. Если одна из строк (один из столбцов) определителя состоит из нулей, то определитель равен нулю.

. Определитель не меняется, если к элементам одной его строки (столбца) прибавить соответствующие элементы другой его строки (столбца), умноженные на одно и то же число.

Пример 1. Определите число инверсий в перестановке 2,3,8,1,4,5,7,6.

Решение. Поскольку 2 стоит в перестановке раньше, чем 1, 2 образует в перестановке одну инверсию. 3 также образует одну инверсию, 8- пять инверсий, т.к. стоит раньше, чем 1,4,5,7 и 6. Продолжая, получаем, что общее число инверсий в перестановке

Пример 2. Пользуясь только определением, вычислите определитель.

Решение. В соответствии с формальным определением определителя

Запишем все ненулевые произведения элементов матрицы и соответствующие им перестановки:

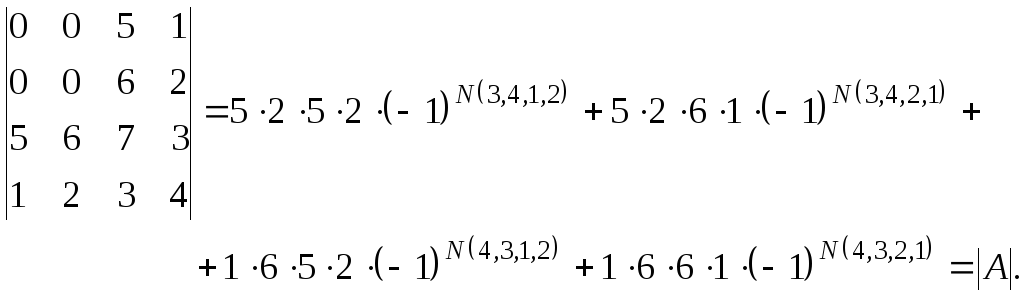
Учитывая, что

окончательно получаем:

Пример 3. Применяя свойства, вычислите определитель .

Решение. Для вычисления определителя воспользуемся методом приведения его к верхнему треугольному виду. Метод заключается в преобразовании определителя к такому виду, где все элементы, расположенные ниже главной диагонали, равны нулю. Полученный определитель равен произведению элементов главной диагонали.

Переставим первую и четвертую строки определителя. Определитель изменит знак:

Первую строку последнего определителя, умноженную на , прибавим ко второй его строке; первую строку, умноженную на , прибавим к третьей строке; первую строку, умноженную на , прибавим к четвертой строке. Получим:

.

Переставим вторую и третью строки полученного определителя; вынесем общий множитель элементов второй строки за знак определителя. Получим:

.

Вторую строку определителя, умноженную на , прибавим к третьей строке; вторую строку, умноженную на , прибавим к четвертой строке. Имеем:

.

Переставим третью и четвертую строки. Третью строку полученного определителя, умноженную на , прибавим к четвертой строке. Приходим к определителю верхней треугольной матрицы

,

который вычисляется просто:

.

2.2.1. Входят ли в определитель - го порядка произведения:

2.2.2. С каким знаком в определитель - го порядка входят произведения:

2.2.3. Подберите и так, чтобы произведение входило в определитель - го порядка со знаком плюс.

2.2.4. Запишите (пользуясь определением) определитель четвертого порядка в развернутой форме.

2.2.5. Пользуясь только определением, вычислите определители:

2.2.6. Вычислите определители:

где где

2.2.7. Применяя свойства, вычислите определители:

2.2.8. Не развертывая определителей, докажите следующие тождества: