Глава 2 Матрицы и определители

§ 2.1. Действия с матрицами

Прямоугольной или - матрицей называется совокупность чисел из поля , расположенных в виде таблицы

Кратко матрицу записывают в виде Числа , составляющие данную матрицу, называют ее элементами. Первый индекс у элемента указывает номер строки, а второй- номер столбца, на пересечении которых находится этот элемент.

Матрицу называют комплексной, если хотя бы один ее элемент является комплексным числом, и действительной, если все ее элементы- действительные числа.

Две матрицы одинакового размера считают равными, если попарно равны их соответствующие элементы, т.е. элементы, стоящие на одинаковых местах в этих матрицах.

Матрицу, состоящую из одной строки или одного столбца, называют соответственно вектор- строкой или вектор- столбцом. Элементы векторов называют их компонентами. Матрица, состоящая из одного числа, отождествляется с этим числом.

Матрица, состоящая из нулей, называется нулевой и обозначается .

Если число строк матрицы равно числу ее столбцов, то матрицу называют квадратной порядка . Диагональ квадратной матрицы, соединяющая левый верхний угол с правым нижним, называется главной. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называют диагональными. Примером диагональных матриц является единичная матрица

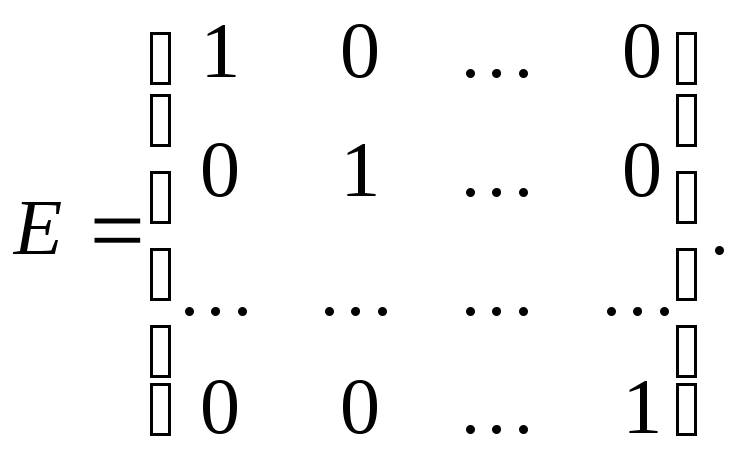
Матрицу, полученную из данной матрицы заменой в ней строк соответствующими столбцами, называют транспонированной к и обозначают через . Если - - матрица, то - - матрица. В частности, если - вектор- строка, то - вектор- столбец и наоборот.

Суммой матриц одинакового размера называется матрица того же размера, элементы которой равны суммам соответствующих элементов слагаемых матриц. Таким образом

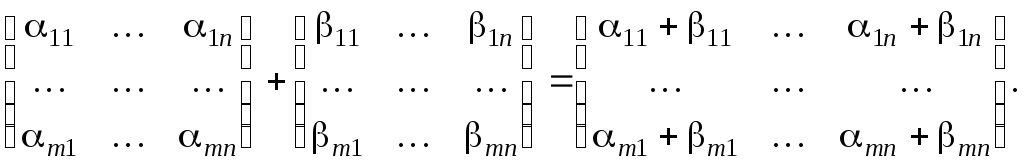
Разность матриц определяется аналогично:

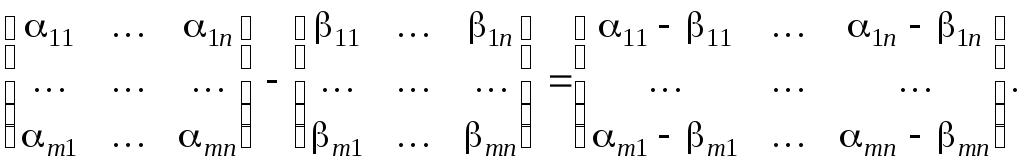
Произведением матрицы на число называют матрицу , все элементы которой равны произведениям соответствующих элементов исходной матрицы на это число:

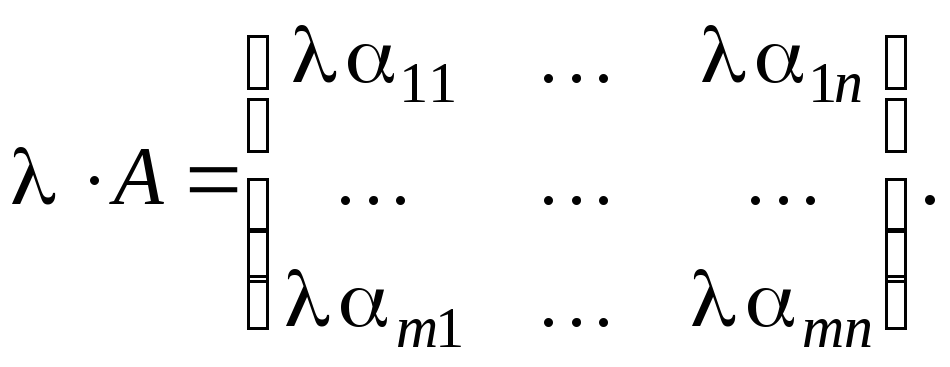
Сложение матриц и умножение их на числа обладают следующими свойствами:

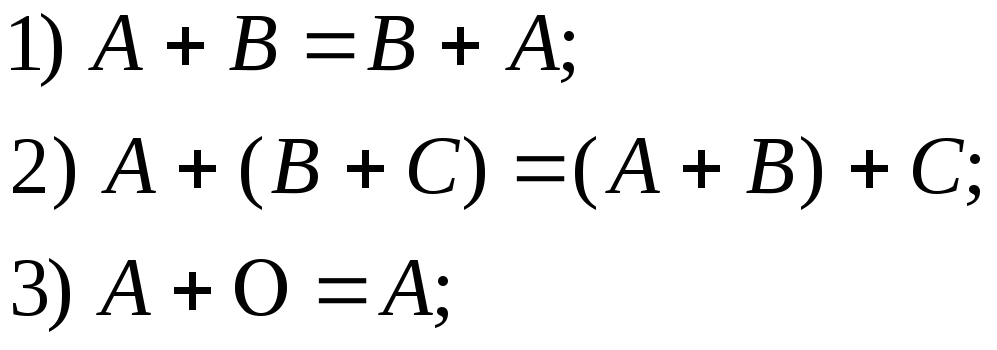
где

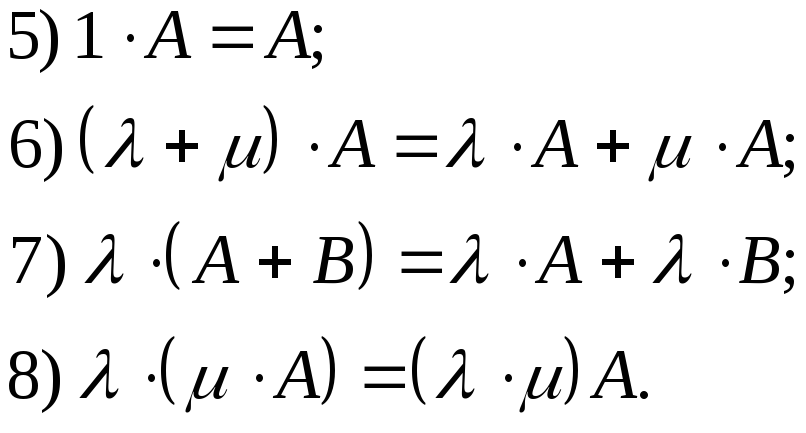
при любых матрицах и любых числах

Умножение матриц определяется лишь для случая, когда число столбцов первого множителя равно числу строк второго множителя. Пусть

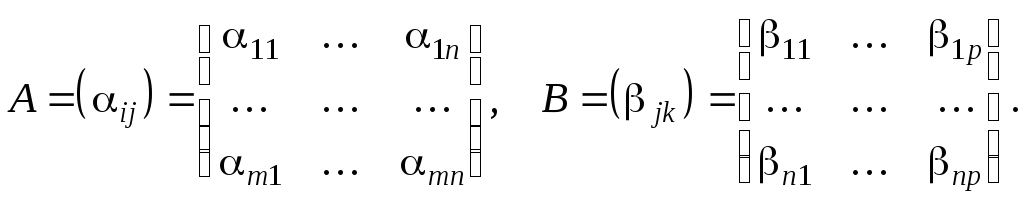
Произведением матриц и , заданных в указанном порядке, называется матрица , элементы которой определяются по следующему правилу:

т.е. элемент матрицы равен сумме произведений элементов - строки матрицы на соответствующие элементы - го столбца матрицы . Из этого определения следует, что матрица будет матрицей размера .

Умножение матриц обладает следующими свойствами:

в общем случае (если для каких-либо матриц и выполняется равенство , матрицы называются перестановочными);

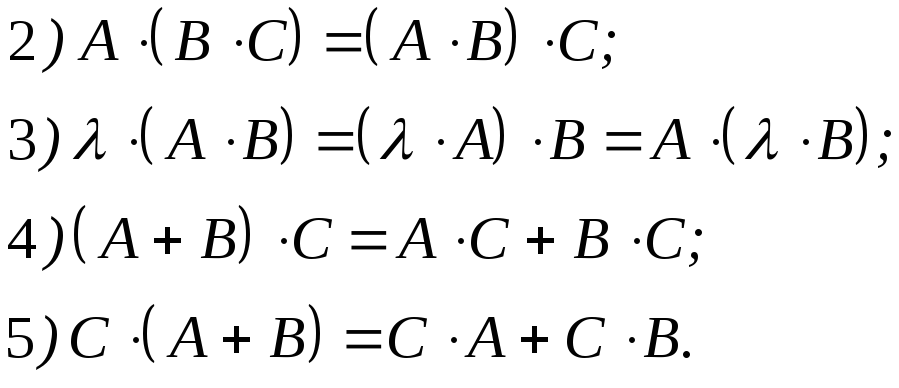
Отметим некоторые свойства операции транспонирования матриц:

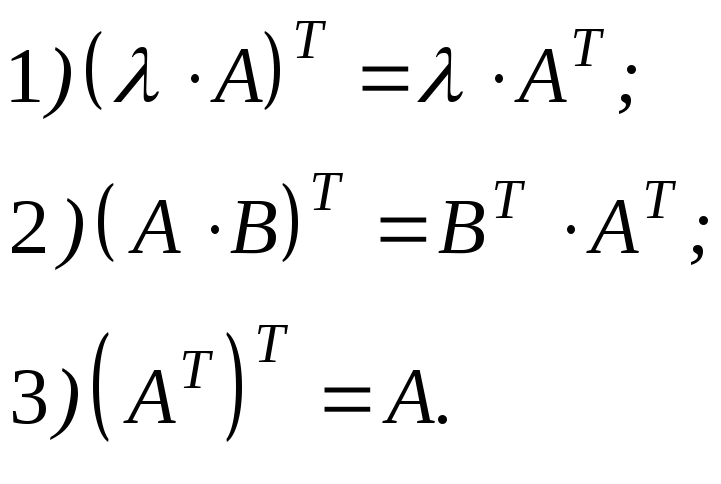
Пример 1. Найдите матрицу , удовлетворяющую равенству , где

Решение. Исходя из свойств линейных операций над матрицами, равенство равносильно равенству Таким образом,

Пример 2. Вычислите и при

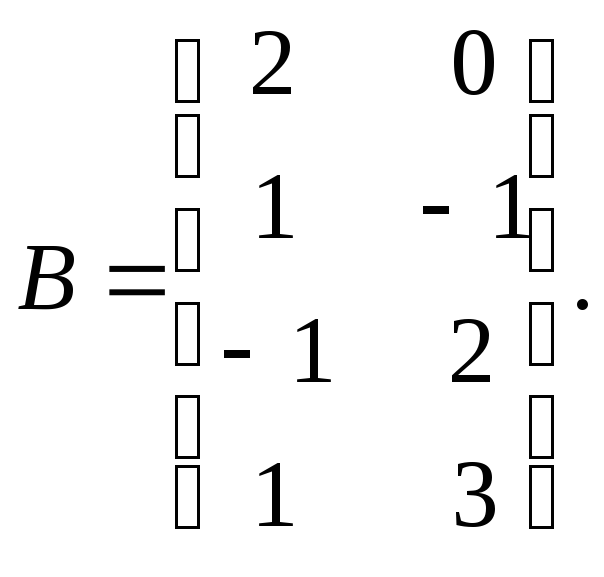
Решение. Произведение имеет смысл, так как число столбцов матрицы равно числу строк матрицы . Поэтому

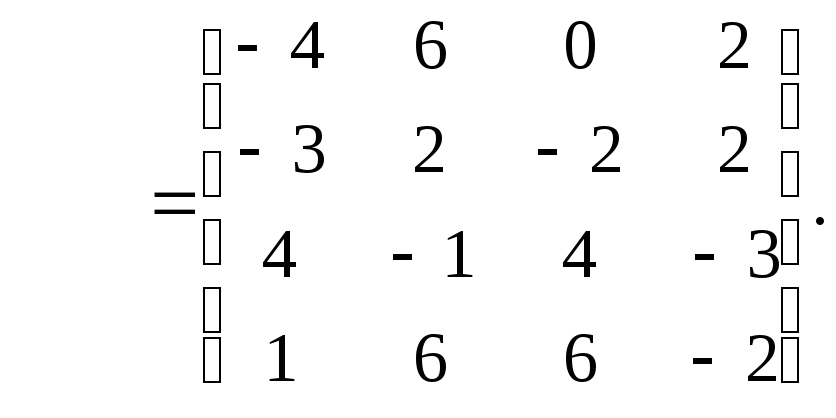
Произведение также имеет смысл, поскольку число столбцов матрицы равно числу строк матрицы .

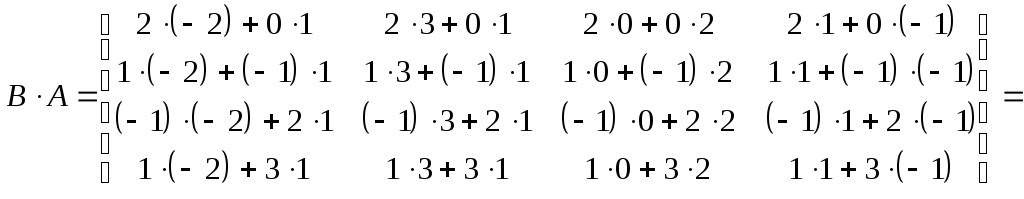
Пример 3. Найдите , если

Решение. Подставляя в многочлен вместо матрицу и учитывая, что , получаем

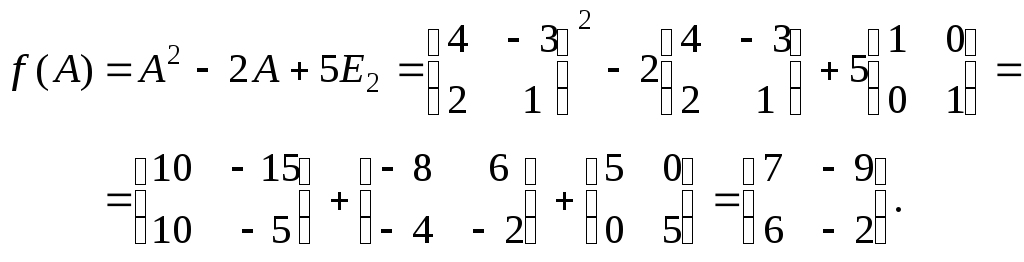
2.1.1. Найдите матрицу , удовлетворяющую условию:

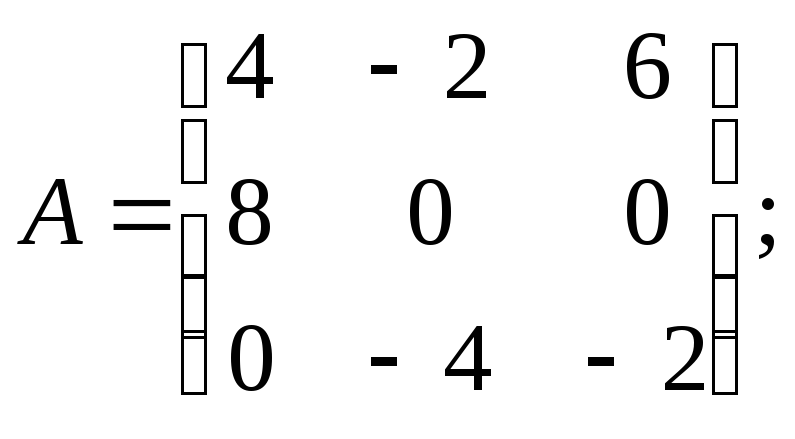
где

где

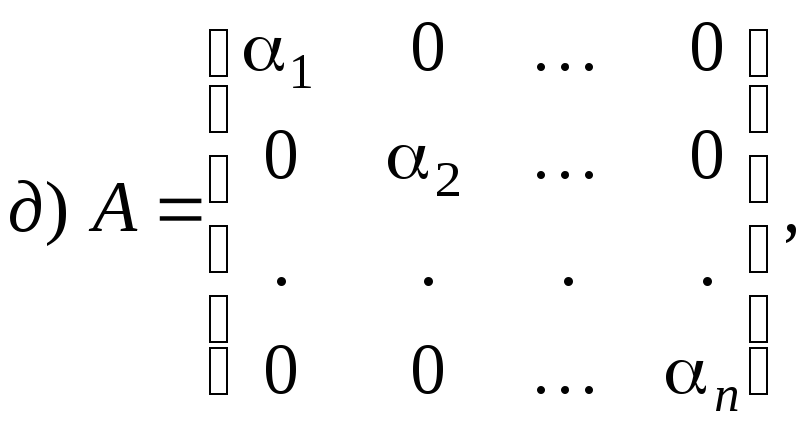
2.1.2. Найдите сумму матриц , разность матриц и произведения матриц и , если они существуют:

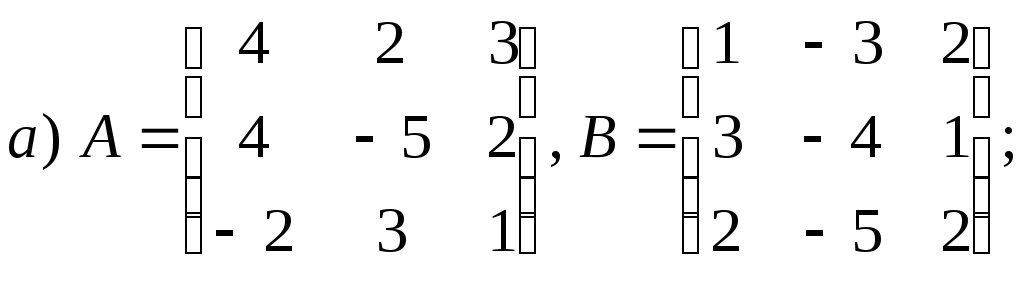
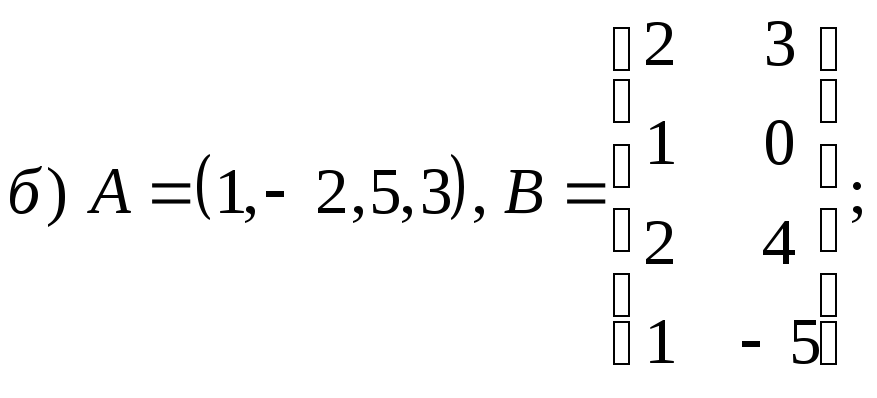
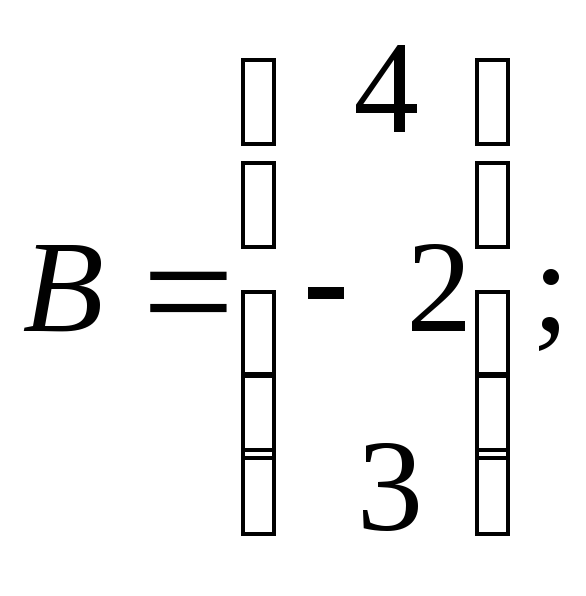
2.1.3. Вычислите если

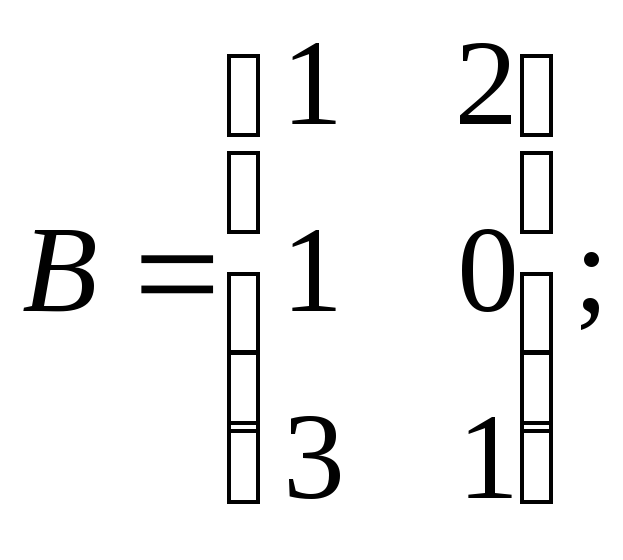
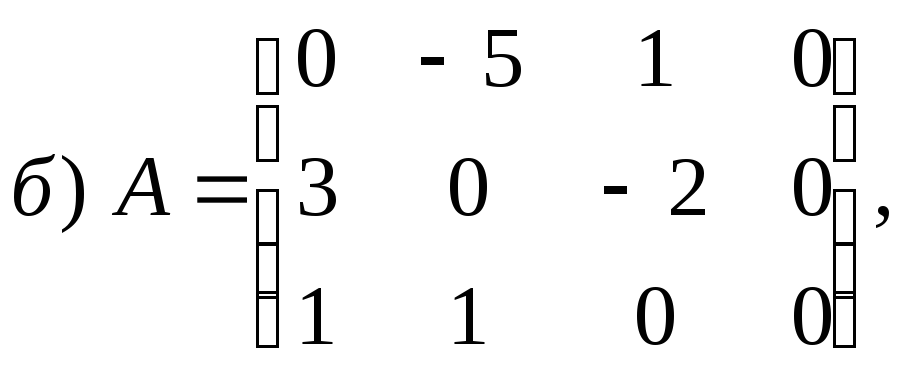
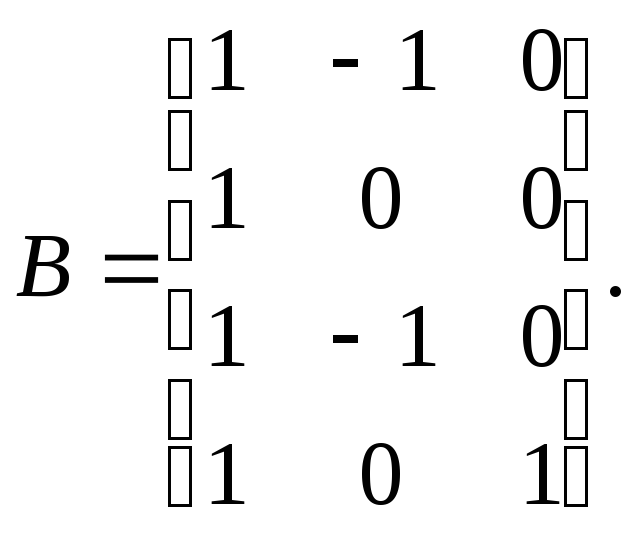
2.1.4. Вычислите:

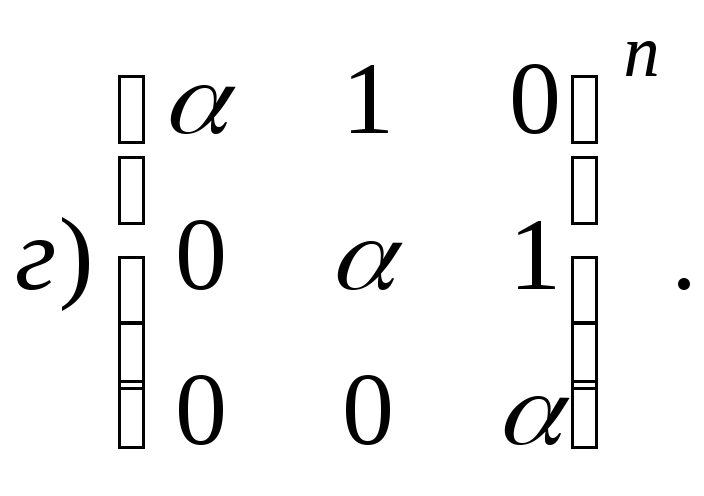
2.1.5. Найдите если

2.1.6. Докажите, что для перестановочных матриц и имеют место равенства:

Верны ли эти равенства, если ?