3Линейка / Экзамен / I семестр теория

Множество решений однородной системы линейных уравнений

(1)

Образует линейное пространство размерности , где - ранг матрицы системы. Любой базис пространства решений однородной системы называется фундаментальной системы решений этой

системы.

Если , то множество решений системы образует подпространство Fn, размерности (n-r) и базисом этого подпр-ва является ФСР.

36) Докажите, что сумма частного решения неоднородной СЛАУ и общего решения соответствующей однородной системы дает общее решение неоднородной системы.

Теорема: Общее решение Неоднородной СЛАУ является суммой общего решения соответствующей ОСЛАУ и частного решения неоднородной СЛАУ

►Доказательство: Рассмотрим систему уравнений

(1)

И соотвецтвующую ей однородную систему уравнений

Будет решением системы (2): если

И

То

Наоборот, если 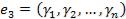–произвольное решение однородной системы (2), то строка

Будет удовлетворять системе (1): если

И

То

Отсюда следует, что все решения системы (1) можно получить, прибавляя к одному какому-нибудь ее решению всевозможные решения однородной системы (2). Иными словами goto условие Теоремы!◄

37) Определение евклидова пространства. Примеры евклидовых пространств.

Говорят, что в действительном линейном пространстве L определено скалярное произведение, если каждой паре векторов поставлено в соответствие действительное число обозначаемое (x,y) причем это соответствие удовлетворяет следующим аксиомам:

1)

2)

3)

4)

Действительное линейное пространство в котором определено скалярное призведение называется евклидовом.

Примером евклидого пространства может быть

(док-во справедливости аксиом скал произв в вопросе 40)

38) Неравенство Коши-Буняковского для евклидова пространства.

Для любых двух векторов x и y евклидова пространства справедливо неравенство Коши-Буняковского

►(λx-y,λx-y)=(λx,λx-y)-(y,λx-y)=(λx,λx)-(λx,y)-(y,λx)+(y,y)=λ2(x,x)- 2λ(x,y)+(y,y)

Этот квадратный трехчлен принимает не отрицательные значения его дискриминант D=b2-4ac=4(x,y)2-4(x,x)(y,y)

◄

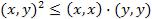Знак равенства имеет место тогда и только тогда, когда векторы x и y коллинеарные.

39) Докажите, что неравенство Коши-Буняковского обращается в равенство тогда и только тогда, когда векторы x и y коллинеарные.

►Достаточность

Пусть x и y коллинеарны и

=

Необходимость

Пусть теперь для некоторых x и y выполняется равенство

, если , векторы коллинеарны, если

можно выбрать

◄

40) Докажите, что в любом конечномерном действительном линейном пространстве можно ввести скалярное произведение.

Аксиомы выполняются

Введем ск.пр. как x1*y1+x2*y2+…+xn*yn для произвольных векторов x={x1,x2,…,xn} и y={y1,y2,…,yn}

Аксиома1: (x,y)=x1*y1+x2*y2+…+xn*yn=y1*x1+…+yn*xn=(y,x)

A2: (j*x,y)=(j*x1)*y1+…+(j*xn)*yn=j*(x1*y1+…+xn*yn)=j*(x,y)

A3:

(x+y,z)=(x1+y1)*z1+…+(xn+yn)*zn=(x1*z1+…+xn*zn)+(y1*z1+…+yn*zn

)=(x,z)+(y,z)

A4: (x,x)=x1*x1+…+xn*xn>=0 , (x,x)=0 только при xi=0, i=1..n, то есть при x={0,0,..,0}

Так как при вводе никаких ограничений на размерность кроме его конечности при вводе ск.пр. в действительном линейном пространтве не вводилось, то таким образом ск.пр. можно ввести в любом конечномерном деств. лин. пр-ве.

41) Нормированное пространство. Докажите, что всякое евклидово пространство является нормированным, если || x|| = √(x,x)

Вещественное или комплексное линейное пространство L называется нормированным пространством, если каждому вектору х из L поставлено в соответствии вещественное число ||x||, называемое нормой (длинной) вектора х, причем выполнены следующие аксиомы нормы:

1°) ||x||>0,если х≠Θ, ||Θ||=0;

2°) ||λx||=|λ|·||x|| для каждого х из L и каждого λ из R или C;

3°) ||x+y||≤||x||+||y|| для кахдого х и у из L. (неравенство треугольника или Минковского)

|| x|| = √(x,x)

1°) √(x,x)>0, √(Θ,Θ)=0;

2°) √( λ x, λ x)= √ λ2(x,x)=| λ|·√(x,x);

3°) √(x+y,x+y)= √(x,x)+(y,y)+(x,y)+(y,x)= √(x,x)+2(x,y)+(y,y)

Докажем, что

√(x+y,x+y) ≤√(x,x)+√(у,у)

т.к. обе части неравенства неотрицательны, возведем в квадрат: (х+у,х+у) ≤(х,х)+2√(x,x)√(у,у)+(у,у)

(x,x)+2(x,y)+(y,y) ≤(х,х)+2√(x,x)√(у,у)+(у,у)

2(x,y) ≤2√(x,x)√(у,у) (x,y) ≤√(x,x)√(у,у)

т.к. обе части неравенства неотрицательны, возведем в квадрат: (x,y)2 ≤(x,x)·(у,у)-неравенство Коши-Буяновского.

ч.т.д В любом вещественном евклидовом пр-ве можно ввести понятие угла между векторами.

42) Ортонормированный базис и его существование в евклидовом пространстве.

N векторов е1, е2, …,еn n-мерного евклидова пр-ва образуют ортонормированный базис этого пр-ва, если эти элементы попарно ортогональны и норма каждого из этих векторов =1.

Если =0 при и , то базис называется ортогональным.

Установим корректность определения, т.е докажем, что е1, е2, …,еn – ЛНЗ►◄

//Систему векторов е1, е2, …,еn линейного пространства L называют ортонормированным базисом этого пространства, если данная система векторов линейно независима, нормирована, ортогональна и любой вектор пространства L линейно выражается через векторы этой системы. Система векторов нормирована, если нормированы все ее векторы. Вектор х нормирован, если ||x||=1.

Система векторов ортогональна, если в ней все вектора попарно ортогональны.

Два ненулевых вектора ортогональны, если угол φ между ними равен

π/2, т.е. (х,у)=0.

Теорема. Во всяком n-мерном евклидовом пространстве существует ортонормированный базис.

►Доказательство. По определению n-мерного пространства в нем существует какой-то базис. С помощью процесса ортогонализации из него можно построить ортогональный базис e1,e2,…en, если каждый вектор заменить на e’k=ek/||ek||, то получим ортонормированный базис.◄

43) Докажите, что ортогональная сумма ненулевых подпространств является прямой суммой.

Докажем для S =L1L2, т.к. S =L1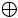L2…Ln= (L1L2) (L3 …Ln).

Доказательство. Сумма S подпространств L1,L2,…Ln называется ортогональной и обозначается S =L1L2. Каждый вектор из S по определению суммы подпространств, представляется в виде e1+e2, где e1 из L1, e2 из L2. Предположим, что какой-то вектор х из S разложен в такую сумму двумя способами:

х= e1+e2= e’1+e’2

Тогда вектор e1- e’1= e’2-e2 принадлежит одновременно L1, L2…Ln и, значит, равен нулю, откуда e1=e’1 и e2=e’2. Значит разложение единственно и S – прямая сумма.

44) Разложение n-мерного евклидова пространства на прямую сумму своего подпространства и его ортогонального дополнения.

Евклидово пространство L является прямой суммой любого своего подпространства и его ортогонального дополнения: L =L1L1┴. Поэтому каждый вектор х из L однознано представляется в виде суммы х=у+z, где х из L, у из L1 и z из L1┴. Вектор у можно назвать ортогональной проекцией вектора х на подпространство L1. Угол между вектором х и подпространством L1 – угол между векторами х и у, значит косинус этого угла равен

(х,у)/ |x||y| = (y+z, y)/ |x||y| = (y,y)/ |x||y| = |y2|/|x||y| = |y|/|x|

Рассмотрим систему линейных однородных уравнений:

а11х1+а12х2+…+а1nxn=0 а21х1+а22х2+…+а2nxn=0

…

аm1х1+аm2х2+…+аmnxn=0

Этой системе можно дать следующую геометрическую интерпретацию. В евклидовом пространстве L (в ортонормированном базисе) задано m векторов ai=(ai1,ai2,…,ain), i=1,2,…,m. Задача состоит в том, чтобы найти все векторы х=(х1,х2,…хn), ортогональные каждому из векторов а1,

а2,…,аm.

Пусть ранг матрицы А=[aik] равен r. Если вектор х ортогонален ко всем векторам аi, то он ортогонален и к порожденному ими r-мерному подпространству L1. Таким образом векторы-решения х образуют ортогональное дополнение L1┴ подпространства L1.

Размерность L1┴. (т.е. максимальное число линейно независимых решение системы) равна n-r. Каждая фундаментальная система решений уравнений системы – это базис подпространства L1┴.

45) Нахождение по наклонной ее ортогональной проекции и перпендикуляра.

Любой вектор из евклидова пространства L всегда можно представить, причем единственным образом, в виде х=g+h, где

х-наклонная, g-ортогональная проекция, h-перпендикуляр. Задача. Найти g и h, опущенный из х на подпространство L, порожденное векторами у1 и у2...yn.

Решение. Система векторов у1, у2…yn образует базис подпространства L. Так как g из L, то

g= a1у1 + a2у2+…+anyn. Отсюда h=x- a1у1 - a2у2-…-anyn. Так как h

перпендикуляр, то

(h, y1)=0 (x, y1)- a1(у1,y1)-…- an(yn, у1 )=0

Решив данную систему уравнений, находим a1, a2…an.

h=x- a1у1 - a2у2-…-anyn находим h.

Находим g=x-h.

46) Изоморфизм n–мерных евклидовых пространств.

Два евклидовых пространства L и L’ называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие x↔x’ (x из L, x’из L’) так, что:

1°) Если x↔x’ и y↔y’ , то x+y↔x’+y’, т.е. если вектору x из L соответствует вектор x’ из L’, а вектору e из L соответствует вектор y’ из L’ , то сумме x+y соответствует сумма x’+y’.

2°) Если x↔x’, то λ x↔ λ x’.

3°) Если x↔x’ и y↔y’, то (x,y)=(x’,y’), т.е. скалярные произведения соответствующих пар векторов равны между собой.

Теорема. Все евклидовы пространства данной размерности изоморфны между собой.

Доказательство. Докажем, что все n-мерные евклидовы пространства изоморфны специально выбранному ``стандартному'' n-мерному пространству. Тем самым будет доказано, что все n-мерные евклидовы пространства изоморфны между собой.

В качестве такого стандартного n-мерного пространства мы возьмем пространство, в котором вектор определяется как совокупность действительных чисел x’=(ξ1,ξ2,…ξn), а скалярное произведение векторов x’=(ξ1,ξ2,…ξn) и y’=(η1,η2,…ηn) задается формулой (x’,y’)= ξ1

η1+ξ2 η2+…+ξn ηn

Пусть нам дано какое-либо n-мерное евклидово пространство ; выберем в нем нормированный ортогональный базис e1,e2,…en. Поставим в соответствие вектору

x= ξ1 e1+ξ2 e2+…+ξn en

совокупность n чисел , т.е. вектор x’=(ξ1,ξ2,…ξn) из R’ Покажем, что установленное соответствие есть изоморфизм. Это соответствие взаимно однозначно. Нужно проверить, что выполнены условия 1°-3° определения изоморфизма.

1°) x+y= ξ1 e1+ξ2 e2+…+ξn en+ η1 e1+η2 e2+…+ηn en= e1(ξ1+ η1)+ e2(ξ2+ η2)+…+ en (ξn+ ηn)

x’+y’= (ξ1+ η1, ξ2+ η2,…ξn+ ηn)-выполняется. 2°) λх= λ ξ1 e1+ λ ξ2 e2+…+ λ ξn en

λ х’=( λ ξ1, λ ξ2,… λ ξn)-выполняется

3°) Пользуясь формулой для скалярного произведения в ортонормированном базисе, имеем:

(x,y)= ξ1 η1+ξ2η2+…+ξn ηn

C другой стороны, по определению скалярного произведения в пространстве имеем:

(x’,y’)= ξ1 η1+ξ2η2+…+ξn ηn

Таким образом, (x,y)=(x’,y’) т.е. равенство скалярных произведений доказано.

ч.т.д

.

47) Определение унитарного пространства. Примеры унитарных пространств.

Комплексное линейное пространство называется унитарным, если x, y U поставлено в соответствие комплексное число, называемое скалярным произведением, причѐм выполнены:

λ C

Следствия из аксиом скалярного произведения:

1)

2)

Пример U:

Примером унитарного пространства является

(док-во справедливости аксиом скал произв в вопросе 48)

48) Докажите что в любом конечномерном комплексном линейном пространстве можно ввести скалярное произведение.

Рассмотрим конечномерное линейное комплексное пространство L . Пусть в данном пространстве имеется базис e1, e2 ,..., en . Тогда 2 вектора x и y из этого пространства могут быть записаны следующим образом:

сопряжение).

Покажем, что скалярное произведение, введенное таким образом, будет удовлетворять всем аксиомам скалярного произведения.

1. (x, y) ( y, x) x, y L

Имеем

По свойствам комплексных чисел (т.к. , j , j C , j 1, n т.к. множество комплексных чисел является полем) то по аксиоме В2 поля

C

49)Докажите, что всякое унитарное пространство является нормированным, если

нормированным пространством, т.е. в нѐм будут выполняться аксиомы

понятие ортогонализации остаѐтся: 2 вектора ортогональны, если (х, у)

=

0.

50)Свойства ортонормированного базиса в унитарном пространстве.

Ортонормированным базисом U называется совокупность векторов , удовлетворяющая условию:

Свойства ортонормированного базиса:

Пусть произвольный ортонормированный базис E, х и у два произвольных вектора этого пространства. Найдѐм выражение скалярного произведения (x, y) через координаты векторов х и у в базисе

.

В ортонормированном базисе скалярное произведение 2х любых векторов равно сумме произведений соответствующих координат этих

ортонормированного базиса равны скалярным произведениям на соответствующие базисные векторы.

51)Докажите, что все унитарные пространства одной размерности изоморфны между собой.

Возьмѐм 2 произвольных унитарных пространства U и U' одинаковой размерности. Они изоморфны как линейные пространства.

Если в каком-либо конкретном n-мерном U' доказана теорема, сформулированная в терминах операций "+", "*λ" и скалярного произведения, то эта теорема справедлива и в совершенно произвольном n-мерном U.

52) Процесс ортогонализации Грама-Шмидта.

От любой линейно независимой системы векторов евклидова пространства можно перейти к ортогональной системе

, состоящей из ненулевых векторов. Такой переход совершается с помощью процесса ортогонализации Грама-Шмидта по следующим формулам:

;

;

…

,;

;

Экзаменационные вопросы по курсу «Геометрия и алгебра» (первый семестр):

1Определение поля. Следствия из аксиом поля. Примеры полей. 1

2Определение комплексных чисел. Поле комплексных чисел.1-2-3

3Алгебраическая и тригонометрическая формы записи комплексных чисел.3 Покажите, что

4. Сопряженные комплексные числа. Покажите, что 4

; ; ; ; α·.

5.Основные операции над матрицами и их свойства. 4-5

6.Определение и свойства определителей. 5-6

7.Вычисление определителей второго и третьего порядков. 6

8.Разложение определителя по строке (столбцу).6-7

9.Теорема Лапласа. 7

10.Докажите, что сумма произведений элементов какого-либо столбца (строки) на 7-8

алгебраические дополнения элементов другого столбца (строки) равна нулю.

11.Докажите, что алгебраическое дополнение Aij элемента aij связано с 8 минором Mij соотношением Aij=(-1)i+j*Mij

12.Обратные матрицы, их вычисление.8-9

13. Решение СЛАУ с невырожденной основной матрицей по формулам Крамера.9-10

14.Определение линейного пространства. Свойства линейных пространств. Примеры линейных пространств.10

15.Линейные комбинации, линейная зависимость. Докажите, что система векторов е1,е2,…,еn линейно независима тогда и только тогда, когда из равенства α1e1+α2e2+…+αnen= следует

равенство нулю всех коэффициентов линейной комбинации. 10-11-12

17.Докажите, что элементарные преобразования системы векторов не нарушают ее линейную зависимость или независимость. 12-13

18.Эквивалентные системы векторов. Докажите, что если каждый из векторов линейно

независимой системы х1,х2,...,хm линейно выражается через векторы другой системы у1,у2,...,уn, то m. Докажите, что

эквивалентные линейно независимые системы состоят их одного и того же числа векторов. 13-14

независимых векторов f1,f2,.., fk (k < п) можно дополнить до базиса n-мерного пространства L. 14 21. Понятие подпространства и линейной оболочки. Примеры подпространств.

14-15

22. Сумма и пересечение подпространств. Докажите, что для любых двух подпространств L1 и L2 15-16конечномерного пространства L имеет место равенство:dim(L1 L2) + dim(L1+L2) = dimL1 +

dimL2.

23. Прямая сумма подпространств. Докажите, что для того чтобы пространство L было прямой суммой своих подпространств L1, L2, …, Lm , необходимо и достаточно, чтобы объединение базисов этих подпространств составляло базис всего подпространства .16-17 24)Докажите, что для того чтобы сумма двух линейных подпространств было прямой суммой, необходимо и достаточно, чтобы пересечение этих подпространств было нулевым. 17

25.Изоморфизм линейных пространств. Докажите, что все конечномерные пространства, заданные над одним полем, изоморфны, если и только если они имеют одинаковую размерность. Пример изоморфных линейных пространств.17-18

26.Докажите, что всякое n-мерное векторное пространство L над полем F изоморфно Fn. 18

27.Ранг матрицы, базисный минор. Докажите, что любая строка (любой столбец) матрицы А является линейной комбинацией базисных строк (базисных столбцов). 18-19

28.Докажите, что определитель равен нулю тогда и только тогда, когда между его строками

(столбцами) существует линейная зависимость. 19 29. Докажите, что размерность линейной оболочки системы векторов-столбцов матрицы

А равна рангу матрицы А; базис указанной линейной оболочки образуют базисные столбцы матрицы А. 19

30.Докажите, что ранг любой матрицы равен максимальному числу линейно независимых столбцов (строк). 19

31.Докажите, что максимальное число линейно независимых строк любой матрицы совпадает с максимальным числом линейно независимых столбцов.20

32.Докажите, что однородная СЛАУ нетривиально совместна тогда и только тогда, когда ранг матрицы А меньше числа неизвестных. 20

33.Критерий Кронекера-Капелли совместности неоднородной СЛАУ. 20

34 Докажите, что множество всех решений однородной СЛАУ с n неизвестными образует подпространство размерности n-r, где r-ранг

матрицы системы. 20 35. Фундаментальная система решений однородной СЛАУ. 20-21

36 Докажите, что сумма частного решения неоднородной СЛАУ и общего решения соответствующей однородной системы дает общее решение неоднородной системы. 21

37.Определение евклидова пространства. Примеры евклидовых пространств. 21

38.Неравенство Коши-Буняковского для евклидова пространства.21-22

39.Докажите, что неравенство Коши-Буняковского обращается в равенство тогда и только тогда, когда векторы х и у коллинеарны.22

40.Докажите, что в любом конечномерном действительном линейном пространстве можно ввести скалярное произведение.22

41.Нормированное пространство. Докажите, что всякое евклидово пространство является

42.Ортонормированный базис и его существование в евклидовом пространстве.22-23

43.Докажите, что ортогональная сумма ненулевых подпространств является прямой суммой.23

44.Разложение n-мерного евклидова пространства на прямую сумму своего подпространства и его ортогонального дополнения. 23

45.Нахождение по наклонной ее ортогональной проекции и перпендикуляра. 23-24

46.Изоморфизм n-мерных евклидовых пространств. 24

47.Определение унитарного пространства. Примеры унитарных пространств. 24-25

48.Докажите, что в любом конечномерном комплексном линейном пространстве можно ввести скалярное произведение.25

49.Докажите, что всякое унитарное пространство является нормированным, если

. 25-26

50.Свойства ортонормированного базиса в унитарном пространстве.26

51.Докажите, что все унитарные пространства одной размерности изоморфны между собой. 26

52.Процесс ортогонализации Грама-Шмидта. 26