3Линейка / Экзамен / I семестр теория

вектор z есть линейная комбинация векторов х1,…, хr, а каждый из них в свою очередь, есть линейная комбинация векторов у1,…, уs , то и вектор z может быть представлен какr линейная комбинация векторов у1,…, уs.

Доказательство: Пусть z = ∑ i хi (l) , и кроме того, для всех номеров i, 1ir, хi = ∑γij yj i=1

Где i и γij - какие-то числа и поля F.

Подставляя в выражение для хi в правую часть (l) и используя соответствующие свойства

конечных сумм, получаем:

Где коэффициенты означают ξi такие выражения:

остальные. Пусть это будет e1, тогда во всей линейной комбинации a 1e1 + … + a n en мы можем построить e1 = 2e2 + … + nen и произвольная линейная комбинация векторов e1, e2 ,…, en представима соответственно комбинацией векторов e2,…, en . Если среди векторов e2,…, en некоторый

векторn , например, e2 снова линейно выражается через остальные, то повторяя рассуждения получим, что любая линейная комбинация векторовi=1 e1,…, en является линейной комбинацией e3,…, en . Продолжая этот процесс перейдем от системы e1,…., en к системе векторов, из которой уже нельзя исключить ни одного вектора.

Линейная оболочка новой системы будет совпадать с линейной

оболочкой векторов e1,…, en. Кроме того, если среди векторов e1,…, en был хотя бы один ненулевой вектор, то новая система векторов либо состоит

только из одного ненулевого вектора, либо никакой из ее векторов не выражается линейно через остальные. Такая система называется линейно независимой.

Если система векторов не является линейно независимой, то она линейно зависимая. Система, состоящая только из нулевого вектора,

s

будет линейно зависима.

Лемма 1: Если не все векторы из системы e1,…,en нулевые и эта система линейноj=1 зависима, то в ней можно найти линейно независимую

подсистему, линейная оболочка которой совпадает с L (e1,…, en). Доказательство приведено выше.

Лемма 2: Если некоторая подсистема векторов системы e1,…, ek линейно зависима, то вся система линейно зависима. Доказательство: Не ограничивая общность рассуждений, можно считать, что линейно зависимыми являются первый вектор e1, e2 ,…, ek => существуют такие a

1,…,a k среди которых есть не равные 0, что a1e1+ a2e2+…+ akek = θ

a1e1+ a2e2+…+ akek +0ek+1 +…+ 0en = θ => имеем линейную комбинацию e1,…, en= θ, а коэффициенты не все равны нулю => лемма доказана. Лемма 3: Если среди векторов e1,…, en есть хотя бы один нулевой вектор, то вся система линейно зависима. Доказательство: Действительно, система, состоящая из одного нулевого вектора линейно зависима, то и вся система линейно зависима по лемме 2.

Лемма 4: Для того чтобы линейные оболочки L (x1, x 2 ,…, x m) и L (у1, у 2 ,…, у n) совпадали необходимо и достаточно, чтобы эти системы были эквивалентны.

Доказательство: 1) Необходимость: Пусть L (x1, x 2 ,…, x m) = L (у1, у 2 ,…, у n) Данной линейной оболочке заведомо принадлежит каждый из векторов обеих систем, кроме того, всякий вектор из линейной оболочки может быть представлен в виде линейной комбинации либо х, либо у => система векторов (x1, x 2 ,…, x m) ~ системе векторов (у1, у 2 ,…, у n)

2) Достаточность: Пусть система векторов (x1, x 2 ,…, x m) ~ системе векторов (у1, у 2 ,…, у n), тогда в силу транзитивности понятия линейного

комбинирования, всякая линейная комбинация векторов одной системы может быть представлена линейной комбинацией векторов другой

системы, т.е. L (x1, x 2 ,…, x m) = L (у1, у 2 ,…, у n)

(Т1)Система векторов e1,…, en линейно независима тогда и только тогда, когда из равенства a1·e1+ a2·e2+…+ an·en = θ следует равенство нулю всех коэффициентов линейной комбинации.

Доказательство: 1) Необходимость: Система e1,…, en линейно независима. Предположим, что равенство нулю линейной комбинации, возможно при некотором наборе коэффициентов, среди которых есть хотя бы один, отличный от нуля. Пусть a1 ≠ 0 , тогда e1= (-a2 /a1)·e2+…+ (-an /a1)·en , т.е. вектор выражается через остальные, что противоречит условию независимой системы векторов.

2) Достаточность: Если равенство нулю влечет за собой равенство нулю коэффициентов a 1,…, a n , то система векторов не может быть линейно зависима. От противного. Пусть, например, e1 линейно выражается

через остальные, т.е. e1 = 2e2 + … + nen e1 +(- 2)e2 + … + (- n)en = θ

Противоречие, т.к. a1 = 0, ai = 0, 1 при е1 ≠ 0.

Эта теорема часто служит определением линейно независимой системы векторов.

16) Докажите, что система векторов e1,…, en линейно зависима тогда

пусть последний ненулевой коэффициент есть a k. Если k=1, это означает, что e1= . Если k>1, то из соотношения находим:

ek = (-a 1/ a k) e1 – (a 2/ a k) e2 - … - (a k-1/ a k) ek-1

2) Достаточность: Либо e1= , либо ek= 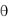=> ek = 1e1 + … + k-1e-1. Результат вытекает из леммы 3.

17) Докажите, что элементарные преобразования системы векторов не нарушают ее линейную зависимость или независимость.

Вопрос о линейной зависимости/независимости системы векторов e1, e2 ,..., en разрешается путем решения вопроса о том чему равны

коэффициенты линейной комбинации 1e1 2e2 ... nen при условии

равенства этой линейной комбинации нулю.

Если все коэффициенты будут равны нулю то система будет линейно независимой. Если же какие то коэффициенты будут не равны нулю то система будет линейно зависимой. Коэффициенты находятся путем решения однородной СЛАУ .

Рассмотрим систему e1,...., ek , ek 1..., en которой соответствует линейная

Приравнивая обе линейные комбинации к нулю получим две однородные СЛАУ для нахождения коэффициентов линейных комбинаций. Пусть вектор

Эквивалентные преобразования с матрицами СЛАУ приводят первую матрицу однородной СЛАУ ко второй. Значит решения (коэффициенты

i ) у этих СЛАУ будут совпадать. То есть заключаем что перестановка векторов системы не влияет на линейную зависимость/независимость.

Т.е. она совпала с матрицей первой системы. Значит решения этих СЛАУ совпадают. Значит умножение вектора системы на ненулевое число не влияет на линейную зависимость/независимость.

Теперь рассмотрим в качестве второй системы векторов систему

получили матрицу первой СЛАУ. Значит решения (коэффициенты i ) у этих СЛАУ будут совпадать. То есть заключаем что добавление к

вектору другого вектора умноженного на ненулевое число не влияет на линейную зависимость/независимость системы векторов.

18)Эквивалентные системы векторов.

а) Докажите, что если каждый из векторов линейно независимой системы x1,…, xm линейно выражается через векторы другой

системы y1,…,yn, то mn.

б) Докажите, что эквивалентные линейно независимые системы состоят из одного и того же числа векторов.

Пусть даны две системы векторов x1,…, xm и y1,…, yn из линейного пространства L.

Две системы векторов обладающие тем свойством, что каждый вектор в каждой системе линейно выражается через векторы другой системы, называются эквивалентными.

(Т3)Доказательство а): По условию теоремы xm линейно выражается через векторы y1,…, yn. Следовательно вся система xm, y1,…, yn линейно зависима. xm≠ . Поэтому некоторый вектор yi является линейной комбинацией предшествующих векторов. Исключив этот вектор, мы получим такую систему:

xm, y1, …, yi-1, yi+1, …, yn Используя транзитивность понятия линейной комбинации, легко показать, что каждый из векторов x1,…, xm линейно выражается через векторы новой системы. Добавим xm-1: xm-1, xm, y1,…,

yi-1, yi+1, …, yn это линейно зависимая система. Вектор xm-1≠ . Поэтому, согласно теореме 2 (о зависимой системе векторов) один из остальных

векторов системы является линейной комбинацией предшествующих векторов.

Этим вектором не может быть xm, т.к. в этом случае была бы линейно зависимой система из 2-х векторов xm-1, xm. Следовательно и вся система векторов x1,…, xm. Таким образом, некоторый вектор yk линейно выражается через предшествующие. Если мы исключим его, то опять получим систему, через которую линейно выражается каждый из векторов x1,…, xm. Продолжая этот процесс можно заметить, что y1,…, yn не могут быть исчерпаны раньше, чем мы присоединим все векторы x1,…, xm. В противном случае окажется, что некая подсистема x1,…, xm является линейной комбинацией всей системы, т.е. система x1,…, xm

линейно зависима. Поскольку это противоречит условию теоремы =>

mn

(Следствие1) Эквивалентные линейно независимые системы состоят из одного и того же числа векторов. Доказательство б): Пусть x1,…, xm и y1,…, yn - две эквивалентные системы векторов. Тогда по теореме 3

(выше описанная) имеем, что с одной стороны mn, а с другой

стороны nm, применим эту теорему в каждой системе => n=m . Следствие 2: Любые n+1 векторов из линейной оболочки систем

n линейно зависимы.

Следствие 3: Какова бы не была система одновременно не равных нулю векторов, в ней существует эквивалентная ей линейно независимая подсистема.

19)База и ранг системы векторов. Докажите, что все элементарные преобразования системы векторов приводят к эквивалентной системе.

Базой системы векторов называется эквивалентная ей линейно независимая система векторов. В общем случае база не единственна. Рангом системы векторов называется максимальное число линейно независимых векторов системы.

Элементарные преобразования системы векторов приводят к эквивалентной системе:

1) Умножение вектора на число, отличное от нуля; 2) Прибавление к любому вектору системы любой линейной комбинации остальных простых векторов; 3) Перестановка двух векторов; 4) Присоединение любой системы векторов к системе векторов; 5) Исключение из системы вектора, являющегося комбинацией простых векторов. // по умолчанию

20)Базис линейного пространства. а) Докажите, что разложение любого вектора x L по данному базису единственно. б) Докажите, что произвольную систему из k линейно независимых векторов x1,…, xk, где k<n можно дополнить до базиса n-мерного пространства

L.

Линейное пространство L называется n-мерным, если в нем существует система из n линейно независимых векторов и всякая система из большего числа векторов линейно зависима. dim L = n

Если в L существует линейно независимая система, содержащая сколь угодно большое число векторов, то линейное пространство называется бесконечномерным.

Пусть задано n-мерное пространство L, выберем линейно независимую систему с максимальным количеством векторов e1,…, en , тогда для любого x L система e1,…, en , x, будет линейно зависимым и по теореме 2 (о зависимой системе векторов) x линейно выражается через остальные векторы

x = a1·e1+ a2·e2+…+ an·en (1). Любое конечномерное линейное пространство есть линейная оболочка конечного числа своих векторов. Конечномерная система векторов x1,…, xm называется базисом линейного пространства L, если она:

1)Линейно независима

2)Через нее линейно выражается любой вектор из L

Соотношение (1) называется разложением х по базису e1,…, en , а числа a 1,…,a n - коэффициентами разложения.

Значит среди ei найдется хотя бы один вектор не являющийся линейной комбинацией векторов f1, f2 ,…, fk . Пусть таким вектором будет е1i ,добавим его в систему f1, f2 ,…, fk , в результате получим линейно независимую систему из k+1 векторов. Если k+1<n, то поступая аналогично, построим линейно независимую систему из k+2 векторов,

получим f1, f2 ,…, fk , е1i ,е2i

Будем продолжать, пока не получим базис.

Следствие: Если в каком-нибудь подпространстве L (dimL = s) выбран некоторый базис

e1, e2 ,…, es то всегда можно выбрать векторы es+1,…,еn в пространстве L

(dimL=n) так, что система векторов e1, e2 ,…, es , es+1,…,en будет базисом

L.

21) Понятие подпространства и линейной оболочки. Примеры подпространств.

Подпространством L1 линейного пространства L называется совокупность элементов из L таких, что сами они образуют линейное пространство. Относительно введенных в L операций сложения

(x+y) L1, (λx) L1

Примеры подпространств:

1) Множество векторов вида ( ,γ, ) является подпространством

Аналогично предыдущему примеру, проверим условия замкнутости сложения и умножения, получим что данное множество будет являться подпространством пространства Rnхn.

Поскольку любое подпространство само по себе является линейным пространством, то все такие понятия, как базис и т.д., применимы и к подпространствам. Так как в подпространстве не может быть больше линейно независимых векторов, чем во всем пространстве, то размерность любого подпространства не превосходит размерности всего пространства.

Линейной оболочкой L (e1,…, en) системы векторов x1,…, xn называется множество всех ее линейных комбинаций.

Зафиксируем систему e1,…, en и позволим коэффициентам линейной комбинации принимать любые значения из поля F. В результате получим некоторое множество векторов из L, которое называется линейной оболочкой векторов e1,…, en и обозначается L

(e1,…, en) = a 1e1 + … + a nen , a i Z

Она легко строится и сама является линейным пространством.

Пусть существуют числа, такие что (ax+ y)= a(∑ξi ei ) +n (∑ ηi ei) n=

Лемма 4: Для того чтобы линейные оболочки L (x1, x 2 ,…, x m) и L (у1, у 2 ,…, у n) совпадали необходимо и достаточно, чтобы эти системы были эквивалентны.

Доказательство: 1) Необходимость: Пусть L (x1, x 2 ,…, x m) = L (у1, у 2 ,…, у n) Данной линейной оболочке заведомо принадлежит каждый из векторов обеих систем, кроме того, всякий вектор из линейной оболочки может быть представлен в виде линейной комбинации либо х, либо у => система векторов (x1, x 2 ,…, x m) ~ системе векторов (у1, у 2 ,…, у n)

2) Достаточность: Пусть система векторов (x1, x 2 ,…, x m) ~ системе векторов (у1, у 2 ,…, у n), тогда в силу транзитивности понятия линейного комбинирования, всякая линейная комбинация векторов одной системы может быть представлена линейной комбинацией векторов другой

системы, т.е. L (x1, x 2 ,…, x m) = L (у1, у 2 ,…, у n)

22) Сумма и пересечение подпространств. Докажите, что для любых

Подпространством L1 линейного пространства L называется совокупность элементов из L таких, что сами они образуют линейное пространство. Относительно введенных в L операций сложения векторов и умножения вектора на число. Другими словами L1 L является подпространством, если из того, что x и y L1 следует, что

(x+y) L1, (λx) L1

Суммой (L1+L2) подпространств называется множество векторов z вида: z=x+y, где x L1, y L2, z L. Пересечением подпространств (L1 L2)

L1∩L2 – подпространство, выберем в нем базис с1,с2,…,сm. Эти векторы л.н.з. и лежат в L1. Согласно лемме (если в каком-то подпр-ве L (dimL=s) выбран базис е1,е2,…,еs , то всегда можно выбрать векторы

еs+1,еs+2,…,еn в пр-ве L (dimL=n) так, что система векторов е1,е2,…,еs , еs+1,еs+2,…,еn будет базисом во всем линейном пространстве L.) найдутся

такие векторы а1,а2,…,ак , что система а1,а2,…,ак, с1,с2,…,сm ,,будет базисом в L1.

Аналогично, в подпространстве L2 найдутся такие векторы b1, b2, . . . ,bp, что система b1, b2, . . . ,bp, с1,с2,…,сm будет базисом в L2. При этом

r1=k+m, r 2 = р + т.

Всякий вектор из подпространств L1,L2 линейно выражается через векторы своего базиса и тем более линейно выражается через векторы

(2). Поэтому через эти векторы будет линейно выражаться и любой вектор из суммы L1 + L2. Нам остается показать, что система (2) линейно независима. Пусть

α1a1+…+ αkak +γ1c1+…+γmcm+…+β1b1+…+βpbp= 0. (3)

для некоторых чисел ν1,…,νm. Сравнивая (4), (5), получаем

β1b1+…+βpbp + (-ν1)c1+…+(-νm)cm = 0.

Система векторов b1, b2, . . . ,bp, с1,с2,…,сm линейно независима по построению, поэтому

β1=…=βp=ν1=…=νm = 0.

В силу линейной независимости системы векторов а1,а2,…,ак, с1,с2,…,сm из (3) теперь вытекает, что

α1=…=αk=γ1=…=γm = 0.

Теорема доказана.◄

23. Прямая сумма подпространств. Докажите, что для того чтобы пространство L было прямой суммой своих подпространств L1, L2,

…, Lm , необходимо и достаточно, чтобы объединение базисов этих подпространств составляло базис всего подпространства.

Пусть имеем такие подпространства L1, L2, …, Lm некоторого линейного пространства L, что L=L1+L2+…+Lm, (1) т.е. вектор x L представим как x=x1+x2+…+xm (2) xi L

Вобщем случае такое представление вектора не единственно, если

xL допускается единственное представление (2), то сумма (1)

называется прямой суммой и обозначается L=L1+˙L2+˙…+˙Lm (*) Таким образом 2 справедливо, если:

1) x L существует разложение

x = x1+…+xm , xi Li , i=1,m

2) Это разложение единственно

x = x1+…+xm x = y1+…+ym, xi = yi

Для того, чтобы пространство L было прямой суммой своих подпространств L1,…, Ln необходимо и достаточно, чтобы объединение базисов этих подпространств составляло базис всего подпространства. ►Необходимость

Пусть K есть прямая сумма подпространств L1,..,Lm т векторы

e1,…,eS1;…; eS(m-1)+1,.., eS(m) составляют базисы этих подпространств. Тогда для любого вектора x из K имеет место разложение (2).

Представив каждый из векторов xi в виде разложения по базису соответствующего подпространства Li, полчим, что

x=α1e1+…+αS1eS1+…+αS(m-1)+1e S(m-1)+1+…+αSmeSm=0 (4)

для некоторых чисел α1, …, αSm.

Таким образом, каждый вектор из К можно представить в виде линейной комбинации векторов е1, ..., еSm . Для того чтобы утверждать, что эти векторы составляют базис пространства К, остается доказать их линейную независимость. Рассмотрим равенство

βS(m-1)+1e S(m-1)+1+…+βSmeSm=ym.

Очевидно, что yi€Li , а из (5) следует такое равенство:

0=y1+…+ym.

Все подпространства содержат нулевой вектор, поэтому заведомо справедливо соотношение

0 = 0 + . . . + 0.

В силу единственности разложения нулевого вектора из К по подпространствам L1,…,Lm заключаем, что

y1=…=ym=0.

Отсюда вытекает равенство нулю всех коэффициентов линейных комбинаций (6), т. е. линейная независимость векторов e1,…, eS(m) .

Достаточность

Предположим теперь, что векторы e1,…,eS1;…; eS(m-1)+1,.., eS(m), составляющие базисы подпространств L1,..,Lm, образуют базис К. Тогда

для любого вектора х из К имеет место единственное разложение (4). Обозначив

α1e1+…+αS1eS1=x1,

…………………. (7)

αS(m-1)+1e S(m-1)+1+…+αSmeSm=xm,

мы получим, что для х существует по крайней мере одно разложение (2). Каждый вектор xi из (7) есть линейная комбинация базисных векторовLi. В силу единственности разложения (4) для вектора х заключаем и о единственности для него разложения (2). Теорема доказана.

◄

24)Докажите, что для того чтобы сумма двух линейных подпространств было прямой суммой, необходимо и достаточно, чтобы пересечение этих подпространств было нулевым.

1)необходимость:

От противного: допустим что пересечение содержит не только нулевой вектор. Пусть это вектор z.

Тогда z представим в виде: z=0+z=z+0, что противоречит определению прямой суммы. Значит предположение неверно и пересечение пространств – только нулевой вектор.

2)достаточность: пусть L=L1+L2 и пересечение L1 и L2={0}.каждый вектор баз пространств L1 и L2 есть в L по определению суммы пространств. вместе с тем система из объединения баз пространств ЛНЗ (так как пересечение пространств – только нулевой вектор) и является базой L(любой вектор L выражается через лин.комбинацию векторов объединенной базы).по теореме 7 (для того чтобы пространство L было прямой суммой своих подпространств L1, L2, …, Lm , необходимо и достаточно, чтобы объединение базисов этих подпространств составляло базис всего подпространства)– сумма L1 и L2 – прямая.

25) Изоморфизм линейных пространств. Докажите, что все конечномерные пространства, заданные над одним полем, изоморфны, если и только если они имеют одинаковую размерность. Пример изоморфных линейных пространств.

Пространства, устроенные одинаково по отношению к операциям сложения векторов и умножения вектора на число будем считать обладающими одинаковыми свойствами или изоморфными.

Два линейных пространства L и L’ заданные над одним и тем же полем F называются изоморфными, если между векторами x L и x' L' можно установить взаимно-однозначное соответствие введением некоторой «функции», то есть x'=ω(x), «аргументом» которой является вектор пространства K, а «значением» - вектор x' из пространства K'. Теперь оба свойства этой функции можно записать следуюшим образом. Для любых x, y из K и любого числа λ

ω(x+y)=ω(x)+ω(y), ω(λx)=λω(x).

1)(x+y) <-> (x'+y')

2)(x+y)'<-> x'+y'

3)λx <-> λx'

4)(λx)'<->λx'

Свойства изоморфизма: L<->L'

1) При изоморфизме L переходит в ' L'

ω(0)=ω(0·x)=0·ω(x)=0·x'=0'

2)Линейно независимая система векторов в L переходит в линейно независимую систему векторов в L’

Теорема изоморфизма: Все конечномерные пространства, заданные над одним и тем же полем, изоморфные если и только если они имеют одинаковую размерность.

► Пусть К и К' - два произвольных линейных пространства размерности п. Выберем какой-либо базис e1, e2,.., en в пространстве К и базис e1', e2',.., en ' в пространстве К'. С помощью этих систем векторов построим следующим образом изоморфизм ω. Каждому вектору

x=α1e1+α2e2+…+αnen

пространства К поставим в соответствие вектор

ω(х) = α1e1'+α2e2'+…+αnen'

пространства К'. Установленное соответствие будет взаимно однозначным, так как разложение по базису единственно.

Возьмем, далее, два любых вектора х и у из К и произвольное число λ и предположим, что

x= α1e1+α2e2+…+αnen y= β1e1+β2e2+…+βnen

Имеем

ω(x+y)=ω((α1+β1)e1+(α2+β2)e2+…+( αn+βn)en)= =(α1+β1)e1'+(α2+β2)e2'+…+( αn+βn)en'=

=( α1e1'+α2e2'+…+αnen')+( β1e1'+β2e2'+…+βnen')=ω(x)+ω(y),

ω(λx)=ω((λα1)e1+(λα2)e2+…+(λαn)en)= =(λα1)e1'+(λα2)e2'+…+(λαn)en'= =λ( α1e1'+α2e2'+…+αnen')=λω(x).

Полученные равенства и доказывают справедливость утверждения теоремы.◄

Рассмотрим пространство комплексных чисел С. И рассмотрим

комплексное число a ib и наоборот с одними и теми же a, b R . Легко

можно убедиться в том что сумме функций соответствует сумма комплексных чисел. А функции умноженной на рациональное число соответствует комплексное число умноженное на то же самое рациональное число. Таким образом эти 2 пространства изоморфны между собой.

26)Докажите, что всякое n-мерное векторное пространство L над полем F изоморфно Fn.

L – линейное пространство над полем F;

dimL=n;

Fn – линейное пространство над полем F; dimF=n;

значит по теореме (все конечномерные пространства одинаковой размерности, заданные над одним и тем же полем, изоморфны) => L и Fn изоморфны.

27)Ранг матрицы, базисный минор. Докажите, что любая

строка(любой столбец) матрицы А явл. Линейной комбинацией базисных строк(базисных столбцов).

Будем рассматривать различные миноры k-го порядка, т.е. определитель подматриц, образованных из элементов стоящих на пересечении k-строк и k-столбцов матрицы k<=min (n,m)

Предположим, что хотя бы один элемент ij матрицы A отличен от нуля. Рангом матрицы A называется такое натуральное число r, что:

1)Матрица A имеет минор порядка r не равный нулю

2)Всякий минор (r+1)-го порядка матрицы A равен нулю Если A – нулевая, то rgA=0

Отличный от нуля минор порядка r называется базисным минором A. Строки (столбцы), на которых построен базисный минор, называются базисными.

Любой столбец (строка) матрицы A является линейной комбинацией ее базисных столбцов (базисных строк).

►Поскольку при произвольных переменах столбцов (или строк) определитель сохраняет свойства равенства нулю, можно не ограничивая общности считать, что базисный минор расположен на первых r строках и столбцах матрицы A, где r=rgA.

Рассмотрим определитель порядка (r+1)

Определить D по последней строке

αk1Ak1+αk2Ak2+…+αkrAkr+αksAks=0 (1)

где Ak1, Ak2,…,Akr,Aks – алгебраические дополнения элементов αk1, αk2,…, αkr, αks соответственно

Заменим Aki на Ci для всех i=

Учитывая, что Cs , т.к. алгебраические дополнения Aks образуются базисным минором, мы можем поделить каждое из полученных

равенств на Cs и выразим α1s, α2s,…, αns из системы: Обозначение λj=- ,

j=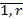

α1s=λ1α11+λ2 α12 +…+λr α1r , α2s=λ1α21+λ2 α22 +…+λr α2r ,

…

αns=λ1αn1+λ2 αn2 +…+λr αnr ,

sыйстолбец матрицы A является линейной комбинацией первых r столбцов (базисных).

Если один из столбцов определителя D является линейной комбинацией других его столбцов, то определитель D=0.

Пусть qый столбец матрицы A есть линейная комбиныция iго, jго,…, kго столбцов с коэффициентами λi, λj,…, λk, тогда вычитая из qго столбца iый, jый,…, kый столбцы, умноженные на λi, λj,…, λk соответственно, мы не изменим определителя D, но при этом qый столбец станет нулевым.

=>D=0◄

28)Докажите, что определитель равен нулю тогда и только тогда, когда между его строками (столбцами) существует линейная зависимость

Необходимость => По теореме Т3 Если Д=0, то у него имеется столбец являющийся

линейной комбинацией других столбцов Достаточность <=

По теореме Т2 Если один из столбцов Д - линейная комбинация других, то Д=0

<

29) Докажите, что размерность линейной оболочки системы

векторов столбцов матрицы А равна рангу матрицы А. Базис указанной линейной оболочки образуют базисные столбцы матрицы А

►Пусть для определенности базисные – первые r столбцов А. Эти столбцы линейно независимы, т.к. в противном случае определитель порядка r, построенный на этих столбцах и каких либо r строках, оказался бы равен «0», т.е. «0» был бы равен базисный минор, что противоречит определению ранга.

По теореме о базисном миноре ( любой столбец(строка) является линейной комбинацией еѐ базисных) остальные столбцы как и базисные ◄

30) Докажите, что ранг любой матрицы равен максимальному числу ее столбцов, образующих линейно независимую систему.

►Пусть ранг матрицы А равен р . Возьмем столбцы, проходящие через базисный минор. Предположим, что эти столбцы образуют линейно зависимую систему. Тогда один из столбцов является линейной комбинацией других. Поэтому в базисном миноре один столбец будет линейной комбинацией других столбцов. По предложениям 14.15(Если одна из строк матрицы является линейной комбинацией других ее строк, то определитель матрицы равен нулю) и 14.18(Все свойства определителя, сформулированные для строк, справедливы и для столбцов) этот базисный минор должен быть равен нулю, что противоречит определению базисного минора. Следовательно, предположение о том, что столбцы, проходящие через базисный минор, линейно зависимы, не верно. Итак, максимальное число столбцов, образующих линейно независимую систему, больше либо равно р.

Предположим, что р+1 столбцов образуют линейно независимую систему. Составим из них матрицу В. Все миноры матрицы В являются минорами матрицы А. Поэтому базисный минор матрицы имеет порядок не больше р. По теореме о базисном миноре, столбец, не проходящий через базисный минор матрицы В, является линейной комбинацией столбцов, проходящих через базисный минор, то есть столбцы матрицы В образуют линейно зависимую систему. Это противоречит выбору столбцов, образующих матрицу. Следовательно, максимальное число столбцов, образующих линейно независимую систему, не может быть больше р. Значит, оно равно р, что и утверждалось.

◄

31) Докажите, что максимальное число линейно независимых строк любой матрицы совпадает с максимальным числом линейно независимых столбцов.

►По теореме Ранг матрицы равен максимальному числу ее столбцов, образующих линейно независимую систему и свойству неизменности ранга матрицы при транспонировании получаем, что строки становятся столбцами и максимальное число их линейно независимых равно рангу матрицы, а соответственно и совпадает с максимальным числом линейно независимых столбцов.

◄

32) Докажите, что однородная СЛАУ нетривиально совместна тогда и только тогда, когда ранг матрицы А меньше числа неизвестных

►Ах=0; а1х1+а2х2+…+амхм=0; что бы было не тривиальное решение (а1,а2,…ам) должна быть зависимой, т.к. тогда будут существовать х1,х2,…хм, не все равные «0», что а1х1+а2х2+…+амхм=0. Система (а1,а2,…ам) линейно зависима, если ранг матрицы А меньше числа м по теореме, то есть меньше числа неизвестных.

◄

33)Критерий Кронекера-Капелли совместности неОСЛАУ

НеОСЛАУ совместна тогда и только тогда, когда ранг А = рангу А1, где А1 – расширенная матрица вида: [А|b], Ах=b.

►=> Необходимость

НеОСЛАУ Совместна, следовательно b есть линейная комбинация столбцов А, соответственно: rg А = rg А1, по теореме: ( ранг матрицы равен максимальному числу независимых столбцов.), т.е.

<= Достаточность

rg А = rg А1, то m базисных столбцов А будут базисными и в А1, и по теореме о базисном миноре ( любой столбец(строка) является линейной комбинацией еѐ базисных) b – линейная комбинация базисных столбцов и соответственно некоторая комбинация всех столбцов матрицы А, т.е. система совместна.◄

34)Докажите, что множество всех решений ОСЛАУ с n неизвестными образует подпространство размерности n-r, где r – ранг матрицы системы.

Пусть Ах=0; ранг А = r; n –число неизвестных, а базисный минор располагается в верхнем левом углу А. И пусть х1 и х2 – произвольные решения.

А(β1х1+β2х2)=А(β1х1)+А(β2х2)=β1А(х1) +β2А(х2)=0;

Т.е. совокупность всех решений ОСЛАУ – подпространство линейного пространства Fn. Всякое p решений удовлетворяет всем последующим уравнениям:

Li1x1+…+Lirxr+Lip+1xr+1+…+Linxn=0 Li1x1+…+Lirxr=- Lip+1xr+1-…-Linxn

Полагая

последовательно:

Находим n-r линейно независимых решений

Покажем что всякое решение Х= ОСЛАУ есть линейная комбинация

=

Также как и линейная комбинация x0 является решением ОСЛАУ:

А

Базисные столбцы лнз системы

А это значит что нулевой вектор, и х можно представить в виде:

◄

35) Фундаментальная система решений однородной СЛАУ: