1)Поля Def: Полем наз. множество элементов F = {α ,β ,γ ,…} для которых определены 2 алгебраические операции: сложение и умножение, так что сумма и произведение двух любых элементов α, β, принадлежащих F снова принадлежат F. Причем выполнены следующие условия (аксиомы):
|
|
|
A1. α+β=β+α для |
α,β |
F (коммутативность) |
|
|
|
|||||||
|
|
|
А2. (α+β)+γ = α+(β+γ) |
для |
α,β,γ |
F(ассоциативность |
|
||||||||
сложения) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
А3. |
нулевой элемент θ, обладающий свойствами α+θ=α для α |
|||||||||||
|
F(аксиома существования нуля) |
|
|
|
|
|
|
||||||||
|
|
|
А4. |
противоположный элемент (–α): α+(-α)=θ для |
α |
F |
|||||||||
|
|
|
B1. α*β =β*α для |
α,β |
|
F |
|
|
|
|
|
|
|||
|
|
|
B2. (α*β)*γ=α*(β*γ) для |
α,β,γ F |
|
|
|
|
|
||||||
|
|
|
B3. |
единичный элемент 1 |
F 1*α =α для |
α |
F, 1≠θ |
|
|||||||
|
|
|
B4. |
обратный элемент (α-1) |
F: α*α-1 = 1 для |
α |
F, α≠θ |
||||||||
|
|
|
C1. α*(β+γ)=α*β+α*γ для |
α,β,γ F (дистрибутивность |
|||||||||||
|
|
|
умножения относительно сложения) |
|
|
|
|
|
|||||||
Операции сложения и умножения для элементов поля являются |
|||||||||||||||
алгебраическими, т.е. являются бинарными, однозначными и |
|
||||||||||||||
замкнутыми. |
|
|
|
|
|
|
|
|
|
|
|
||||
Следствия из аксиом поля: |
|
|
|
|
|
|
|
|
|||||||
1. В поле F существует единственный нулевой элемент. |
|
|
|
||||||||||||
Д-во: Пусть это не так и существует 2 нулевых элемента 1 |
и |
2 . |
|||||||||||||
|
A3 |
|
|
A1 |
A3 |
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
2 |
2 |
1 |
2 |
|
|
|
|
|
|
|
|
|
2. Для любого |
F существует единственный противоположный |
||||||||||||||
элемент ( |
) |
|
|
|
|
|
|
|
|
|
|
|
|||
Д-во: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть имеется 2 противоположных элемента ( )1 |
и ( |
)2 . тогда |
|||||||||||||
|
|
A3 |
|
A1 |
|
A4 |
|
|
A1 |
|
|
|
|
||
( |
)1 |
|
( |
)1 |
|
( |
)1 |
[ |
( |
)2 ] ( |
)1 |
|
|
|
|
A1 |
|
|
|
|
|
A2 |
|
|
|
A4 |
|
|
|
|
|
[( |
|
)2 |
] ( |
)1 |
( |
)2 |
|
( |
)1 ( |
)2 |
( |
)2 |
|
|
|
3. |
|
|
|
( |
) |
|
|
|
|
|
|
|
|
|
|
Операция вычитания обратна операции сложения. |
|
|
|
|
|||||||||||
4. |
( |
|
) |
( |
) ( |
) |
|
|
|
|
|
|
|
|
|
Д-во:
|
|
|
|
A1 |
|
|
|
A2 |
( |
) |
(( |
) ( |
)) ( |
) (( |
) ( |
)) |
|
A2 |
|
|
|
A4 |
|
A3 |
|
A4 |
|
( |
( |
)) ( |
) ( |
) ( |
) |
( |
) |
5.Существует единственный единичный элемент Существует единственный обратный элемент
6.1,
7.
Д-во:
|
|
|
df |
|
B6 |
|
B5 |
|
B8 |
B5 |
B7 |
|
|
|
|
|
( |
1 ) |
|
( 1 |
) |
( |
1 ) |
1 1 |
|
|
|
|
|
|
|
|
|
|
|||||||
8. ( |
) 1 |
1 |
1 |
|
, |
F ( |
0, |
0) |
|
|
|
||
9. |
|
F |
|
|
|
|
|
|
|
|
|
|
|
Д-во: |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
C |
|
A2 |
|
A3 |
B7 |
|
|
|
|
|
|
|
1 |
( |
1) |
(1 |
) |
1 |
|
|
|
|
|
|
|
|
|
B7 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
A4 |
|
|
|
|
|
A2 |
|
|
A4 |
|
A3 |
|
|
|
|
( |
) ( |
|
) |
( |
) |
( |
( |
)) |
|
|
Ч.т.д. |
|
|
|
|
|
|
|
|
|
|
|
||
10. ( |
) |
( 1) |
|
|
|
|
|
|
|
|
|
||
Д-во: |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
B7 |
|
|
B5 |
|
C |
|
A4 |
B5 |
Cл. |
( |
1) |
1 |
( |
1) |
|
1 |
( 1) |
(1 ( |
1)) |
|
|
||
Примеры полей:
Поле вещественных чисел R, поле комплексных чисел C, поле рациональных чисел.
2) Опр. Комплексных чисел. Поле комплексных чисел.
Комплексным числом z называется упорядоченная пара z=(a,b) действительных чисел со следующими свойствами:
1. Два комплексных числа z1 |
(a1,b1 ) и z2 (a2 ,b2 ) равны тогда и |
только тогда когда a1 a2 |
и b1 b2 |
2. |
Сумма двух комплексных чисел z1 |
(a1,b1 ) и z2 |
(a2 ,b2 ) |
|||
|
определяется следующим образом |
|
|
|||
|
z1 |
z2 |
(a1,b1 ) (a2 ,b2 ) (a1 |
a2 ,b1 |
b2 ) (х) |
|
3. |
Вычитание двух комплексных чисел z1 (a1,b1 ) и z2 (a2 ,b2 ) |
|||||
|
определяется как операция, обратная сложению. |
|
||||
|
z1 |
z2 |
(a1,b1 ) (a2 ,b2 ) (a1 |
a2 , b1 b2 ) |
|
|
4. |
Произведение двух комплексных чисел z1 (a1,b1 ) и z2 (a2 ,b2 ) |
|||||
|
определяется следующим образом: |
|
|
|||
|
z1z2 |
(a1,b1 )(a2 ,b2 ) (a1a2 b1b2 , a1b2 |
a2b1 ) (хх) |
|
||
5. |
Деление двух комплексных чисел z1 |
(a1,b1 ) и z2 |
(a2 ,b2 ) |
|||
|
определяется как операция, обратная произведению |
|||||
|
|
z1 |
|
(a1,b1 ) |
|
|
|
a1a2 |
b1b2 |
, |
a2b1 |
a1b2 |
|
при a |
2 |
b2 |
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
z |
|
|
(a ,b ) |
|
|
a2 |
b2 |
|
a2 |
b2 |
|
|
|
2 |
2 |
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
2 |
2 |
|
|
|
|
2 |
2 |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Покажем что множество комплексных чисел С является полем |
||||||||||||||||||||||
|
|
|
относительно операций сложения и умножения определенных |
||||||||||||||||||||||
|
|
|
сооотношениями (х) и (хх) |
|
|
|
|
|
|
|
|
|
|||||||||||||
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
z1, z2 |
C ( z1 |
(a1,b1 ); z2 |
|
(a2 ,b2 ) ): |
|
|
|
|
|
|
|||||||||||||
z1 |
z2 |
|
(a1 |
|
a2 ,b1 |
b2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
z2 |
z1 |
|
(a2 |
|
a1,b2 |
b1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Из этого следует z1 |
|
|
z2 |
z2 |
z1 т.к. a1 |
a2 |
|
a2 |
a1 |
и b1 |
b2 |
b2 b1 (из |
|||||||||||||
того что a1, a2 ,b1,b2 |
из поля вещественных чисел R) |
|
|
||||||||||||||||||||||
2. |
|
z1, z2 , z3 |
C ( z1 |
(a1,b1 ); z2 |
(a2 ,b2 ); z3 |
(a3 ,b3 ) ): |
|
|
|||||||||||||||||
(z1 |
z2 ) z3 |
|
(a1 |
|
a2 ,b1 |
b2 ) (a3 ,b3 ) ((a1 |
|
a2 ) a3 ,(b1 |
b2 ) b3 ) |
||||||||||||||||
z1 |
(z2 |
z3 ) |
|
(a1,b1 ) (a2 |
a3 ,b2 |
b3 ) |
(a1 |
(a2 |
a3 ),b1 |
(b2 |
b3 )) |
||||||||||||||
Из этого следует (z1 |
|
|
z2 ) |
z3 |
z1 |
(z2 |
z3 ) |
т.к. |
|
|
|
|
|||||||||||||
(a1 |
a2 ) a3 |
|
a1 |
|
(a2 |
a3 ) и (b1 |
b2 ) b3 |
b1 |
(b2 |
|
b3 ) (из того что |
||||||||||||||
a1, a2 , a3 ,b1,b2 ,b3 |
из поля вещественных чисел R) |
|
|
|
|
||||||||||||||||||||
3. Существует нулевой элемент |
|
(0, 0) |
C такой что |
|
|
||||||||||||||||||||
z |
|
|
(a, b) |
|
(0, 0) |
|
|
(a, b) z |
|
z |
|
(a, b) |
C |
|
|
|
|
|
|||||||
4. |
z |
(a, b) |
C существует противоположный элемент |
|
( |
z) |
( |
a, b) |
C такой что |
z |
( |
z) |
(a, b) |
( a, b) (a a, b b) (0, 0) |
B
1. z1, z2 C ( z1 (a1,b1 ); z2 (a2 ,b2 ) ):
z1z2 |
(a1,b1 )(a2 ,b2 ) |
(a1a2 |
|
b1b2 , a1b2 |
a2b1 ) |
|
|
|
|
|
|
|
|
|
||||||||||||
z2 z1 |
(a2 ,b2 )(a1,b1 ) (a2a1 |
|
b2b1, a2b1 |
a1b2 ) |
|
|
|
|
|
|
|
|
|
|||||||||||||
Из этого следует z1z2 |
z2 z1 |
|
т.к. a1a2 |
b1b2 |
a2a1 |
|
b2b1 и |
|
|
|||||||||||||||||
a1b2 |
a2b1 |
a2b1 |
a1b2 |
(из того что a1, a2 ,b1,b2 |
из поля вещественных |
|||||||||||||||||||||
чисел R) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. |
z1, z2 , z3 |
|
C ( z1 |
|
(a1,b1 ); z2 |
(a2 ,b2 ); z3 |
|
(a3 ,b3 ) ): |
|
|
||||||||||||||||
(z1 z2 ) z3 |
(a1a2 |
|
b1b2 , a1b2 |
a2b1 ) (a3 ,b3 ) |
|
|
|
|
|
|
||||||||||||||||
((a1a2 |
b1b2 )a3 |
(a1b2 |
|
|
a2b1 )b3 , (a1a2 |
b1b2 )b3 |
a3 (a1b2 |
a2b1 )) |
||||||||||||||||||
(a1a2a3 |
b1b2a3 |
a1b2b3 |
|
|
a2b1b3 , a1a2b3 |
b1b2b3 |
a3a1b2 |
a3a2b1 ) |
||||||||||||||||||
z1 (z2 z3 ) |
(a1, b1 ) (a2a3 |
|
b2b3 , a2b3 |
a3b2 ) |
|
|
|
|
|
|
||||||||||||||||
(a1 (a2a3 |
b2b3 ) b1 (a2b3 |
|
a3b2 ), a1 (a2b3 |
|
a3b2 ) (a2a3 |
|
b2b3 )b1 ) |
|||||||||||||||||||
(a1a2a3 |
a1b2b3 |
|
b1a2b3 |
b1a3b2 , a1a2b3 |
|
a1a3b2 |
|
a2a3b1 |
b2b3b1 ) |
|||||||||||||||||
Из этого следует (z1 |
|
z2 ) z3 |
|
z1 (z2 z3 ) |
т.к. |
|
|
|
|
|
|
|
|
|
||||||||||||
a1a2a3 |
|
b1b2a3 |
|
a1b2b3 |
|
a2b1b3 |
a1a2a3 |
a1b2b3 |
|
b1a2b3 |
b1a3b2 |
и |
|
|||||||||||||
a1a2b3 |
|
b1b2b3 |
|
a3a1b2 |
|
a3a2b1 |
a1a2b3 |
a1a3b2 |
|
a2a3b1 |
b2b3b1 |
(из того что |
||||||||||||||
a1, a2 , a3 ,b1,b2 ,b3 |
из поля вещественных чисел R) |
|
|
|
|
|
|
|||||||||||||||||||
3. Существует единичный элемент 1 |
(1, 0) |
|
C такой что |
|
|
|||||||||||||||||||||
1 z |
(1, 0) |
(a, b) |
(1 |
a 0 b,1 b |
a 0) |
(a,b) |
z |
|
|
z (a, b) |
C |
|||||||||||||||
4. |
z |
(a, b) |
C (z |
) |
существует обратный элемент z 1 |
C такой |
||||||||||||||||||||
что z |
z 1 |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Покажем, чему равен этот элемент |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
z 1 |
1 |
|
(1, 0) |
|
1 a |
0 b |
, |
a 0 |
1 b |
|
|
|
a |
, |
|
b |
|
( z ) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
z (a, b) |
|
a2 |
b2 |
|
b2 |
|
|
a2 |
|
b2 |
a2 |
b2 |
|
|||||||||||||
|
|
|
|
a2 |
|
|
|
|
|
|
||||||||||||||||
Проверим:
z |
1 |
1 (1, 0) |
|
1 a |
0 |
b |
, |
a 0 |
1 b |
|
|
|
|
a |
, |
|
|
b |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
z (a, b) |
|
a2 |
b2 |
a2 |
b2 |
|
|
a2 |
b2 |
a2 |
b2 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
z |
z 1 |
|
(a,b) |
|
a |
|
, |
|
b |
|
|
a2 |
|
|
|
|
b2 |
|
, |
|
ab |
|
|
ab |
(1, 0) 1 |
|||||
|
a2 |
|
b2 |
a2 |
b2 |
a2 |
b2 |
|
a2 |
b2 |
|
a2 |
b2 |
|
a2 |
b2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
С z1, z2 , z3 z1 (z2 z3 )
(a1 (a2 a3 ) (a1a2 a1a3 z1 z2 z1 z3 (a1a2 b1b2
C ( z1 |
(a1,b1 ); z2 |
(a2 ,b2 ); z3 |
(a3 ,b3 ) ): |
|
|
(a1, b1 ) ((a2 , b2 ) (a3 , b3 )) (a1,b1 ) (a2 a3 ,b2 |
b3 ) |
||||
b1 (b2 |
b3 ), a1 (b2 |
b3 ) (a2 |
a3 )b1 ) |
|
|
b1b2 |
b1b3 , a1b2 |
a1b3 |
a2b1 |
a3b1 ) |
|
(a1a2 |
b1b2 , a1b2 |
a2b1 ) (a1a3 b1b3 , a1b3 |
a3b1 ) |
||
a1a3 |
b1b3 , a1b2 |
a2b1 |
a1b3 |
a3b1 ) |
|
Из этого следует z1 |
(z2 |
z3 ) z1 |
z2 z1 |
z3 т.к. |
|||
a1a2 |
a1a3 |
b1b2 |
b1b3 |
a1a2 |
b1b2 |
a1a3 b1b3 и |
|
a1b2 |
a1b3 |
a2b1 a3b1 |
a1b2 |
a2b1 |
a1b3 |
a3b1 |
|
Вывод: Так для множество комплексных чисел выполнены все аксиомы поля то С – есть поле.
3) Алгебраическая и тригонометрическая формы записи комплексных чисел. Покажите что
|
|
|
|
|
|
; arg( |
) arg |
arg ; |
|
|
|
|
|
; arg |
|
arg |
arg |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
||||||||||||
В алгебраической форме комплексное число z |
(a, b) записывается в |
||||||||||||||||
виде a bi где действительное число a называется действительной частью комплексного числа z и обозначается Re z , действительное число b называется мнимой частью комплексного числа z и обозначается Im z символом i обозначено комплексное число (0,1) называемое мнимой единицей.
Если на плоскости выбрать прямоугольную систему координат Oxy то
каждое комплексное число z a bi можно изобразить радиусвектором с координатами (a, b)
Тригонометрическая форма записи комплексного числа z a bi получается при использовании формул связи декартовых и полярных координат (a r cos , b r sin ) т.е. z r(cos i sin ) При этом
полярный радиус r называется модулем комплексного числа
z (обозначается z ) полярный угол -аргументом комплексного числа (обозначается Argz ). Модуль и аргумент комплексного числа
выражаются через его действительную и мнимую части следующим образом:
|
|
|
|
|
|
|
a |
|
|
b |
r |
|
z |
|
a2 b2 |
cos |
|
sin |
|
||
|
|
|
|
|||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||
|
|
|
a2 b2 |
a2 b2 |
||||||
|
|
|
|
|
|
|
|
|
Главным значением аргумента комплексного числа z (обозначается
argz ) считают такой аргумент |
что |
если z 0 и |
0 |
||||||
если z |
0 |
|
|
|
|
|
|
|
|
|
arctg |
b |
, |
a |
0 |
|
|
|
|
|
a |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
arg z |
arctg |
b |
|
, |
a |
0, b |
0 |
|
|
a |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
arctg |
b |
|
, |
a |
0, b |
0 |
|
|
|
a |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Отметим что Argz |
arg z 2 |
k, k |
Z |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
r1 (cos |
1 |
|
i sin |
|
1 ) |
|
|
|
|
r1;arg |
1 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
r2 (cos |
2 |
|
i sin |
2 ) |
|
|
|
|
r2 ;arg |
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
r1r2 (cos( 1 |
|
2 ) i sin( |
1 |
|
2 )) |
|
|
|
|
|
|
r1r2 ;arg( |
) 1 2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
r1 |
(cos( |
|
|
) i sin( |
|
|
|
)) |
|
|
|
|
|
r1 |
;arg |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
1 |
2 |
1 |
2 |
|
|
|
|
|
|
1 |
2 |
||||||||||||||
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
|
|
r2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Таким образом отсюда с очевидностью следует: |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
arg( |
) |
|
arg |
|
arg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arg arg arg
4) Сопряженные комплексные числа. Покажите что
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
; |
|
|
; |
|
|
|
|
|
|
|
; |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Комплексное число a |
bi называется комплексно-сопряженным с |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
комплексным числом z |
|
a bi и обозначается z |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
a1 ib1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
a2 |
ib2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
a1 |
|
ib1 |
a2 |
ib2 |
|
(a1 |
a2 ) i(b1 |
b2 ) (a1 |
a2 ) i(b1 |
b2 ) |
||||||||||||||||||||||||||||||||
|
|
|
|
|
a1 |
|
ib1 |
a2 |
ib2 |
|
(a1 |
a2 ) i(b1 |
b2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
a1 |
|
ib1 |
(a2 |
ib2 ) (a1 a2 ) i(b1 |
|
b2 ) (a1 |
|
a2 ) i(b1 |
b2 ) |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
a1 |
|
ib1 |
a2 |
ib2 |
|
(a1 |
a2 ) i(b1 |
b2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(a1 |
ib1 )(a2 |
ib2 ) (a1a2 |
b1b2 ) i(a1b2 |
b1a2 ) (a1a2 |
b1b2 ) i(a1b2 |
b1a2 ) |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
(a1 |
ib1 ) (a2 |
|
ib2 ) a1a2 |
ib2a1 |
|
ib1a2 |
b1b2 |
|
(a1a2 |
b1b2 ) i(a1b2 |
b1a2 ) |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a1 |
ib1 |
|
|
|
(a1 |
ib1 )(a2 |
ib2 ) |
|
|
|
|
a1a2 |
b1b2 |
i |
b1a2 |
a1b2 |
|
|
a1a2 |
b1b2 |
|
i |
a1b2 |
b1a2 |
|||||||||||
|
|
|
|
|
|
|
|
|
a ib |
|
|
|
|
a2 |
b2 |
|
|
|
|
|
|
|
a2 |
b2 |
|
|
a2 |
b2 |
|
|
|
a2 |
b2 |
|
|
a2 |
b2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
2 |
2 |
|
2 |
2 |
|
|
2 |
|
2 |
2 |
2 |
|||||||||||
|
|
|
|
|
|
|
a1 |
|
|
ib1 |
|
(a1 |
ib1 )(a2 |
ib2 ) |
|
|
a1a2 |
|
ia1b2 |
ib1a2 |
|
b1b2 |
|
a1a2 |
b1b2 |
|
i |
a1b2 b1a2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
a ib |
|
|
|
|
a2 |
b2 |
|
|
|
|
|
|
|
a |
2 |
b2 |
|
|
|
|
a2 |
b2 |
|
|
|
a2 |
b2 |
|
||||||||||
2 |
2 |
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
2 |
2 |
|
|
|
2 |
2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
(a ib )(a ib ) |
a2 |
ia b ib a b2 |
a2 |
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
|
|
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
a2 |
b2 |
a2 |
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
1 |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Отсюда следует что
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
; |
; |
; |
|
|
|
|
|
; |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5) Основные операции матрицами и их свойства.
Def: Совокупность чисел αij F, расположенных в виде таблицы размера mxn называется матрицей.
|
11 |
12 |
... |
1n |
|
|
|
|
|||
A |
21 |
22 |
... |
2n |
, если m=n то матрицу называют |
|
|||||
|
... ... ... ... |
|
|||
|
m1 |
am2 ... |
mn |
|
|
квадратной порядка m
Матрицы А, В считаются равными, если αij=βij. i 1, n , j 1, m . Матрица
В называется произведением матрицы A на λ, если каждый элемент B получен путем умножения каждого элемента матрицы А на λ.
Свойства матриц.
1.1*A= A
2.θ*A= 0 (нулевой матрице)
3.λ*(μ*A)=(λ*μ)*A для λ, μ F
Def: Пусть А,В,С – матрицы одинаковых размеров. C=(γij) называется
суммой А и В, если выполняется условие γij=αij+βij i 1, n , j 1, m .
Свойства:
1.А+В=В+А
2.А+(В+С)=(А+В)+С
3.(А+0)=А (0-нулевая матрица)
4. -1*А= -А |
А+(-А)=0 |
5.(λ+μ)*A=λ*A+μ*A
6.λ*(A+B)=λ*A+λ*B
7.A+A=2*A
8. (–λ)*A=-(λ*A) -(A+B)=-A-B -(-A)=A
Def: Пусть есть матрица А, у которой m строк и n столбцов, и матрица В, у которой n строк и k столбцов. Для того, чтобы можно было умножать, надо чтобы число столбцов первой матрицы совпадало с числом строк второй.
Аmxn*Bnxk=Cmxk
Свойства:
1.А*В=В*А(не всегда выполнимо)
2.А*(В*С)=(А*В)*С
3.(A+B)*C=A*C+B*C
4.C*(A+B)=C*A+C*B
5.λ*(A*B)=(λ*A)*B=A*(λ*B)
Любые квадратные матрицы порядка n можно складывать, умножать и умножать на число.
Def: Квадратная матрица А называется диагональной, если все ее
|
11 |
|
... |
|
|
|
|
|
|
недиагональные элементы равны нулю, т.е. A |
|
22 |
... |
. |
|
|
|||
|
|
... |
||
|
|
|
|
... nn
Сумма и произведение диагональных матриц – снова диагональная матрица.
Def: Диагональная матрица с диагональными элементами равными единице, называется единичной и обозначается I (или E).
А*I=A=I*A
6)Определение и простейшие свойства определителей.
Пусть дана квадратная матрица А, состоящая из n строк и n столбцов. Рассмотрим всевозможные произведения n элементов матрицы, взятых по одному из каждой строки и каждого столбца. В силу того, что αij F, в котором операция умножения коммутативна, мы можем упорядочить сомножители по номерам столбцов; в результате получим произведение
вида i 1 * |
i 2 *...* |
i n (1) , в котором i1,…,in – номера строк после |
1 |
2 |
n |
перестановки сомножителей. Очевидно, что i1,…,in – некоторые перестановки чисел 1,2,..,n. Условимся брать произведение 1 со знаком «+» или «-» в зависимости от четности или нечетности числа инверсий последовательности i1,…,in.
Def: Инверсией (беспорядком) последовательности i1,…,in называют такое расположение индексов, при котором старший индекс стоит впереди младших. Число всех беспорядков последовательности обозначается N(i1,…,in).
Def: Определителем матрицы А называется сумма всевозможных произведений вида 1 со знаком (-1)N(i1,…,in).
|
|
|
11 |
12 |
... |
1n |
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|||
|
|
|
21 |
22 |
2n |
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
det A |
A |
|
|
i 1 |
* |
i 2 *...* |
i n *( 1) |
N (i1 ,...,in ) |
|||
|
... |
... ... ... |
|
||||||||
|
|
|
|
|
|
|
1 |
|
2 |
n |
|
|
|
|
|
|
|
|
i1 ,...,in |
|
|
|
|
|
|
|
n1 |
an2 ... |
nn |
|
|
|
|
|
|
Будем считать положительным направлением для строк: слева направо, для столбцов: сверху вниз. Отрезки, соединяющие два каких-либо элемента матрицы, так же могут указывать направление. А именно, будем говорить, что отрезок, соединяющий элемент αij с αkl имеет
положительный наклон, если его правый конец расположен ниже левого, и отрицательный наклон, если его правый конец выше, чем левый. Мысленно проведем все отрезки, соединяющие попарно
in n (1), имеющие отрицательный наклон. Ставим знак «+», если
число таких отрезков четно, и знак «-» в противном случае.
Свойства определителей:
|
|
11 |
21 |
... |
n1 |
|
|
|
|
|
|||
Def: AT |
12 |
22 |
... |
n2 |
, полученная из |
|
|
||||||
|
|
... ... ... ... |
|
|||
|
|
1n |
a2n |
... |
nn |
|
|
11 |
12 |
... |
1n |
|
|
|
|
|
|
|||
A |
21 |
22 |
... |
2n |
заменой строк на столбцы с теми же номерами, |
|
|
||||||
|
... ... ... ... |
|
|
|||
|
n1 |
an2 ... |
nn |
|
|
|
называется транспонированной по отношению к матрице А.
1.detA=detAT. Оба определителя состоят из одних и тех же членов,
поэтому нам достаточно доказать что одинаковые члены в определителях матриц А и АТ имеют одинаковые знаки. Очевидно, что транспонирование квадратной матрицы сводится к ее повороту на 180 градусов вокруг диагонали. Каждый отрезок с отрицательным наклоном переходит в отрезок с отрицательным наклоном, поэтому число отрезков с отрицательным наклоном, соединяющих элементы данного члена после транспонирования не изменятся. Следовательно, не изменится и знак этого члена. Поскольку знаки всех членов сохранятся, величина определителя останется прежней. Рассмотренное свойство устанавливает равноправие его строк и столбцов. Поэтому дальнейшие свойства определителей будем формулировать и доказывать только для столбцов. При этом следует помнить, что для строк они также будут иметь место.
2.Антисимметрия столбцов: под антисимметрией столбцов понимают свойство определителя менять свой знак при перестановке двух столбцов.
3.Определитель, имеющий два одинаковых столбца равен нулю. Переставляя эти одинаковые столбцы, мы не изменим
определитель, но с другой стороны, по свойству 2 он должен изменить свой знак.
4.Линейное свойство определителя. Если все элементы j-го столбца
определителя D представимы в виде αij=λ*βi+ μ*γi для всех i=1..n, то определитель D=λ*D1+ μ*D2. Причем у определителей D1 и D2 все столбцы, кроме i-го и j-го такие же, как у определителя D,а i-ый столбец в определителе D1 состоит из чисел βi, а D2 – γi
11 |
... |
1 |
1 |
... |
1n |
|
11 |
... |
1 |
... |
1n |
|
11 |
... |
1 |
... |
1n |
|
|
|
|
|
|
|
|
||||||||||
... |
... |
... |
|
... |
... |
|
... |
... |
... |
... |
... |
|
... |
... |
... |
... |
... |
n1 |
... |
n |
n |
... |
nn |
|
n1 |
... |
n |
... |
ann |
|
n1 |
... |
n |
... |
ann |
5.Общий множитель всех элементов некоторого столбца можно вынести за знак определителя. Dj(αij)=Dj(λ βi)=λ Dj(βi)
6.Если некоторый столбец определителя состоит из нулей Dj(θ)=θ.
7.Инвариантность определителя к линейной комбинации столбцов. Определитель не изменится, если к элементам одного из его столбцов прибавить соответственно элементы другого столбца, умножив на фиксированное число.
8.det (λA)= λndet(A)
7)Вычисление определителей второго и третьего порядков.
det A |
|
|
|
|
|
|
|
|
,2 ... |
|
,n ( |
1) |
N (i1 ,i2 ,..,in ) |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
i ,1 |
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
2 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i1 ...in |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
12 |
|
|
|
11 |
|
22 |
( |
1)N (1,2) |
|
|
21 |
12 |
( |
1)N (2,1) |
|
11 |
22 |
|
21 |
12 |
|
|
|
||||||
11 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
21 |
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
21 |
22 |
|
|
|
23 |
|
|
11 |
22 |
33 |
( |
1)N (1,2,3) |
|
11 |
32 |
23 |
( 1)N (1,3,2) |
21 |
12 |
33 |
( 1)N (2,1,3) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
31 |
32 |
|
|
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
32 |
13 |
( |
1)N (2,3,1) |
|
31 |
|
22 |
13 |
( |
1)N (3,2,1) |
|
31 |
12 |
23 |
( |
1)N (3,1,2) |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
11 |
22 |
33 |
11 |
32 |
|
23 |
|
21 |
12 |
|
33 |
|
21 |
32 |
13 |
|
31 |
22 |
13 |
31 |
12 |
23 |
|
|||||||
Для вычисления определителей третьего порядка также применяется правило треугольника.
На рисунке показано какие тройки берутся со знаком плюс и со знаком минус.
Т.е параллельно главной диагонали со знаком плюс и параллельно побочной диагонали со знаком минус.
8) Разложение определителя по строке (столбцу).
Минором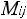 
элемента
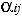определителя D n-го порядка называется
определитель
(n-1)-го порядка, получающийся из D вычеркиванием i-ой строки и k- ого столбца.
Алгебраическим дополнением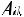 
элемента 
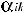называется его минор,
взятый со знаком ( 1)i |
k : |
|
= ( 1)i k |
|
|||
Рассмотрим произвольный j-ый столбец определителя D. |
|||||||
|
|
n! |
|
|
n! |
1) N (i1 ij in) = ( Все |
|
D = |
i11 i 22 inn |
= |
|
i11 ijj inn ( |
|||
|
|
i1,i 2...in |
|
i1,i 2...in |
|
||
слагаемые с |
|
|
соберем в правой части и вынесем их за |
||||
скобки, получим >>> ) = |
|
|
|
|
|||
= |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
+ … +
=
+
|
|
|
|
|
|
+ … + |
|
|
|
||||
|
|
|
|
|
||
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
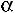
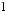
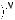
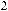
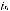
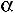
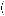
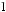
- формула разложения |
|
|
|
|
|
|
|
|
определителя по элементам j-го столбца.
9) Теорема Лапласа.
Выберем в матрице n-го порядка A элементы, стоящие на пересечении этих строк и столбцов. Они образуют квадратную матрицу k-ого порядка. Еѐ определитель назовем минором k-ого порядка и обозначим
через |
, где |
- номера выделенных строк, а |
- |
номера выделенных столбцов. Если зачеркнуть в исходной матрице выбранные строки и столбцы, то оставшиеся элементы образуют квадратную матрицу порядка n-k еѐ определитель назовем минором,
дополнительным к |
и обозначим |
Формулировка теоремы Лапласа для фиксированных номеров строк:
где i=i1+i2+…+ik; j=j1+j2+…+jk
10) Докажите, что сумма произведений элементов какого-либо столбца (строки) на алгебраическое дополнения элементов другого столбца (строки) равна нулю.
1. Пусть дан определитель D=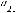 
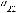
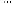
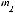
Рассмотрим
другой определитель D1, отличающийся от D лишь тем, что в k-ом его
столбце повторен i-й столбец D1=
Определитель D1 равен нулю, как определитель с двумя одинаковыми столбцами (свойство № 3: Определитель имеющий 2 одинаковых столбца равен нулю). Разложив его по элементам k-ого столбца,
получим D1 = |
, где |
- |
алгебраические дополнения элементов k-ого столбца определителя D1; но так как определитель D1 лишь k-ым столбцом отличается от D, то они будут и алгебраическими дополнениями элементов k-ого столбца определителя D. Таким образом, при всех i и k≠I
2. Пусть дан определитель D= |
Рассмотрим другой |
определитель D1, отличающийся от D лишь тем, что в k-ой его строчке повторна i-ая строчка D1=
= |
Определитель D1 равен нулю, как определитель с |
двумя одинаковыми строчками (свойство № 3: Определитель имеющий 2 одинаковых строчки равен нулю). Разложив его по элементам i-ой
строчки, получим D1 = |
, где |
- |
алгебраические дополнения элементов k-ой строчки определителя D1; но так как определитель D1 лишь k-ой строчкой отличается от D, то они будут и алгебраическими дополнениями элементов i-ой строчки определителя D. Таким образом, при всех i и k≠I
11) Докажите, что алгебраическое дополнение |
|
|
|
элемента |
|||||||||
связано с минором |
соотношением |
|
|
|
|
|
|
|
|||||
Aij=(-1)i+j * Mij |
|
|
|
|
|
|
|
|
|
|
|
|
|
Разложение по строке: det A |
i1 |
M |
i1 |
( 1)i 1 ... |
in |
M |
in |
( |
1)i n |
||||
|
|
|
|
|
|
|
|
|
|||||
Разложение по столбцу: det A |
|
M |
( 1) j 1 ... |
|
nj |
M |
nj |
( 1) j n |
|||||
|
|
|
1 j 1 j |
|
|
|
|
|
|||||
Выберем в матрице n-го порядка произвольно к строк и к столбцов. Элементы, которые стоят на пересечении этих строк и столбцов, образуют квадратную матрицу к-ого порядка. Еѐ определитель назовем
i ,...,i |
, где i1…ik – номера |
|
минором к-ого порядка и обозначим mj1 |
,..., kj |
|
1 |
k |
|
выделенных строк. Если зачеркнуть в исходной матрице выбранные строки и столбцы, то получим квадратную матрицу (n-k) порядка. Берем
определитель mi1 ,...,ik , назовем его дополнительным минором m и
j1 ,..., jk
i ,...,i |
(индексы соответствующих зачеркнутых строк / |
|
обозначим его M j1 |
,..., kj |
|
1 |
k |
|
столбцов).
►Пусть i=j=1. Соберем в правой части равенства D
= n! i11 ijj inn ( 1) N (i1 ij in) i1,i 2...in
все слогаемые, куда входят α11 и вынесем α11 за скобку, будем иметь
>>>>
α11αi22...αinn 
= 
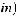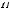
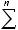
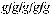αi22...αinn
= α11A11
Запишем опеределитель матрицы, получаемой из исходной после вычеркивания 1-ой строчки и 1-го столбца
|
|
Поскольку |
= |
, то |
Если i и j произвольные, то |
|
переведем путем последовательной перестановки соседних строк и
столбцов элементы 
в левый верхний угол. Для этого нам понадобиться (i-1)+(j-1)=i+j-2. Следовательно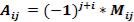 
◄
12) Обратные матрицы и их вычисления.
Пусть А – произвольная матрица размером mxn. С некоторым detA≠0. Тогда А-невырожденная или неособенная (в случае detA=0 матрица называется вырожденной или особенной), составляет присоединенную или союзную матрицу В к матрице А.
|
A11 |
A12 |
... |
A1n |
|
B |
A21 |
A22 |
... |
A2n |
. В i-той строке матрицы B находятся |
|
... ... ... ... |
|
|||
An1 An2 ... Ann
алгебраические дополнения к элементам i-ого столбца матрицы А.
Вычислим АВ.[ AB] |
[ A] [B] |
A |
|
det A,i |
j . |
n |
n |
|
|
|
|
ij |
ik kj |
ik |
jk |
0,i |
j |
k 1 |
k 1 |
|
|
AB diag(det A,..., det A)
Воспользуемся мультипликативным свойством. det(AB) = detA*detB= (detA)n=BA. Т.к. матрица А невырождена, то detB=(detA)n-1.
1
A det A B I
Def: A-1 называется обратной матрице А, если она удовлетворяет условию А*А-1=А-1*А=I
Подчеркнѐм, что обратная матрица для невырожденных матриц и
находится по формуле A 1 |
1 |
* B |
|
|
|||
det A |
|||
|
|
Не существует матрицы, обладающей свойством: det(ΑA-1)=detA det(A- 1)=detI=1
det A 1 |
1 |
|
|
||
det A |
||
|
(A-1)-1=A
Используя обратную матрицу можно находить решение СЛАУ Ax=b с невырожденной матрицей. x=(A-1)b
13) Решение СЛАУ с невырожденной основной матрицей по формулам Крамера.
Теорема 1. Сумма всех произведений элементов какого-либо столбца (строки) определителя D на соответствующее алгебраическое дополнение равна самому определителю D.
Теорема2. Сумма всех произведений элементов какого-либо столбца (строки) определителя D на соответствующее алгебраическое дополнения элементов другого столбца (строки) равно нулю.
Теорема3. (Крамера). Если матрица квадратной системы невырожденная, то система определенная.
В этом случае решение системы может быть найдено по формулам Крамера.
Пусть имеется однородная система уравнений Ax=b, b≠0, detA≠0.
11x1 |
12 x2 ... |
1n xn |
1 |
21x1 |
22 x2 ... |
2n xn |
2 |
|
... |
|
|
n1x1 |
n2 x2 ... |
nn xn |
n |
Перемножим систему на А, где А – матрица с элементами α. X- неизвестная матрица.
|
1 |
|
x1 |
|
|
|
|
|
|
||
|
|
B ... |
X ... . |
|
|
|
|
|
|||
|
|
n |
|
xn |
|
|
|
|
|
|
|
Получаем (α11A11+α21A21+…+αn1An1)x1+… |
|
|
|
|
|
|
|||||
+(α1nA11+α2nA21+…+αnnAn1)xn=β1A11+…+βnAn1 |
|
|
|
|
|
||||||
Таким образом по теоремам 1,2 имеем detA*x1 + 0*x2+…+0*xn=detA1, |
|
||||||||||
|
|
|
|
|
|
1 |
12 |
... |
1n |
|
|
|
|
|
|
|
|
|
|
||||
где А1 – матрица полученная из исходной заменой |
2 |
22 |
... |
2n |
. |
||||||
|
|||||||||||
... ... ... ... |
|||||||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
n |
n2 |
... |
nn |
|
|
|
|
|
|
|
|
|
|
||||
|
det A |
|
det Aj |
|
|
|
|
|
|
||
Значит x |
1 |
. Следовательно x |
j |
|
j=1..n. |
|
|
|
|
|
|
1 |
det A |
det A |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
Пример решения:
1. Решить с помощью формул Крамера систему уравнений x1 2x2 x3 4,
3x1 5x2 3x3 1, 2x1 7x2 x3 8.
Решение. Убедимся прежде всего в том, что определитель системы отличен от нуля:
1 |
2 |
1 |
|
3 |
5 |
3 |
1 (5 21) 2 ( 3 6) 1 (21 10) 33 . |
2 |
7 |
1 |
|
|
|
|
|
Вычислим теперь остальные, входящие в формулы Крамера,
определители: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||||
1 |
1 |
5 |
3 |
4 |
(5 |
21) |
2 |
( |
1 |
24) |
1 (7 |
40) |
33 , |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
7 |
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
4 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
3 |
1 |
3 |
|
1 ( |
1 |
24) |
4 |
( |
3 |
6) |
1 (24 |
2) |
33 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
8 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 4
3 |
3 |
5 1 1 ( 40 7) 2 (24 2) 4 (21 10) 33 . |
|
|
2 7 8
Подставив полученные значения определителей в формулы Крамера, имеем
1 |
33 |
|
2 |
33 |
|
3 |
33 |
|
||||
x1 |
|
|
|
1, x2 |
|
|
|
1, x3 |
|
|
|
1. |
|
33 |
|
33 |
|
33 |
|||||||
|
|
|
|
|
|
|
||||||
Правильность представленного решения можно проверить подстановкой значений x1 , x2 , x3 в исходную систему уравнений.
14) Определение линейного пространства. Свойства линейных пространств и примеры линейных пространств.
Линейным (или векторным) пространством на поле F называется множество элементов (векторов), которые удовлетворяют следующим аксиомам:
L={x; y; z}
A) Каждой (x,y) L ставится в соответствие элемент этого множества, называемый суммой элементов x и y (x+y) и обозначается z
1.x+y=y+x=z коммутативность.
2.(x+y)+z=x+(y+z) ассоциативность.
3. |
L: |
x L: x+ = x сущ. нуль элемента. |
|
4. |
x L: |
(-x) L |
x + (-x) = сущ. противоположного элемента. |
B) Каждой паре |
F, x L отвечает единственный элемент этого |
||
множества, называемый произведением числа *x и обозначается a= x
1. |
δ( x) = δ |
x |
δ, |
F, |
x |
L |
|
2. |
1*x = x |
x L |
|
|
|
|
|
C) Операции сложения и умножения связаны между собой |
|||||||
отношениями: |
|
|
|
|
|
||
1. |
(x+y) = |
x+ |
y |
|
F, |
x,y |
L дистрибутивность относит. |
сложения. |
|
|
|
|
|
|
|
2. |
( +λ)x = |
x+λx |
λ, |
F, |
x |
L дистрибутивность относит. |
|
множения. |
|
|
|
|
|
|
|
Из аксиом 1-8 можно вывести следующие свойства линейных |
|||||||
пространств: |
|
|
|
|
|
||
|
1) В линейном пространстве |
единственный нулевой элемент |
|||||
2)В линейном пространстве для каждого элемента x 
единственный противоположный элемент (-x)
3) Для всякого x L справедливо равенство x =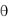 
4)Для всякого x L в любом линейном пространстве противоположным элементом служит: y=(-1)*x
Замечание:
Наличие противоположного элемента позволяет ввести операцию вычитания
x-y = x+(-y) |
|
|
||
1. |
- *x = (- )*x = |
*(-x) |
||
2. |
а) |
(x-y) = |
x - |
y |
|
б) ( |
- )*x = |
x - |
x |
3.* L = L
4. ( *x) = |
-> |
= 0F или x = |
L |
Примеры линейных пространств: |
|||
1) Fn = {x=( 1, 2, |
3, …, ) | I |
F, i=1,n} |
|
- координаты вектора x |
|
||
y = ( 1,…, n) |
i |
F |
|
Тогда: x+y = ( 1+ |
1, …, n + |
n ) |
|
λx = (λ 1, … , λ n)
Если поле вещественных чисел, то вместо Fn пишется Rn
2) Mn (R) = {f(t) = 0 + 1tn + 1t n-1 + … + n | I R }
15) Линейные комбинации, линейная зависимость. Докажите, что система векторов e1,…, en линейно независима тогда и только тогда, когда из равенства a1·e1+ a2·e2+…+ an·en = θ следует равенство нулю всех коэффициентов линейной комбинации.
Пусть дано L от поля F. Выберем конечную систему векторов и
R, где i=1,n .
Линейной комбинацией векторов e1,…,en с коэффициентами a 1,…,a n называется сумма произведений y = a 1e1+…+ a nen . При этом говорят, что y линейно выражается через векторы ei , i=1,n .
Зафиксируем систему e1,…, en и позволим коэффициентам линейной комбинации принимать любые значения из поля F. В результате получим некоторое множество векторов из L, которое называется линейной оболочкой векторов e1,…, en и обозначается L (e1,…, en) = a 1e1
+ … + a nen , a i Z
Она легко строится и сама является линейным пространством.
Доказательство: x,y L (e1,…, en), a, |
L (e1,…, en): (ax+ y) |
L (e1,…, en) |
|