Примеры

1. Найти энергии и волновые функции двух первых состояний линейного гармонического осциллятора вариационным методом.

Волновая функция основного состояния не имеет нулей и при обращается в нуль, поэтому выбираем

.

Условие нормировки

в виде

дает

.

Из (6.48)

с учетом

получаем функционал энергии

=,

.

Использовано

,

.

Из условия экстремума

находим

.

Энергия основного состояния

и волновая функция

,

совпадают с точными выражениями.

Для первого возбужденного состояния пробная функция  ортогональна четной функции ₀ . Выбираем нечетную функцию

,

автоматически обеспечивающую

.

Нормировка дает

.

Функционал (6.48)

,

.

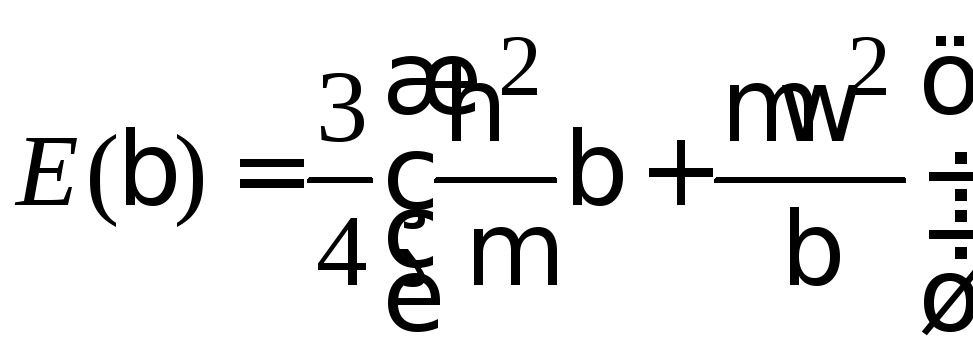Условие экстремума

дает

.

Для первого возбужденного состояния получается точный результат.

,

.

2. Доказать, что сколь угодно слабая одномерная потенциальная яма

,

имеет по крайней мере одно связанное состояние.

Функция основного состояния не имеет нулей, поэтому выбираем четную функцию, убывающую при удалении от ямы

,

где – характеризует быстроту убывания функции. Ослабление ямы означает уменьшение ее глубины, при этом функция убывает с ростом x все медленнее. Следовательно, ослабление ямы приводит к уменьшению a, и при неограниченном ослаблении . В условии нормировки

получаем интеграл Пуассона и находим

.

Для вычисления функционала энергии используем

,

,

,

тогда

.

Подставляем функцию

.

При уменьшении a первое слагаемое в скобке уменьшается, второе – увеличивается. При достаточно малом а пренебрегаем первым слагаемым, получаем

.

Согласно (6.49)

энергия не может быть меньше энергии основного состояния

.

Следовательно, основное состояние с энергией связанное.

182