ТеориЯ возмущений и диаграммы фейнмана

Фейнман разработал в 1949 г. метод интеграла по траекториям в квантовой механике и метод диаграмм. Интеграл по траекториям является аналогом метода зон Френеля в оптике – при переходе из точки А в точку В частица движется по всем возможным траекториям. Результирующая амплитуда вероятности перехода является суммой вкладов всех траекторий с учетом набега фазы на каждой из них, то есть результатом интерференции всех амплитуд.

Диаграммы Фейнмана наглядно представляют процесс, описываемый каждым порядком теории возмущений. На этой основе Фейнман разработал квантовую электродинамику. Получил Нобелевскую премию в 1965 г. Рассмотрим примеры диаграмм Фейнмана.

Ричард Фейнман (1918–1988)

Притяжение электронов сверхпроводника при обмене фононом

Сверхпроводимость. В сверхпроводнике между двумя электронами проводимости, находящимися друг от друга на расстоянии тысяч постоянной решетки, возникает сила притяжения, они двигаются взаимно согласованно и образуют куперовскую пару при низкой температуре. Взаимная согласованность приводит к тому, что электроны пары не рассеиваются на возмущениях кристаллической решетки. Сопротивление проводника обращается в нуль, возникает сверхпроводимость. Если такую согласованность имеют частицы жидкости, то возникает сверхтекучесть – отсутствие гидродинамического сопротивления.

Притяжение между электронами появляется за счет перебрасывания между ними фонона – кванта упругой волны колебаний узлов решетки. Энергия фонона

,

где  – частота волны. Опишем это явление, используя теорию возмущений, выраженную при помощи диаграмм.

Диаграмма Фейнмана изображает каждый порядок теория возмущений графически в виде процесса с участием реальных и виртуальных частиц, от лат. virtualis – способный (родиться).

Исходные и конечные состояния являются реальными частицами и изображаются сплошными линиями со стрелками, показывающими импульсы частиц.

Возмущение рассматривается как испускание, или поглощение виртуальной частицы. Такой процесс с реальной частицей запрещен законами сохранения энергии и импульса. Виртуальная частица кардинально отличается от реальной частицы. Ее характеристики – кинетическая энергия, импульс и масса не связаны обычными соотношениями:

для нерелятивистской частицы – ,

для релятивистской частицы – .

Виртуальная частица не может быть обнаружена детектором, все ее проявления косвенные. Она появляется с энергией ε на короткое время

в соответствии с соотношением неопределенностей. На диаграмме виртуальная частица изображается пунктирной линией.

Точка соединения линий – вершина диаграммы – соответствует матричному элементу оператора возмущения. В каждой вершине выполняются законы сохранения импульса и энергии. Число вершин диаграммы равно порядку теории возмущений.

Взаимодействие между электронами является обменом виртуальным фононом с импульсом q, и изображается диаграммами, показанными на рисунке. Процесс развивается во времени снизу вверх. Один электрон испускает виртуальный фонон, другой электрон его поглощает. Такие процессы допускаются законами сохранения, поскольку у виртуального фонона нет определенной связи между энергией и импульсом. Эти процессы с реальными частицами нарушают законы сохранения энергии и импульса и не возможны.

а б

Диаграммы имеют по две вершины и соответствуют второму порядку теории возмущений с поправкой к энергии (6.15)

.

Для рассматриваемых диаграмм n – исходное состояние электронов, q – виртуальное состояние, тогда энергия взаимодействия

.

Суммирование ведется по двум диаграммам и по импульсам фонона. Энергии частиц являются четными функциями импульса: для электрона , для фонона . Энергии начального и конечного состояний одинаковые:

.

а б

В области виртуальных состояний энергия

для рис. а:

,

тогда

для рис. б:

,

тогда

.

Матричный элемент взаимодействия электрона с фононом

слабо зависит от импульсов. Суммируем вклады диаграмм

.

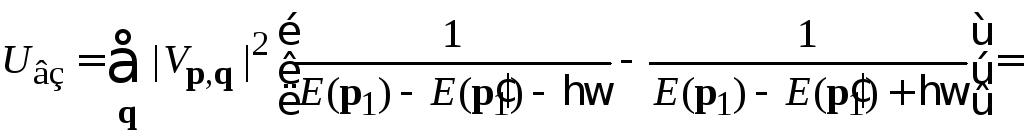
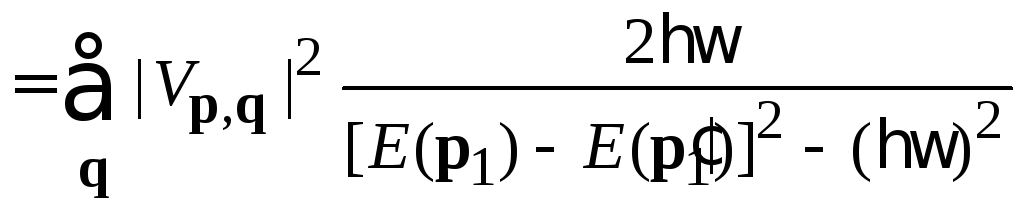При низких температурах электроны активированы в тонком слое около поверхности Ферми и изменение их энергии мало

,

тогда

.

Следовательно, при низких температурах электроны взаимно притягиваются.

Образуется коррелированно движущаяся куперовская пара электронов. Ее возникновение физически объясняется тем, что при рассеянии на неоднородностях кристаллической решетки электрон испускает фонон, что соответствует колебанию узлов решетки – положительных ионов. Притягиваясь к электрону, они проскакивают по инерции положения равновесия и образуют область повышенной плотности положительного заряда, которая притягивает другой электрон. Разрыв куперовской пары требует затраты энергии, поэтому куперовская пара устойчива при низкой температуре, когда тепловой энергии недостаточно для разрыва. Эффект открыл Леон Купер в 1956 г. Это стало основой теории сверхпроводимости Бардина–Купера–Шриффера. Как показывает теория, между взаимодействующими электронами расстояние , что превышает среднее расстояние между электронами проводимости или ионами решетки в 10⁴ раз. Взаимная корреляция приводит к тому, что на куперовскую пару не оказывают влияния тепловые колебания и дефекты кристаллической решетки до определенного предела. В результате сопротивление обращается в нуль и возникает сверхпроводимость.

Леон Нил Купер (1930)