Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Пределы. Сборник Матан

.pdf

Скачиваний:

141

Добавлен:

27.03.2015

Размер:

416.39 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Министерство образования и науки Российской Федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ПРЕДЕЛЫ

Сборник задач и упражнений по курсу «Математический анализ»

Составители:

канд. техн. наук, доц. С.Х. Рояк, канд. техн. наук Е.В. Чимитова, канд. техн. наук М.Г. Токарева

Рецензент канд. техн. наук, доц. Н.Д. Бекарева

Сборник задач и упражнений предназначен для студентов первого курса ФПМИ, обучающихся по направлениям 510200 – «Прикладная математика и информатика», 351500 – «Математическое обеспечение и администрирование информационных систем». Сборник содержит задачи по разделам математического анализа «Последовательности» и «Предел функции». Все задачи снабжены ответами.

Работа подготовлена на кафедре прикладной математики

2004

ОГЛАВЛЕНИЕ
1. ПОСЛЕДОВАТЕЛЬНОСТИ...................................................	4
1.1. Предел последовательности...........................................	4
1.2. Подпоследовательности. Частичные пределы по-
следовательности ...................................................................	9
1.3. Монотонные последовательности...............................	10
1.4. Фундаментальные последовательности......................	13
2. ФУНКЦИИ.............................................................................	14
2.1. Предел функции............................................................	14
2.2. Вычисление пределов показательно-степенных
функций.................................................................................	18
2.3. Сравнение функций. Символы Ландау.......................	19
2.4. Применение формулы Тейлора к вычислению пре-
делов......................................................................................	23
2.5. Правило Лопиталя.........................................................	25
Ответы...................................................................................	26
3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ.............	30
3.1. Часть 1 ............................................................................	30
Ответы...................................................................................	35
3.2. Часть 2 ............................................................................	36
Ответы...................................................................................	40
4. КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ.......................	41
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ................	46

1.ПОСЛЕДОВАТЕЛЬНОСТИ1

1.1.ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ

1.Доказать, что последовательность {xn} является ограниченной сверху. Указать наибольший член последовательности {xn} , если xn равно:

1)	21	; 2)	n	;	3) 2−n −3 4−n ; 4)	n2	.
	3n2 −14n −17
		n2 +9				2n

2. Доказать, что последовательность {xn} является ограниченной снизу. Указать наименьший член последовательности {xn} , если xn равно:

1) (2n −5)(2n −11) ; 2) n +			5		;
			n

3) log32 n −3log3 n ;	4)	1.4n		;	5)	n!	.

		n				5n

3. Доказать по определению ограниченность последовательности {xn} , если xn равно:

2n2 −1

;

1 −n

; 3)

n +(−1)n

;

n2 + 4n +8

;

3n −1

2 + n

(

)

n +1

5n6 +6

n2 +1 −n ; 7) 3 9n −n3 + 3 9n + n3 ;

; 6)

(n4 +1)(n2 −2)

3 n3 +1 −

n2 −1 ;

n4 + n3

− n2 −1 ;

10)

2n +1

;

n2 +1

3n −2

11) lg (3n +5)−lg (n +1);

12)

n +ln n

n +1

1 Буквы n, m, k используются только для обозначения натуральных чисел.

4. Доказать по определению неограниченность последовательности {xn} , если xn равно:

1) (−1)n n ; 2) n2 −n ; 3) 5n −4n ; 4) n +(−1)n n ; 5) n(−1)n ;

1 −n

; 7) (1−n)

sin(

πn / 2)

n −n4

; 8)

;

; 10)

;

n2 +1

(n + 2)3

11)

n4 + n3 +1 −

n4 −n3 +1 ;

12)

n2 +(−1)n n3 −n .

5. Указать какой-либо номер n0 , начиная с которого члены последовательности {xn} удовлетворяют заданному неравенству:

(−1)n −3

≤ 0.1 ; 2)

n +3

−1

≤ 0.01 ;

n +1

1−2n+1

+ 2

≤ 0.001 ;

4) x = n 1.5,

x −1

≤ 0.1.

1 + 2n

6. Доказать по определению, что:

lim

;

2) lim

+ 2

=1 ;

3n +1

n→∞

n→∞ n2

lim

= 0,

где

p ≥1;

lim

n→∞ n p

n→∞ 4 5n −9

lim

= 0 ;

lim

=1;

n→∞ k n

n→∞

n2 + n

lim

3n + 4

= 0 ;

8) lim

= 0,

≤1 ;

n→∞

n→∞ n

7. Доказать по определению, что:

lim (−1)n ≠ −1;

2) lim cos πn

≠

;

n→∞

lim 2(−1)n n

≠ 0 ;

4) lim 2(−1)n n ≠ ∞.

n→∞

= 0 ;

9) lim sin n = 0 . n→∞ n

8. Доказать по определению, что последовательность {xn} рас-

ходится:
1)	x = (−1)n	; 2) x = n ; 3) x = (−1)n n ;
	n	n			n
4)	x = n(−1)n	; 5) x =sin πn		;	6) x =sin n .
	n	n	2		n
			2

9. Какие из последовательностей задания 8 являются: а) ограниченными; б) бесконечно большими?

10. Доказать по определению, что {xn} – бесконечно большая последовательность:

x =

;

2) x =

;

3) x =

n +8

n 2 −1

− n n

11. Доказать по определению:

lim n =+∞ ;

lim

(−1)n n = ∞;

n→∞

lim

(5 −0.5n) = −∞ ;

lim

3 n −100 = +∞ ;

n→∞

∞,

>1;

+∞,

a >

lim

<1.

lim loga n =

−∞, 0

< a <1.

n→∞

lim nk = +∞;

lim n1/ k = +∞ .

n→∞

12. Доказать,

что последовательность {xn}

неограничена, но не

является бесконечно большой:

πn

−

x = n2 cos

;

= n(

;

x =

πn

1 + nsin 2

13. Используя

свойства

бесконечно

больших

последова-

тельностей, доказать:

lim

(2n −5)5 = +∞ ;

lim

(lg n)3

=+∞;

n→∞

lim

(loga n)k

=+∞, a >1 ;

lim (0.5 −(−1)n 3 n ) = ∞;

n→∞

lim (4

n→∞

lim

(−n)n = ∞ ;

n −n) = −∞;

n→∞

lim

(an +b) =

+∞,

a > 0;

lim

= +∞ ;

n→∞

−∞, a < 0.

n→∞ n +1

n4 +100n2

lim

= +∞ ;

10)

lim

−1

−

= +∞;

n→∞ n2 −100

n→∞

11)

lim

(

lg n + 2cos

(

πn

))

= +∞ .

n→∞

14. Даны последовательности

(−1)

n +10

Выбрать из этих бесконечно малых последовательностей такие, что:

1) lim	xn	= ∞ ;	2) lim	xn	= 0 ;	3) lim	xn	=1;

n→∞ yn			n→∞ yn			n→∞ yn

4)последовательность xn расходится, но ограничена.

Вычислить

lim x , если x

равно (15–20):

n→∞

n −1

3 +0.5n

+ 27

15.

; 2)

;

3n +

0.3n+1 +5

−15

;

2 −n

2−n n

; 7)

2n+2 +3n+3

;

5 +3n+1

n +1

n + 2

2n +3n

(n +5)3

−n(n +7)2

;

n2 +1

−

3n2

2n +1

		2n +3 n			n +10			n							1				n +1
16.	1)			;	2)			;	3)				9	+		;		4)				;
16.	1)			;	2)			;	3)				9	+		;		4)				;
		n2			2n	−1									n				n2 + 2n
5) n2−1 −n −1 ;					6) n2+ n − n2−n ;									7) 3 n3+2n2 −n ;
8)	3	n +0.25	;	9)	3 n2 + n		,	10)		n2 +1 +							n	.
8)	3	8n +1	;	9)	n + 2		,	10)	3		n	3	+ n + n					.
		8n +1			n + 2				3			3

17.	1) 3n 8 ;		2) 2n 0.5 ; 3) n2 6 ;						4)		n 10 −2						; 5)		n 2 +	1	;
17.	1) 3n 8 ;		2) 2n 0.5 ; 3) n2 6 ;						4)		1 + n 0.01						; 5)		n 2 +	n	;
											1 + n 0.01									n

6) n 5n +1 ; n +5

10)n 3 −1 ; n 9 −1

14)	n lg n	;

	n2 −1
18)	1
	(0.3)n n!

7) n

2n +5

;

8) n 2n5 +5n ; 9)

n −0.5

11)

n 8

−1

;

12)

+3n

13)

;

−1

n+1

n +3

15)

5n +lg n

;

16)

log2 (n +3)

;

n −3.5

n −1.3

; 19)

3n n +1

; 20)

3 n2 sin n!

n!+1

n +1

5n n3 + n 7 ;

n n2 + n 3n

n10 −1 ;

1 +1.1n n

(−2)n

17)(n + 2)! ;

n n

18. 1)

;

; 3)

;

n + k

n +1

;

n(n + 2)

n2 + n

(n−1)/(n+1)

;

+ 2n + 2

n +1

(1− n )/(1−n)

10)

1 n!

;

n + 2

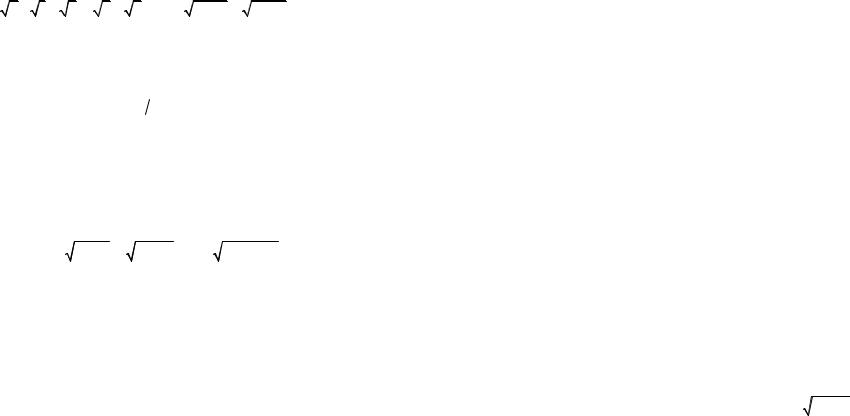
					1							1							1							n				1
19.	1)				1			+				1			+		+		1				;	2)		∑				1				;
19.	1)			1 2				+		2			3		+		+	n (n +1)					;	2)		∑		(2k		−1)(2k +		1)(2k +3)		;
				1 2						2			3					n (n +1)								k =1		(2k		−1)(2k +		1)(2k +3)
																										k =1
3)	1							1						+			1			+		+				1
																															.
		n					1	+ 3								3 +		5													.
		n					1	+ 3								3 +		5						2n −1 + 2n +1
20.	1)		12				+	22			+				+	(n −1)2			;		2)		1	+	3	+	5		+	+	2n −1		.
				n3				n3									n3						2	22			23				2n
3)				1					1									1
	1−					1−						1−									, n≥2 ;
	1−					1−			6			1−					n(n+1) 2				, n≥2 ;
				3					6								n(n+1) 2

21. Найти предел lim xn , используя теорему о трех последова-

n→∞

тельностях:

= lim

2n −1

;

n→∞

= lim

+... +

n2 +1

n→∞

+ 2

+ n +1

1.2. ПОДПОСЛЕДОВАТЕЛЬНОСТИ. ЧАСТИЧНЫЕ ПРЕДЕЛЫ ПОСЛЕДОВАТЕЛЬНОСТИ

22. Для последовательности {xn} найти все частичные преде-

lim x

, если x

лы, lim x ,

равно:

n→∞ n

n→∞

(−1)n

3) (−1)n ;

4) 3(−1)

n ;

πn

; 2)

;

5) sin

;

n +1

n +5

n cos

πn

;

−

(−1)n−1n

;

cos

πn

;

(−1)n

2n +1

;

10)

cos

2πn

n .

23. Для последовательности

}

найти

x ,

lim x

lim

sup{xn} , inf {xn}, если xn

равно:

n→∞ n

n→∞

πn +1

(−1)

1 +(−1)

3n −1

n2 sin

; 2) (−1)

;

n + 2

n +1

((−1)

−1)n

+ n +1 ;

3cos πn

−1 n +1

;

(−1)n−1

πn

n −1

2πn

2 +

; 7) 1 +

cos

;

cos

;

n +1

(−1)n n ;

10) −n(2 +(−1)n );

11) n(−1)n ;

12) 1 + nsin

πn

;

13)

n −10.2

24. Найти

lim x

, если x

равно:

lim

n→∞ n

cos

2πn

;

2) (−1)n

πn

;

sin2

πn

1 +

+sin

1 + n

1.3.МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ

25.Доказать, что последовательность {xn} монотонна, начиная

снекоторого номера и указать этот номер, если xn равно:

n +1

; 2) n3 −6n2 ; 3)

; 4) n2 + n −n ;

2n −1

n2 −

2n −100n ; 6) 3n −2n ;

7) 2n+1 −3n−2 ;

;

6n+1 −5n+1

; 10)

4n−1 +3n−1

;

11)

100n

;

6n +5n

4n +3n

12) lg (n +1)−lg n ; 13) nqn , 0 < q <1 .

26. Пользуясь теоремой Вейерштрасса о пределе монотонной и ограниченной последовательности, доказать сходимость после-

довательности {xn} :
1)	x	=		10		11					n +9				;
1)	x	=													;
	n		1			3					2n −1
			1			3			p1		2n −1					pn
2)	x	= p				+			p1		+ +					pn		.
2)	x	= p				+					+ +							.
	n		0			10									10n
						10									10n
3)	x1 = 2 , x2 = 2 + 2 , …, xn = 2 + 2 +																					2 ;
																					n корней
4)	x	=	1		−		1			1		−	1				1		−	1	;
4)	x	=	1		−					1		−					1		−		;
	n					2						4
						2						4								2n
5)	x	=	1		+			1		1		+		1			1		+	1	;
5)	x	=	1		+					1		+					1		+		;
	n					2						4
						2						4								2n

Доказать, что последовательность {xn} сходится и найти ее предел (27-33):

27.

x =

;

2) x

;

10n

(2n +1)!!

=8 ,

,…,

3n +5

1 7

6n −5

28.

> 0

;

n+1

2)xn+1 = xn (2 − xn ), 0 < x1 <1 ;

3)xn+1 = n2 xn ;

4)xn+1 = 1 2xn +125 , x1 >5 ; 3 xn2

5) x	= 2 −	1	, x = 2 .

n+1		1
		xn

29.	1) x						= k ax									,		x			= k a ,								a > 0 ;
			n+1											n					1
2)	xn+1 = 12 + xn , а) x 1=13 , б) x 1=3 ;
3)	xn+1 = 6 + xn , а) x 1=10 , б) x 1= −2 , в) x 1= 4 ;
4)	x			= 3 6 + x , x															1	=1 .
	n+1											n							1
30.	1)	x					=			4	x				− x2						, а)							x	=		1	, б)	x	=	1	, в)		x =			7	;
30.	1)	x					=				x				− x2						, а)							x	=			, б)	x	=		, в)		x =			6	;
			n+1							3 n								n										1	6				1	2				1			6
2)	x			= x2					+3x +1 , а)																x			= −		5		, б)	x	= −		7
2)	x			= x2					+3x +1 , а)																x			= −				, б)	x	= −
	n+1						n							n											1				4				1	4
																													4					4
31.	x		= 4 −						3					,		x		=			6		.
31.	x		= 4 −											,		x		=					.
	n+1								xn							1					7
									xn												7
32.	x		=1 −						1					, а)				x			>				1		, б) x					< 0 , в) 0 < x					<		1	.
32.	x		=1 −											, а)				x			>						, б) x					< 0 , в) 0 < x					<			.
	n+1							4xn											1						2				1					1				4
								4xn																	2													4
33.	1)	x					=		1 +				6				,		x				= −3 ;
33.	1)	x					=		1 +								,		x				= −3 ;
			n+1											xn						1
					1+ xn									xn											7
2)	xn+1			=	1+ xn										,	x1			= −						7		;

							2xn																	13
3)	x			=		1			−		3			,			x		=			8				.
3)	x			=					−					,			x		=							.
	n+1					xn			2							1					17
						xn			2												17

34. Используя теорему Штольца, вычислить следующие пределы:

lim

;

lim

1k + 2k +

+ nk

;

n→∞

nk +1

1k + 2k

+ + nk

−

lim

;

n→∞

k +1

lim

1k +3k +

+(2n +1)k

;

6) lim

nk+1

n→∞

3) lim d n , d >1 ; n→∞ n

1		+	1	+ +	1
	1					.
			2
n					n

35. Используя теорему Штольца, доказать, что если последовательность {an} сходится и имеет предел a , то последователь-

	a + a		2	+	a
ность		1			n	средних арифметических значений эле-
			n

ментов последовательности {an} сходится к тому же пределу a .

1.4.ФУНДАМЕНТАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ

36.Доказать, что последовательность {xn} сходится, если xn равно:

1) x

cos1

cos 2

cos n

;

2) x =

;

n +1

;

3n −2

= 0. 77...7 ;

x = a + aq +... + aqn−1, где

<1;

n штук

sin a

sin (2a)

sin (3a)

sin (na)

37. Пользуясь отрицанием условия Коши, доказать, что последовательность {xn} расходится, если xn равно:

1)	x =(−1)n	; 2)	x =1 +		1	+	1	+ +		1	;

	n		n		2	3				n
3)	x = 0.2(−1)n n ;		4)	n cos(		πn)		−1	.

	n				2n

2.ФУНКЦИИ

2.1.ПРЕДЕЛ ФУНКЦИИ

38.Нарисовать график функции f (x) , для которой:

lim f (x)

lim f

(x)

lim f (x)

(

0 )

lim

f (x)

lim

f (x)

lim f

(x)

x→−∞

x→x0 −0

x→x0

x→x0 +0

x→+∞

x→∞

–2

+∞

–1

−∞

+∞

−∞

+∞

−∞

–3

−∞

∞

−∞

+∞

∞

−∞

+∞

39. Исходя из определения предела функции по Коши, доказать:

lim (3x −8) = −5 ;

lim x2 = 4 ;

lim

x2 =9 ;

x→1

x −1

x→2

2x −1

x→−3

sin x

lim

;

lim

;

lim

= 0 ;

x→3 2(x +1)

x→+∞ 3x + 2

x→∞

lim loga x =∞, a >1 ;

lim ln x = −∞ ;

x→∞

ax = +∞, a >1 ;

x→+0

lim

10)

lim

x −1 = 0 ;

x→+∞

x→1+0

11) lim

= −∞;

12)

lim

=+∞;

x→1+0 (1 − x)3

x→1−0 (1 − x)3

13) lim

=∞;

14)

lim

arcsin x =

π ;

x→1 (1 − x)3

x→1−0

15)

→ +0 при x → +∞ ;

16)

→ −0 при x → −∞ .

40. Исходя из определения предела функции по Гейне, доказать, что предела не существует:

lim sin

;

2) lim cos

−1

x→1

x→0

41. Вычислить односторонние пределы:

lim

tg x ;

lim

tg x ;

x→π−0

x→π+0

lim

arctg

;

lim

arctg

;

1 − x

− x

x→1−0

x→1+0

lim

;

lim

;

+e1/ x

x→−0 1 +e1/ x

x→+0 1

lim

ln (1 +ex )

;

lim

ln (1 +ex )

x→−∞

x→+∞

42. Найти а)

f (−0) , б)

f (+0) :

f (x) =

x −

;

f (x) = arccos(x −1) ;

f (x) = e−1/ x2 ;

f (x) = 2ctg x .

Существует ли предел функции f (x)

в точке x0 = 0 ?

43. Найти а)

f (x0 −0) , б)

f (x0 +0) :

f (x) =

2(1− x2 )+

1− x2

, x =1 ;

3(1 − x2 )− 1− x2

2)f (x) =sgn (cos x), x0 = π2 ;

3)f (x) = arctg (tg x), x0 = π2 ;

4) f (x) =	1	,	x0 =3 .
	x +31/(3−x)

Существует ли предел функции f (x) в точке x0 ?

Вычислить предел (44-49):

44. 1)

−3x +1

3) lim

(x −1) 2 − x

lim

;

lim

+1 ;

x→2 x

−3

x→0

x −4

x→1

−1

45.

1) lim

x3 + x

;

lim

x4 −5x

;

x→∞ x4 −3x2 +

x→∞ x2 −3x +1

−1

lim

;

lim

− x ;

x→∞ 2x

1 + x

x→∞

−

3x2

−

(2x −1)(3x2 + x + 2)

lim

;

lim

;

−1

2x +1

x→∞

lim

(1 + x11 +7x13 )3

;

lim

(2x −3)20 (3x + 2)30

(1 + x4 )10

x→∞

(1 + 2x)50

46.

1) lim

(x2 − x −2)20

;

lim

x4 −3x + 2

;

x→2 (x3 −12x +16)10

x→1 x5 −4x

lim

x3 −2x2 −4x +8

;

lim

;

x4 −8x2

+16

−1

x→2

x→1 1− x3

−4x +

x −4

lim

x→1 x2

−5x +

4 3x2 −9x

47.

1) lim

1 +14x

;

lim

5x6

−1

;

2x + 3 x2

x→∞

x→∞ x12 +5x5 −1

lim

4x2 + x3 + x4

;

lim

x + 3 x +

4 x

;

x2 + 4

x→∞

lim

−3 (x −

; 6) lim

−

−1

3 (x +1)

x→∞

48.

1) а)

lim

( (x +a)(x +b) −x) ,

x→+∞

б)

lim

(

(x +a)(x +b) − x) ;

x→−∞

2) а)

lim

x2−2x−1 −

x2−7x+3

x→+∞

б)

lim

x2−2x−1 −

x2−7x+3 .

x→−∞

49.

lim

1 + 2x −3

;

2) lim

x3 −

;

x −2

x −

x→4

x→1

lim

3 x −6 + 2

; 4)

lim

1 −

3 x

5 x

x→−2

x→11 −

Используя замечательные пределы и их следствия, вычислить

(50–52):

50.

lim

sin 5x

;

lim

1 −cos 2x

;

3) lim

x ctg

(

))

;

x→0

x→0 (

2arcsin x

−

lim

;

lim

;

lim

;

1 + x

x→0

x→∞

lim

1 + x −1

;

lim

;

lim

3 1 + x − 3 1− x

x→0

x→0 5

1 +3x −1

x→0

51.

lim

sin (mx)

;

2) lim

sin(πxα)

;

lim

ex −e2x

;

x→π sin (nx)

x→1 sin(πxβ)

x→0

sin x

4) lim

1 − x2

; 5) lim

(1 − x) tg πx

; 6) lim

(

2x) tg π

− x

;

x→1

ln x

x→1

x→π

lim

tg x −sin x

;

8) lim

cos x −cos3x

;

lim

sin x −sin a

;

x −a

x→0

sin3 x

x→0

ln x −ln a

x→a

10)

lim

x(ln(x +1) −ln x) ;

11)

lim

, a > 0 ;

x −a

x→+∞

x→a

12)

lim

ln (x2 − x +1)

;

13)

lim

lg(x + h) +lg(x −h) −2lg x

;

x→+∞ ln(x10 + x +1)

h→0

14)

1 + x / 3 − 4 1+ x / 4

15)

1 + x − 1− x

lim

;

lim

;

1 − 1− x / 2

3 1 + x − 3

1− x

x→0

m 1 +αx − n 1+βx

ax+h + ax−h −2ax

52.

1) lim

;

lim

, a > 0 ;

x→0

h→0

lim

xα

−aα

, a >

0 ;

lim

sin(a + 2x) −2sin(a + x) +sin a

;

−aβ

x→a xβ

x→0

lim

2sin2 x +sin x −1

;

lim

1 + tg x −

1+sin x

;

x→π/ 6 2sin2 x −3sin x +1

x→0

lim

;

lim

sin2

(π2x )

;

(cos(π2x ))

x→0 1

+ xsin x −

cos x

x→1 ln

(n a −n+1 a ), a > 0 ;

cos 2π

− x

lim n2

10)

lim

n→∞

x→π/ 6

3 −2cos x

2.2. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ ПОКАЗАТЕЛЬНО-СТЕПЕННЫХ ФУНКЦИЙ

Вычислить (53–54):

x +1

1− x

x +1

1− x

53. 1) lim

1−x

;

lim

1−x

;

x→0

x + 2

x→1 x + 2

3) lim x + 2 x2

x→∞ 2x −1

6) lim x +a x ; x→∞ x −a

x2 +2

;

lim

;

lim

;

−2

x→∞ x

x→0 x

−1

x2 −1

1/ x

lim

;

lim

;

x→0 x2 + x −2

x→0 x2

+ x −2

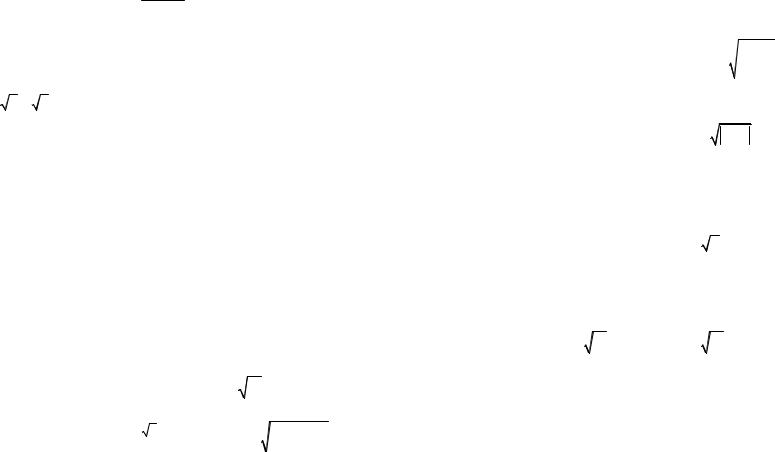
9)		x2 −1	x
	lim		;

x→∞ x		2 + x −2
11)	xlim→0 (1 + x2 )ctg2x ;
13)	lim	(sin x)tg x ;
	x→π/ 2

10)			x2 −	1		1/ x
	lim								;

	x→∞ x2 + x			−2
		tg x +1			1
							3	x
12)	lim			sin					;

	x→0	sin x +1

14) lim a1x +b1 x , a1 >0,a2 >0 . x→∞ a2x +b2

54.

1) lim

(x +a)x+a (x +b)x+b

, a > 0,b > 0 ;

(x +a +b)2x+a+b

x→∞

n a

+n b

lim

, a > 0,b > 0 ;

n→∞

ax+1 +bx+1 +cx+1 x

lim

, a > 0,b

> 0,c > 0 ;

a +b +c

x→0

x2 x

lim

, a > 0,b > 0 .

x→0

2.3. СРАВНЕНИЕ ФУНКЦИЙ. СИМВОЛЫ ЛАНДАУ

55. Установить, какие из следующих устверждений верны при

x →0 :
1) α(x) = o(x2 ) ;	2) α(x) = o(x) ;	3) α(x) =O(x);
4) α(x) =O(x2 ) ;	5) α(x) x3 ;	6) α(x)	x	,
4) α(x) =O(x2 ) ;	5) α(x) x3 ;	6) α(x)	x	,
если:	б) α(x) = e x −1 , в) α(x) = ln (1+ x3 ) ,
а) α(x) =sin x3 ,	б) α(x) = e x −1 , в) α(x) = ln (1+ x3 ) ,
г) α(x) = x2 + x3 ,	д) α(x) = x sin x .
	19

56.Установить, какие из следующих устверждений верны при

x→∞ :

1) α(x) = o

;

α(x) = o sin

;

3) α(x) =O

;

6) α(x) =

α(x) =O

;

α(x) =

;

2x3

если:

а) α(x) =3 tg

, б)

α(x) =3

−

, в) α(x) = x−3/ 2 ,

−4

г) α(x) = x

2 ex

−1

, д) α(x) = 1 +

57.Установить, какие из следующих устверждений верны при

x→1:

1) α(x) = o(x −1); 2) α(x) = o( x −1 ) ;

3) α(x) =O((x −1)2 ) ; 4) α(x) =O((x −1)3 );

5) α(x) (x −1) ; 6) α(x) (x −1)2 ,

если:

б) α(x) =( x −1)2 , в) α(x) = e(x−1)2 −1,

а) α(x) = ln x ,

г) α(x) = ex−1 −cos (x −1),

д) α(x) = o((x −1)2 ).

58. Верно ли утверждение x3 = o(β)

при x →0 , если:

а)

β(x) = x2

;

б) β(x) = x3

;

в) β(x) = x2 sin x .

г)

β(x) =1−cos x2 ; д) β(x) = ln (1+sin x4 ) ; е) β(x) = etg x .

59. Верно ли утверждение (x −1)2 = o(β) при x →1, если:

а)

β(x)=(x−1)3 ;

б) β(x)=sin (x−1)2 ; в) β(x) =(x −1)2 / ln x .

г)

β(x) = cos(x −1)2 ; д) β(x) = e(x−1)4 −1 ; е) β(x) = ln x .

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.12.2018721.41 Кб21ПРАВОО Леонова.doc
#
27.03.201592.04 Кб21правообеспечение.docx
#
11.03.20161.28 Mб12Практика 1.pdf
#
24.11.20191.16 Mб63практикум по логистике.doc
#
15.11.2019670.72 Кб19ПРАКТИКУМ ПО КОНФЛИКТОЛОГИИ.doc
#
27.03.2015416.39 Кб141Пределы. Сборник Матан.pdf
#
16.04.2019299.45 Кб35Предмет методологии -экз.docx
#
27.03.20153.64 Mб7ПРЕЗЕНТАЦИЯ ЕДОША-ГУРМАНЫ ОБЩАЯ 02.12.13.pdf
#
17.07.2019139.47 Кб9При потомках Дмитрия Донского Русское государст....docx
#
04.09.2019822.78 Кб3Приложение к законам сохранения.doc
#
02.05.2019319.49 Кб2Пример задания по мат.стат.2 2008.doc