5.3 Сходимость по вероятности

Это сходимость последовательности случайных величин Х 1, Х 2, . . ., Х n, . . ., заданных на нек-ром вероятностном пространствек случайной величине X, определяемая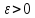 следующим образом:

если для любого

P

5.4 Закон больших числе в форме Чебышёва

Пусть последовательность Х 1, Х 2, . . ., Х n, . . случайных величин удовлетворяет закону больших чисел, если для любого

Иными словами, выполнение закона больших чисел отражает предельную устойчивость средних арифметических случайных величин: при большом числе испытаний они практически перестают быть случайными и совпадают со ссвоими средними значениями.

Последовательность Х 1, Х 2, . . ., Х n, . . удовлетворяет закону больших чисел тогда и только тогда, когда среднее арифметическое случайных величин X₁-m₁ Х₂-m₂, . . ., Х_n-m_n сходятся по вероятности к нулю при

5.5 Закон больших чисел в форме Бернулли (схема Бернулли)

Пусть производится последовательность независимых испытаний, в результате каждого из которых может наступить или не наступить событие А, причем вероятность наступления этого события одна и та же при каждом испытании и равна р. Если событие А фактически произошло m раз в n испытаниях, то отношение m/n называют, как мы знаем, частотой появления события А. Частота есть случайная величина, причем вероятность того, что частота принимает значение m/n, выражается по формуле Бернулли

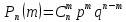
Закон больших чисел в форме Бернулли состоит в следующем: с вероятностью, сколь угодно близкой к единице, можно утверждать, что при достаточно большом числе опытов частота появления события А как угодно мало отличается от его вероятности, т. е. иными словами, при неограниченном увеличении числа n опытов частота m/n события А сходится по вероятности к Р(А).

5.6 Центральная предельная теорема (формулировка, пример применения для решения задач)

Закон распределения суммы независимых случайных величин _{Xi(i=1,2,…,n) приближается} к нормальному закону распределения при неограниченном увеличении n, если выполняются следующие условия:

1) все величины имеют конечные математические ожидания и дисперсии:

2) ни одна из величин по значению резко не отличается от остальных:

5.7 Центральная предельная теорема в случае схемы Бернулли (теорема Муавра-Лапласа).

Если вероятность p наступления события A в каждом испытании

постоянна и отлична от нуля и единицы, а число независимых испытаний

достаточно велико, то вероятность можно вычислять по приближённой

формуле:

(тем точнее, чем больше n)

Глава 1. Случайные события

1. Случайные события: элементарные, достоверные, невозможные, несовместные, совместные, равновозможные. Попарно-несовместные, образующие полную группу. Пространство элементарных событий. Случай.

2. Сумма, произведение, разность, отрицание. Теоретико-множественная трактовка. Диаграммы Эйлера-Венна. Алгебра событий. Понятие сигма-алгебры.

3. Частота события. Свойство статистической устойчивости. Статистическое определение вероятности.

4. Классическое определение вероятности события. Непосредственное вычисление вероятностей.

5. Комбинаторика: правило умножения и сложения. Основные схемы: с возвращением, без возвращения. Понятия размещения, сочетания, перестановки.

6. Геометрическое определение вероятности.

7. Аксиоматическое определение вероятности. Свойства вероятностей.

8. Вероятностное пространство.

9. Условная вероятность.

10. Вероятность произведения событий.

11. Независимость событий.

12. Вероятность суммы событий.

13. Формула полной вероятности.

14. Формула Байеса.

15. Понятие простой однородной цепи Маркова.

16. Независимые испытания. Схема Бернулли. Формула Бернулли. Многоугольник распределения вероятностей.

17. Предельные теоремы в схеме Бернулли: формула Пуассона, локальная и интегральная теоремы Муавра-Лапласа.

18. Схема Бернулли. Наивероятнейшее число.