Распределение по модулю скорости

Интегрируем (2.43) по углам, учитываем :

(2.44)

– вероятность обнаружения частицы с модулем скорости от v до ,

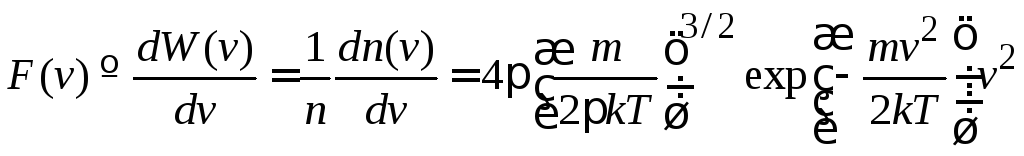(2.44а)

– функция распределения по модулю скорости – относительное число частиц с модулем скорости в единичном интервале около ;

dn(v) – концентрация частиц с модулем скорости от v до ;

–концентрация частиц с модулем скорости в единичном интервале около v.

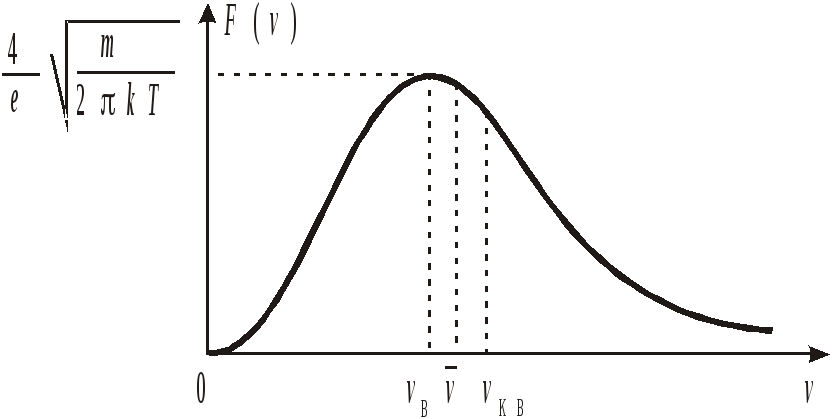
Условие нормировки

,

площадь под кривой – единица;

с ростом Т максимум понижается, сдвигается вправо и увеличивается вероятность обнаружить частицу с большей скоростью.

Наиболее вероятная скорость

,

.

Из (2.44а)

находим

(2.45)

Средняя скорость

.

Подставляем

, (2.44а)

находим

. (2.46)

Доказательство:

,

,

, , .

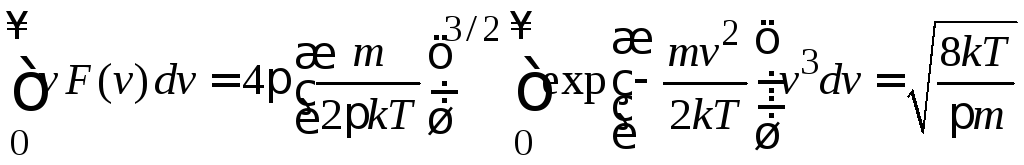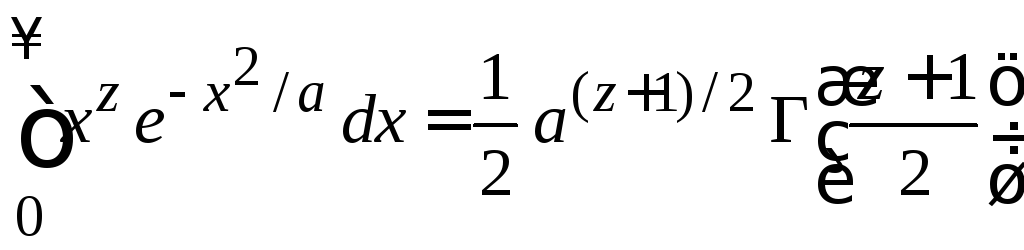Средняя квадратичная скорость

.

Подставляем (2.44а)

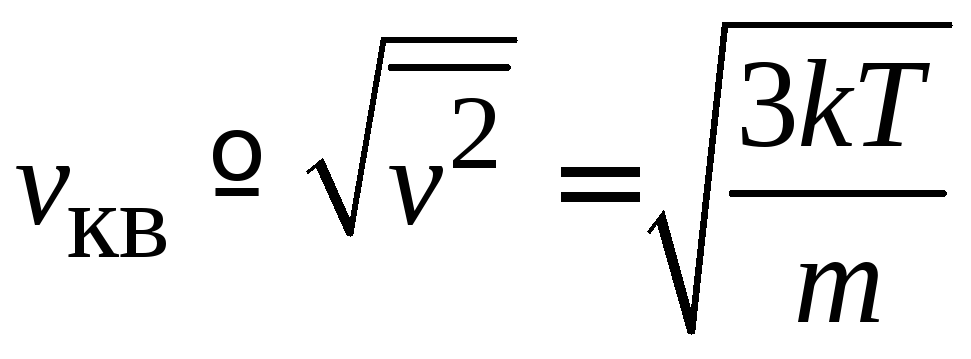. (2.47)

Распределение по энергии

Заменяем

, ,,

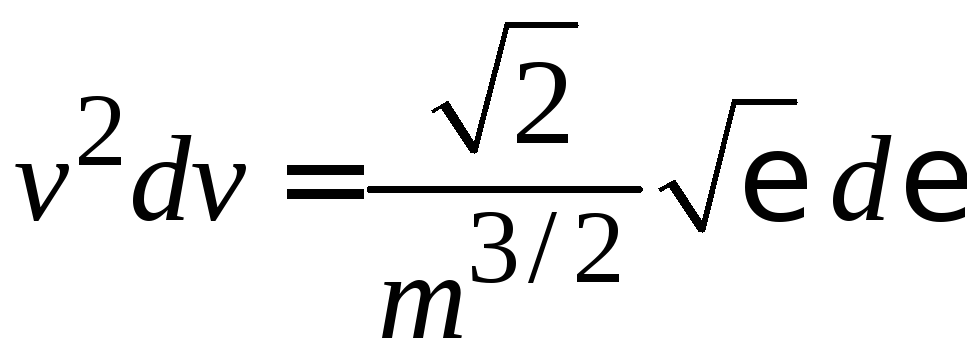в распределении по модулю скорости (2.44)

получаем

(2.48)

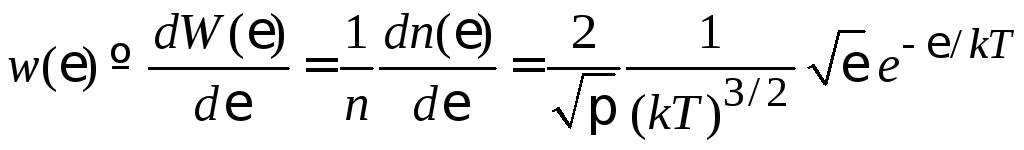, (2.48а)

– распределение Максвелла по энергии – относительное число частиц с энергией в единичном интервале около ;

–концентрация частиц с энергией от ε до e + de;

–концентрация частиц с энергией в единичном интервале около .

Нормировка

.

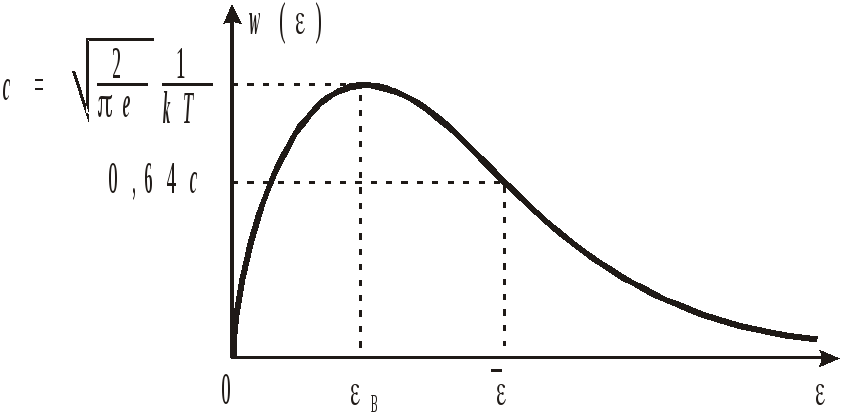
Площадь под кривой – единица;

с ростом Т максимум понижается, сдвигается вправо и увеличивается вероятность обнаружить частицу с большей энергией.

Наиболее вероятная энергия

.

Из (2.48а)

получаем

. (2.49)

Средняя энергия

(2.50)

согласуется с теоремой (2.39) о распределении кинетической энергии по степеням свободы. При получаем.

Доказательство (2.50):

Используем

, (2.48а)

находим

,

,

, , .

Плотность потока частиц по оси z

–среднее число частиц, проходящих за 1с через единичную площадку, перпендикулярную к оси.

Движения по x и y не влияют на результат, поэтому считаем эти скорости нулевыми.

Проходящие за 1с частицы с проекцией скорости заполняют в начальный момент цилиндр с единичным основанием, с образующей вдоль осиz длиной . Концентрация таких частиц. Через 1с все эти частицы пересекут правое основание цилиндра, их число .

Суммируем по всем скоростям с положительной проекцией и получаем

.

Используем (2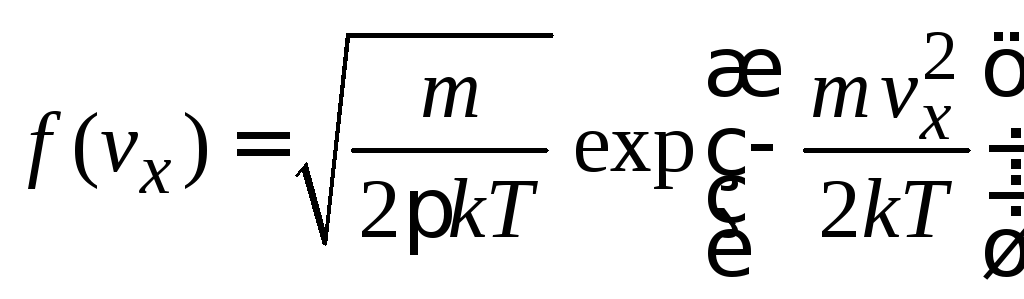.42а)

,

, (2.42а)

тогда

. (2.51)

Вычисляем интеграл

,

,

, , ,

получаем

(2.52)

– плотность потока частиц – число соударений частиц со стенкой единичной площади за 1 с,

учтено

. (2.46)

Плотность потока импульса

–средний импульс, переносимый за 1с через единичную площадку, перпендикулярную оси z.

Частица несет импульс ,

число таких частиц со скоростями равно

,

тогда

. (2.53)

Доказательство:

,

,

, , .