Примеры динамического хáоса

, f – нелинейная функция,  – параметр.

Когда при изменении параметра  существует периодическое решение с периодом Т:

t1, t2, t3 – точки бифуркации

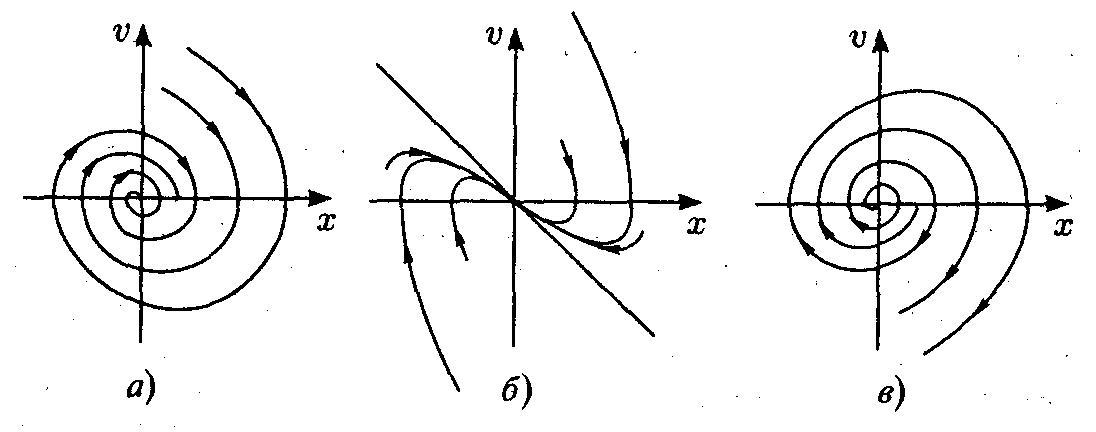
Фазовые портреты линейного осциллятора: а) устойчивый фокус; б) узел; в) неустойчивый фокус. Узел и фокус – примеры аттракторов

Теория автоматов

АВТОМАТ – устройство или управляющая система, дискретный преобразователь множества его входных сигналов (внешних воздействий) А в непустое множество М его внутренних состояний и множество ответов – выходных сигналов В по функциям переходов  и выходов .

А – входной алфавит; В – выходной алфавит. Автомат описывается множеством М состояний, начальным состоянием и правилами перехода из состояния в состояние.

ВИДЫ АВТОМАТОВ:

Конечные (М-конечное), бесконечные;

Детерминированные (-детерминированные функции), индетерминированные;

Клеточные (состояния отображаются клетками), табличные, графовые и т.п.

а) б)

Вход

А1

А2

…

Аn

состояние

Вход

А1

…

Аn

1

Выход

В1

В2

…

Вn

М1

M1,1

…

M1,n

М2

M2,1

…

M2,n

k

Мk

Mk,1

Mk,n

Клеточный Табличные автоматы Графовый автомат

автомат

Задачи теории автоматов:

1. Анализа: – по заданному автомату описать его поведение или по неполным данным об автомате и его функционированию установить его свойства.

2. Синтеза – построение автомата с наперед заданными структурой, свойствами, поведением или функционированием.

3. Полноты – выяснить, обладает ли подмножество автоматов свойством полноты – совпадает ли смножество всех автоматов, которые получаются путем конечного числа применений некоторых операций к автоматам из.

4. Эквивалентных преобразований – найти полную систему правил преобразований автоматов, удовлетворяющих определенным условиям и позволяющих преобразовать произвольный автомат в любой эквивалентный ему (имеющий одинаковое поведение) автомат.

5. Минимизации – числа состояний автомата, сохраняющих его поведение.

1 Способные поддерживать свою целостность в процессе функционирования и взаимодействия с окружающей средой

1 Теория вероятностей – раздел математики, связанный с введением и изучением вероятностных моделей, их свойств, характеристик, преобразований.

1 Математическая статистика – раздел математики, связанный с построением и изучением статистических моделей, их разновидностей, свойств, характеристик по значениям случайных элементов (величин, векторов, функций), полученных в четко определенных (идеализированных) условиях.

2 Прикладная статистика – раздел математической статистики, направленный на работу со значениями в условиях, отличных от идеализированных, приближенных к реальным.

1 Ярушкина Н.Г. Основы теории нечетких и гибридных систем. – М.: Финансы и статистика, 2004. – 320 с. (С. 24–25).

32