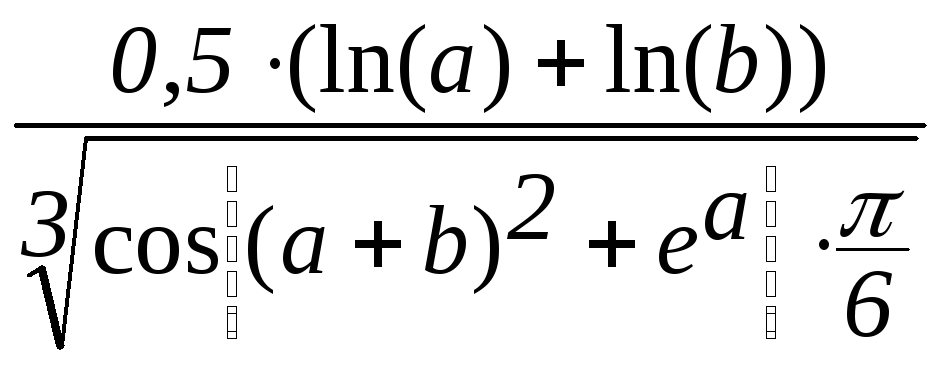Лабораторная работа №2 Линейные, разветвляющиеся, циклические и итерационные алгоритмы

Задание 1. Научиться вычислениям по сложным формулам с использовани­ем математических функций, используя линейный алгоритм.

Задача. Вычислить значения функции y = f(a, b) для заданных a и b по вариантам, приведенным в табл. 1.

Методические указания:

1. Значения а, b для тестирования подобрать таким образом, чтобы значение y и все промежуточные значения легко проверялись.

2. Вычисление y производить посредством не менее чем трех операторов с получением промежуточных значений.

Задание 2. Научиться реализовывать разветвляющиеся алгоритмы.

Задача. Вычислить значение функции f(t) при заданных a, b, n, если значение аргумента t изменяется от t_min = a до t_max = b с шагом t = (b-a)/(n-1) по вариантам в табл. 2.

Методические указания:

1. Для реализации ветвления использовать логическую функцию «Если».

2. При реализации вычислений в формуле использовать для хранения значений a и b именованные ячейки.

Задание 3. Научиться использовать итерационные циклические структуры.

Задача. Вычислить значение функции f(x) по вариантам табл. 3, используя для вычисления приближенные выражения (см. Табл. 4) с точностью =0,1. Суммирование членов ряда прекратить, если очередной член ряда, прибавляемый к сумме, будет меньше .

Методические указания:

1. В одном из столбцов поместить значения a.

2. Для реализации ветвления использовать логическую функцию «Если».

Задание 4. Научиться вычислять значение определенного интеграла с использованием приближенного метода трапеций.

Таблица 1

Номер варианта		Значения
		а	в
1		4	0,5
2		2	14,36
3		10	0,5
4		2	11,05
5		3	0,151
6		4	1,310
7		2	200,0

Продолжение табл.1

8		1	12,21
9		3	0,521
10		2	12,11
11		1	20,01
12		3	0,707
13		3	2,712
14		2	19,03
15		4	300,1
16		3	0,501
17		2	13,13
18		1	0,001
19		4	0,707
20		1	1,201

Продолжение табл.1

21		2	13,17
22		2	3,141
23		4	3,141
24		1	15,15
25		3	0,523

Таблица 2

№ Варианта	f(t)	Значения
		а	b	n
1	f(t)=	-		51
2	-1 f(t)= t 1	-3	3	51
3	f(t)=			41
4	1 f(t)= 0 -1			41

Продолжение табл.2

5	f(t)=				51
6	1-t f(t)= 1 1+t	0	5		51
7	f(t)=				61
8	f(t)=	0	10	61
9	f (t)=			66
10	f(t)=	0	10	66
11	f(t)=			41
12	f(t)=	0	3	41
13	f(t)=	0		61
14	f(t)= 1	0	5	61
15	f(t)=			51

Продолжение табл.2

16	f(t)=	0	20		51
17	f (t)=				41
18	f (t)=	0		15	41
19	f(t)=				51
20	f(t)=	0		2	51
21	f(t)=	2		10	41
22	f (t)=				56
23	f(t)=	5		15	56
24	f(t)=	3		11	61
25	f(t)=	-1		1	61

Задача. В рабочем листе вычислить значение определенного интеграла по формуле:

,

где t = (q-p)/(n-1).

Аналитические выражения функций f(t) приведены в табл. 5.

Методические указания:

1. Построить значения подынтегральной функции f(t).

2. Построить график f(t).

3. Используя график, выбрать пределы интегрирования a и b.